 |
Понятие и основные этапы изучения связи явлений. Виды связей и зависимостей признаков
|
|
|
|
Базисные и цепные индексы.
Часто в ходе экономического анализа изменение индексируемых величин изучают не за два, а за ряд последовательных периодов. Следовательно, возникает необходимость построения индексов за ряд этих последовательных периодов, которые образуют индексные системы. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.
В зависимости от базы сравнения индексы бывают базисными и цепными.
В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.
Цепные и базисные индексы могут быть как индивидуальные, так и общие.
Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода подстрочными значениями 0, 1,2, 3, исчисляем базисные и цепные индивидуальные индексы цен:
· базисные индексы:  ;
;  ;
; 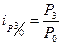 ;
;
· цепные индексы:  ;
;  ;
;  .
.
Между цепными и базисными индивидуальными индексами существует взаимосвязь, позволяющая переходить от одних индексов к другим — произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода:
 .
.
Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:
 ;
; 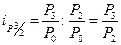 .
.
Гармонический индекс
Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.
|
|
|
Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:

Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.
Агрегатный индекс физического объема.
Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.
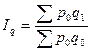
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.
Разность числителя и знаменателя (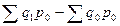 ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.
Агрегатный индекс ФОП (предложен Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р:

где q1 и q0 - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p0 - цена единицы продукции (отдельного вида) в базисном периоде.
При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость.
Понятие и основные этапы изучения связи явлений. Виды связей и зависимостей признаков
В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы, оказывающие основное влияние на вариацию изучаемых процессов и явлений.
Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины – ведет к изменению другого – следствия.
|
|
|
Причина – совокупность условий, обстоятельств, действия которых приводит к появлению следствия. Причинные связи носят всеобщий многообразный характер. Для обнаружения причинно-следственных связей необходимо отбирать отдельные явления и изучать их изолированно.
Особенностью причинно-следственных связей является их транзитивность, т.е. причина x и следствие y связаны следующим образом
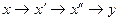
Статистическое изучение связей состоит из этапов:
1) качественный анализ изучаемого явления
2) построение модели связи (методы статистики)
3) интерпретация полученных результатов.
В статистике по степени тесноты различают функциональную связь и стохастическую зависимость. Функциональной называют связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменении среднего значения результативного признака обусловлено изменением факторных признаков.
По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются под воздействие факторного в противоположном направлении по сравнению с изменением факторного признака.
По аналитическому выражению выделяют связи прямолинейные и нелинейные.
Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии – то нелинейной или криволинейной.
|
|
|


