Магнитомеханические явления.

 

Твёрдое вещество можно рассматривать и как механическую систему, состоящую из узловых точек кристаллической решетки, вокруг которых происходит вращение электронов. Если все силы и механические моменты, действующие на вещество уравновешены, то такая система находится в состоянии покоя, центр масс системы находится в строго определённой точке. Вследствие вращения электронов атомы вещества обладают моментом количества движения . В общем случае можно принять, что и ядра атомов имеют момент количества движения . Направление этих моментов устанавливается таким образом, что итоговый момент количества движении всего вещества равен нулю, что соответствует закону сохранения момента количества движения, поэтому выполняется условие

 

, (1.17)

 

где N -число электронных орбит; K -число ядер атомов.

В магнитном поле магнитные моменты атомов устанавливаются вдоль направления магнитного поля, а механические моменты в противоположном направлении, поэтому они изменят свое первоначальное положение. Первое слагаемое в выражении (1.17) изменяет свое значение, следовательно, изменит свое значение и второе слагаемое, таким образом, что итоговый момент количества движения останется равным нулю. Это означает, в целом вещество будет подвергнуто вращению, причём так, что изменение направления магнитного поля приведет к изменению направления вращения. Опыты, подтверждающие такое явление были впервые проведены Эйнштейном, де Хаасом, Барнетом [ ]. В ходе опытов удалось подтвердить не только гипотезу о наличии в веществах орбитальных магнитных и механических моментов электронов, но и гипотезу о наличии у электрона спина, т.е. собственного магнитного и механического моментов. Подтверждено было и то, что спином обладают не только электроны, но ядра атомов, а также другие элементарные частицы. Поскольку вещества состоят из молекул, то и молекулы обладают магнитным моментом.

Таким образом, намагничивание или размагничивание веществ под действием магнитного поля обусловлено ориентацией магнитных моментов атомов или молекул.

Поскольку вещество можно рассматривать как совокупность магнитных контуров, образованных атомами или молекулами, представляет интерес определения сил, действующих на вещество, помещённое в магнитное поле. Ответ на такой вопрос можно получить после расчета картины магнитного поля в каждом конкретном случае. Однако при равномерном распределении индукции можно использовать закон Ампера, согласно которому, на элементарный проводник с током, длиной dl в магнитном поле действует сила, определяемая в соответствии с векторным произведением

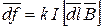(1.18)

где k - коэффициент пропорциональности, I -сила тока, B -магнитная индукция в том месте, где находится элемент тока.

Величина силы определяется по формуле

df=k I B dl Sin a, (1.19 )

где a - угол между векторами dl и B.

Направлена сила перпендикулярно к плоскости, в которой лежат векторы dl и B. Направление силы, действующей на ток, удобно определять с помощью мнемонического «правила левой руки». Если расположить левую руку так, чтобы вектор В «вонзался» в ладонь, а четыре сложенные вместе пальца были направлены вдоль тока, то отставленный в сторону большой палец укажет направление силы.

Закон Ампера иллюстрируется при вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых проводников с токами I₁ и I₂, расположенных на удалении друг от друга равном b. Напряженность магнитного поля создаваемого током I₁ на указанном удалении составит H₁=I₁/ 2 p b. Магнитная индукция этого поля равна

(1.20)

Следовательно, сила, действующая на элемент тока I₂ равна

(1.21)

Для силы f_{1_2} получается аналогичное выражение. С помощью правила левой руки легко установить, что при одинаковом направлении токов они притягивают друг друга, а при различном – отталкивают.

Пусть прямоугольный плоский контур с током размещён в однородном магнитном поле (рис 1.2). В общем виде целесообразно считать, что вектор индукции магнитного поля имеет 3 составляющих B_X,B_Y,В_Z. Если B_X ¹ 0, а B_Y =0 и В_Z =0, то в

 

Рис 1.2 Механические силы в прямоугольном магнитном контуре

 

сторонах контура согласно закона Ампера будут действовать механические силы f_X, f_X ', которые будут сжимать контур. Если направление вектора В_Х изменить на противоположное, то силы f_X,f_X' также изменят свое направление, и контур будет подвергаться растяжению. В том случае, когда контур ориентирован так, что вектор индукциирасположен вего плоскости (B_X =0, B_У ¹ 0 B_Z ¹ 0), то контур будет испытывать действия пар сил f_Y-f_Y',f_Z-f_Z'. Механический момент, создаваемый указанными парами сил можно определить в соответствии с законом Ампера. На левый участок будет согласно закону Ампера действовать сила f_Y=IВ_Y a, на правый участок — такая же по величине, но противоположно направленная сила f_Y ' (рис 1.2). Эти силы образуют вращающий момент вокруг оси Z - M_Z, который равен

M_Z=f_Y b=IB_Y ab (1.22)

Учитывая, что a · b равно площади контура S, а I · S дает величину магнитного момента контура P, можно написать

M_Z=P B_Y. (1.23)

 

Аналогично определяется момент вокруг оси Y-M_Y

M_Y=P B_Z (1.24)

 

Тогда полный момент, действующий на контур, с учётом (1.23) и (1.24) будет равен

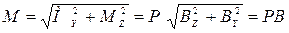(1.25)

 

Можно показать, что (1.25) справедливо и для случая, когда все 3 составляющих вектора индукции отличны от нуля. Кроме этого, (1.25) будет справедливо и для контура тока произвольной формы [ ].

Вследствие того, что происходит поворот контура с током, совершается работа. Пусть a -уголмежду вектором магнитной индукции В и направлением магнитного момента P. Тогда, чтобы этот угол увеличить на da, нужно совершить против сил, действующих на контур в поле, работу

dA=Mda=PB Sina da (1.26)

Поворачиваясь в первоначальное положение, контур может возвратить затраченную работу, совершив её над какими-нибудь телами. Следовательно, работа (1.26) идёт на увеличение энергии W, которой обладает контур с током в магнитном поле

dW= PB Sina da. (1.27)

Интегрируя, находим, что

W= -PBCosa (1.28)

Следовательно, энергия вещества, как совокупности магнитных контуров, в магнитном поле также будет увеличиваться, и оно будет способно совершать работу над другими телами. В этом заключается основное представление о преобразовании энергии в электромеханических устройствах.

Несмотря на достаточно простое толкование о преобразовании энергии, учёные не сразу пришли к такому выводу. Например, Фарадей трактовал все явления, происходящие в магнитном поле как следствие особых свойств магнитного потока и составляющих его единичных трубок магнитной индукции или совокупности физически существующих магнитных линий. С их помощью имеется возможность качественно и количественно характеризовать магнитное поле. Например, магнитное поле в поперечном сечении кругового магнитного контура представленное в виде магнитных силовых линий, изображено на рис 1.3.

По Фарадею, магнитные линии ведут себя как упругие нити, стремящиеся сократиться. Это проявляется, в стремлении сблизить элементы магнитной цепи. Вообще, во многих случаях, когда в результате существования магнитного поля возникают механические силы, их можно отнести за счет стремления магнитных линий к сокращению.

Максвелл, подвергший тщательному математическому обследованию все свойства магнитного потока, показал путем анализа и в полном согласии с воззрениями Фарадея, что в магнитном поле должны возникать механические напряжения, которые должны производить соответствующие механические воздействия на все материальные тела, внесенные в поле.

 

Рис 1.3 Магнитное поле в поперечном сечении кругового контура с током.

 

Иллюстрация указанных положений часто выполняется на примере определения силы притяжения двух разноименных полюсов, магнитное поле которых в виде магнитных силовых линий представлено на рис 1.4. В центральной части зазора поле является практически однородным. По бокам однородность поля нарушается. Для того, чтобы учесть искривление магнитных силовых линий по бокам рассмотрим только среднюю часть пространства между полюсами. Вырезанная часть представится в виде цилиндра с поперечным сечением S_m.

В силу своей упругости, магнитные линии будут стягивать полюсы, и вырезанный элемент магнита будет находиться под действием сил тяжения.

Обозначим через dF силу тяжения, дёйствующую на единицу поверхности, а через F —силу, действующую на всю площадку S_m. Тогда:

F= S_m dF (1.29)

 

 

 

Рис 1.4 Магнитное поле между полюсами магнита.

 

Под действием этой силы зазор между полюсами несколько уменьшится. Это элементарно малое смещение обозначим через dl (смещение показано на рис. 1.4 пунктиром). Такое смещение вызовет соответствующее изменение количества энергии, запасенной в магнитном поле, так как работа перемещения за отсутствием других источников энергии может быть произведена, лишь за счет энергии магнитного потока. Действительно, объем поля в пространстве между магнитами стал меньше, и количество энергии, запасенной в поле, должно соответственно уменьшиться.

Полный объем, занимаемый полем между магнитами, выражается произведением lS_m где l есть расстояние между полюсами. Считая запас энергии на единицу объема равным

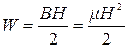, (1.30)

и пренебрегая бесконечно малыми высших порядков, получим, что, при перемещении цилиндра на элемент dl, в механическую работу превратится часть энергии магнитного поля, равная,

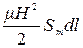(1.31)

 

С другой стороны, эта же работа равна

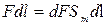(1.32)

На основании закона сохранения энергии, можно получить, что

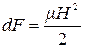(1.33)

т.е, сила тяжения магнитных линий, рассчитанная на единицу поверхности, нормальной к поверхности потока, численно равна количеству энергии магнитного поля, рассчитанному на единицу объема.

Исходя из положения, что магнитные линии ведут себя как упругие нити, естественно заключить — как это сделал Фарадей и математически обосновал Максвелл, — что такая же сила тяжения имеет место в любом сечении перпендикулярном направлению магнитного поля и, следовательно, направлению векторов магнитной индукции. Необходимо иметь в виду, что полученное выражение (1.33) пригодно лишь для однородной и изотропной среды, когда m=const. При несоблюдении этих условий, характер явления в основном остается тем же, но математическая формулировка соответствующих зависимостей значительно усложняется.

В этой и предыдущих формулах может обратить на себя внимание парадоксальный, на первый взгляд, факт, что выражения для силы и для энергии как бы совпадают между собой. Кажущаяся парадоксальность исчезнет, если учесть, что в формулах (1.31) и (1.32) фигурируют сила, рассчитанная на единицу поверхности, и энергия, рассчитанная на единицу объема. Не трудно убедиться, что при этих условиях размерности той и другой величины совпадают.

Объяснение механических действий магнитного поля тяжением магнитных линий предоставляет возможность дать весьма простое физическое толкование причин возникновения электромагнитной силы, т. е. силы механического взаимодействия проводника, несущего ток, с магнитным полем.

Рассмотрим магнитное поле между двумя полюсами магнита и помещенный в это поле перпендикулярно к нему проводник, по которому течет ток (рис 1.5).

Поскольку при прохождении по проводнику тока вокруг него возникает магнитное поле в виде кольцевых магнитных линий, то направление этого поля тока легко определяется по правилу правого винта. Картина результирующего магнитного поля может быть получена аналитически или используя численные методы.

Не трудно убедиться, что слева от проводника, как бы в силу наложения противоположных магнитных состояний среды, магнитное поле ослабится, в то время как по другую сторону проводника, наоборот, магнитные линии расположатся более густо. Поле тока, таким образом, исказит основное магнитное поле. В результате получится картина, представленная на рисунке 1.5. Там же показано распределение индукции и направление выталкивающей силы F.

Рис 1.5. Проводник с током между полюсами магнита

Аналогичные явления, в виде искажений симметрий магнитного поля токами, происходят в электрических машинах. Однако это целесообразно рассматривать совместно с расчётами магнитного поля в каждом конкретном случае, что не является целью данного пособия.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: