Банковские задачи на вклады

ЗАДАНИЕ 17 ЕГЭ.

ФИНАНСОВАЯ МАТЕМАТИКА. ВКЛАДЫ

 

БАНКОВСКИЕ ЗАДАЧИ НА ВКЛАДЫ

 

1.1. Нахождение срока вклада.

1.2. Вычисление процентной ставки по вкладу.

1.3. Нахождение суммы вклада.

1.4. Нахождение ежегодной суммы пополнения вклада.

1.5. Нахождение прибыли от вклада.

 

Разберём задачи на вклады. Обычно встречаются задачи на вклады двух типов: без ежегодного взноса определённой суммы и с внесением такой суммы.

Для определённости введём обозначения, используемые при решении задач.

 – сумма первоначального вклада.

– сумма ежегодного вклада (часто ).

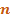– временной промежуток (количество месяцев, лет).

 – сумма через n лет (месяцев).

– процентная ставка.

Задачи на вклады решаются двумя способами: с помощью таблиц и с помощью формул. Рассмотрим задачу на вклад с ежегодным пополнением на определённую сумму.

 

I способ. Приведём пример таблицы накопления вклада. Таблицы удобны, если временной промежуток вклада невелик.

 

дата или № года (месяца)	% на сумму в конце года (месяца)	сумма с учётом %	сумма вклада	сумма в конце года (месяца)
0
1
2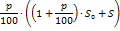
…	………	…………….		………….

 

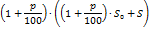
Из таблицы видно, что чем больше срок вклада, тем сложнее вычисления. Поэтому, при больших сроках удобнее пользоваться формулами.

 

II способ. Чтобы понять, откуда берётся формула, приведём её вывод. Воспользуемся таблицей выше. Рассмотрим сумму вклада в конце второго года (месяца).

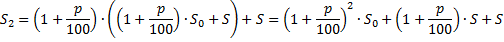
Аналогично,

И так далее,

В последнем выражении, в квадратных скобках стоит сумма п членов геометрической прогрессии, в которой . Воспользуемся формулой для .

Тогда общая сумма вклада через п лет (с учётом пополнения) будет:

Если же в n -ом году счёт будет закрыт, то последнего пополнения не будет! Тогда формула имеет вид:

  Если сумма ежегодного пополнения равна первоначальному взносу , то формула принимает более компактный вид:

В задачах на вклады без ежегодного пополнения ситуация немного проще.

 

дата или № года (месяца)	% на сумму в конце года (месяца)	сумма в конце года (месяца) с учётом %
0
1
2
…	………	…………….
через п лет

 

В виде формулы это выглядит так:

 

Приведём примеры.

 

1.1.1. Банк выплачивает 4 % годовых. Через сколько лет внесённая сумма удвоится?

Решение.

 – сумма вклада, , .

По окончании первого года, после начисления процентов, на счёте станет:

 

По окончании второго года, после начисления процентов, на счёте станет:

………………………………………………………………….

 

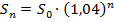
Так как , то

 

Отв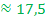ет:  лет

1.1.2. На какой срок необходимо вложить 5000 рублей при 30% годовых, чтобы сумма дохода составила 560 рублей?

Решение.

, , .

Так как сумма дохода равна , то срок вклада будем рассчитывать в днях, и т.к. нас интересует только доход, то . Эта формула означает следующее: на первоначальный взнос назначается годовой процент р, но т.к. срок вклада меньше года, то эту сумму делят на 365 дней и умножают на количество дней, в течении которых вклад находился в банке (п). Важно, что здесь не добавляется сам первоначальный взнос, т.е. формула отражает чистую прибыль.

 

Так как , то

                                                          

Ответ:  дней

 

1.1.3. На какой срок необходимо вложить 15 000 рублей при 9 % годовых, чтобы сумма дохода составила 2 000 рублей?

Решение.

, , .

Так как нас интересует только доход, то

 

Так как , то

                                                          

Ответ:  дней                                                                     

1.1.4. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом  и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на . Определите срок хранения вклада.

Решение.

 – сумма вклада;

месяцев – срок начисления 5% ставки;

месяцев – срок начисления 12% ставки;

месяцев – срок начисления % ставки;

месяцев – срок начисления 12,5% ставки.

 

При ставке 5% через месяц сумма вклада составила . Через два месяца сумма вклада составила . И так далее, через п месяцев сумма вклада составит .

При ставке 12% через месяц сумма вклада составит:

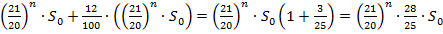. Через два месяца –

. И так далее, через т месяцев сумма вклада составит .

Аналогично, при ставке  через k месяцев сумма вклада будет .

Так же, при ставке 12,5% через l месяцев сумма вклада будет .

По условию задачи известно, что по истечении срока хранения первоначальная сумма увеличилась на , т.е. составила .

Составляем уравнение:

Значит, весь срок вклада составляет:  месяцев.

Ответ: 7 месяцев

1.1.5. Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладёт 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?

Решение. Сначала рассмотрим как происходит накопление денежных средств на счёте сына. Так как каждый год банк начисляет 20% на сумму, которая была в конце предыдущего года, то вся сумма будет составлять 120%. Затем прибавляем ежегодный взнос 1000 руб.

дата	сумма на счёте сына
01.09.2008
01.09.2009
01.09.2010
01.09.2011
……………	…………………………………………………………………………………
через n лет

 

Теперь рассмотрим сумму на счёте сына через n лет.

 В этой сумме  слагаемое (слагаемых со степенями п плюс первое слагаемое). Нетрудно заметить, что эта сумма представляет собой сумму геометрической прогрессии, у которой . Воспользуемся формулой суммы  членов геометрической прогрессии:  

Это сумма, которая будет на счёте сына через п лет.

дата	сумма на счёте дочери
01.09.2014
01.09.2015
01.09.2016
01.09.2017
……………	…………………………………………………………………………………
через n -6лет

Рассчитаем сумму на счёте дочери. Так как каждый год банк начисляет 44% на сумму, которая была в конце предыдущего года, то вся сумма будет составлять 144%. Затем прибавляем ежегодный взнос 2200 руб. и учитываем, что срок вклада дочери будет на 6 лет меньше, чем срок вклада сына, т.е.  лет.

 

Теперь рассмотрим сумму на счёте дочери через n - 6лет.

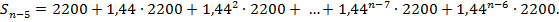 В этой сумме  слагаемых (слагаемых со степенями п - 6плюс первое слагаемое). Эта сумма представляет собой сумму геометрической прогрессии, у которой . Воспользуемся формулой суммы  членов геометрической прогрессии:

 

Это сумма, которая будет на счёте дочери через п - 6 лет.

В задаче поставлено условие, что суммы вкладов сына и дочери должны сравняться, поэтому приравниваем их.

Значит, суммы на счетах сына и дочери сравняются через 11 лет после открытия счёта сына. И это произойдёт в  году.

 

Ответ: в 2019 году.

 

1.1.6. Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение. Рассмотрим два способа решения данной задачи.

I способ. Составим сравнительную таблицу стоимости ценной бумаги после увеличения цены и банковского процента.

№ года	стоимость ценной бумаги в начале года	сумма увеличения стоимости ценной бумаги	общая стоимость ценной бумаги в конце года	банковский процент (8%)
1	8 000	1 000	9 000	720
2	9 000	1 000	10 000	800
3	10 000	1 000	11 000	880
4	11 000	1 000	12 000	960
5	12 000	1 000	13 000	1040

Из таблицы видно, что банковский процент превысит сумму увеличения стоимости ценной бумаги через 5 лет, значит, продавать бумаги надо в течение 6 лет.

 

II способ. Если ценная бумага будет находится у Алексея n лет, то через n лет он получит рублей. Если в начале го года Алексей продаст бумагу и положит деньги в банк, то по итогам года получит  Это следует делать, если . Найдем, каким должно быть число n.

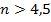
 – число целое, значит, . Так как Алексей положил деньги в банк в течении  года, то максимальную прибыль он получит, если положит деньги в банк в течении 6 года.

Ответ: в течении 6 года.

1.2.1. В январе 2000 года ставка по депозитам в банке «Возрождение» составила х% годовых, тогда как в январе 2001 года она была у% годовых, причём известно, что x + y = 30%. В январе 2000 года вкладчик открыл счёт в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счёта пятую часть этой суммы. Укажите значение х, при котором сумма на счёте вкладчика в январе 2002 года станет максимально возможной.

Решение. Пусть  – первоначальный вклад. При  годовых через год на счёте будет . После снятия со счёта , на нём осталось:

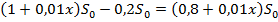. На эту сумму через год начислили  и на счёте стало . Так как , то . Тогда:

Мы получили функцию относительно переменной х:

Наибольшее значение эта квадратичная функция достигает в своей вершине, т.к. ветви её направлены вниз. Найдём абсциссу вершины параболы:

.

Итак, при  сумма на счёте вкладчика в январе 2002 года будет максимально возможной.

 

Ответ: 25%

 

1.2.2. Баба Валя, накопив часть своей пенсии, решила улучшить своё материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определённый процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить своё материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счёта в Спёрбанке, Баба Валя сняла половину образовавшейся суммы от её вклада, заявив: «Такой навар меня не устраивает!» И открыла счёт в том коммерческом банке, о котором говорила её соседка, не теряя надежды на значительное улучшение своего материального благосостояния. Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила её первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без навара! А каков в Спёрбанке процент годовых для пенсионеров?

Решение. Пусть  – первоначальные накопления;  - процентная ставка в Спёрбанке, тогда  - процентная ставка в коммерческом банке. Открыв счёт в Спёрбанке, через год на нём образуется сумма . В коммерческий банк была внесена сумма, равная половине этой, т.е. . Через год в коммерческом банке на счёте, после начисления процентов, будет . По условию задачи известно, что эта сумма на 65% больше, чем первоначальные накопления, т.е. составляет 165% от  и равна . Составляем уравнение:

  не удовлетворяет условию задачи, значит, в Спёрбанке процентная ставка равна 10%.

Ответ: 10%

1.2.3. Банк под определённый процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счёта. Банк увеличил процент годовых на 40 процентных пунктов (то есть увеличил ставку а% до (а + 40)%). К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

Решение. Обозначим первоначальный вклад через , а первоначальную процентную ставку через а %. Тогда через год, после начисления процентов на счёте станет  Четверть этой суммы сняли со счёта, тогда осталось:

. На эту оставшуюся сумму через год начислили проценты в размере . В итоге, к концу года на счёте накопилась сумма: . По условию задачи известно, что она превысила первоначальный вклад в 1,44 раз, т.е. стала равной . Составим уравнение:

 не удовлетворяет условию задачи. Значит, первоначальная процентная ставка составляла 20%. Поэтому новая процентная ставка равна: .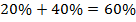

Ответ: 60%.

 

1.2.4. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 11 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».

Решение. Обозначим через  -  первоначальную сумму по обоим вкладам, а через  – процентную ставку вклада «Б» на третий год. Составим таблицу:

 

№ года	сумма в конце года с учётом процентов вклада «А»	сумма в конце года с учётом процентов вклада «Б»
0
1
2
3

 

Чтобы выполнялось условие задачи (вклад «Б» должен остаться более выгодным, чем вклад «А»), необходимо выполнение условия:

Т.к.  должно быть целым и наименьшим, то .

Ответ: 9%.

 

1.2.5. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Решение.

№ года	сумма в конце года с учётом процентов вклада «А»	сумма в конце года с учётом процентов вклада «Б»
0
1
2
3

 

Чтобы выполнялось условие задачи (вклад «Б» должен остаться более выгодным, чем вклад «А»), необходимо выполнение условия:

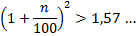
Так как , то .

Стоит заметить, что при . Это не удовлетворяет условию, как, впрочем, и все остальные значения, меньшие 26.

Итак, наименьшее целое .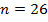

Ответ: 26%.

 

1.3.1. В начале года 5/6 некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е., к концу следующего — 749 у. е. Если первоначально 5/6 суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.

Решение. Обозначим  – общую первоначальную сумму, тогда в банк А вложили , а в банк Б вложили . Процентную ставку банка А обозначим через р, а процентную ставку банка Б – через q. Тогда через год на счёте в банке А стало , а на счёте в банке Б - . Через два года в банке А стало , а в банке Б - . Если бы изначально в банк А вложили бы , а в банк Б - , то через год в банке А было бы , а в банке Б - . Через два года в банке А было бы , а в банке Б - . Для наглядности сведём всё это в таблицу:

 

№ года	сумма в конце года банка А  при сумме вложения	сумма в конце года банка Б  при сумме вложения	общая сумма в конце года
1			670
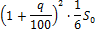
2			749
№ года	сумма в конце года банка А  при сумме вложения	сумма в конце года банка Б  при сумме вложения	общая сумма в конце года
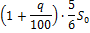
1			710
2			?

 

Итак, получаем систему уравнений:

Второе уравнение умножим на -5 и сложим с первым.

Теперь мы можем найти общую сумму в конце второго года во втором случае:

Ответ: 841 у.е.

1.3.2. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 2 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 15 млн рублей.

Решение.

№ года	сумма на счёте
0
1
2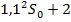
3
4

Итоговая сумма должна быть меньше 15 млн. рублей, поэтому:

Так как первоначальный вклад является целым числом и должен быть наибольшим, то 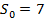 млн. рублей.

 

Ответ: 7 млн. рублей.

1.3.3. По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 125 миллионов, а за четыре года станут больше 200 миллионов рублей.

Решение.

№ года	сумма с учётом процентов и вложений
0	млн
1
2
3
4

По условию задачи через два года сумма должна быть больше 125 млн. рублей, а через 4 года – больше 200 млн. рублей, поэтому:

Так как  – наименьшее целое, то  млн. рублей.

Ответ: 57 млн. рублей.

 

1.4.1. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырёх лет хранения после начисления процентов вкладчик дополнительно вносил на счёт одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял ко вкладу?

Решение. В данной задаче рассматривается вклад с пополнением. Обозначим через  тыс. рублей ежегодную сумму пополнения. Тогда сведём данные в таблицу:

№ года	сумма на счёте
0
1
2
3
4
5

 

Итак, в конце пятого года, после начисления процентов на счёте оказалась сумма:

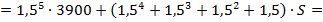
По условию задачи известно, что в конце пятого года размер вклада увеличился по сравнению с первоначальным на 725%, т.е. стал составлять 825% от первоначального.. Составляем уравнение:

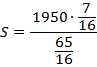
Значит, ежегодное пополнение составляло 210 тыс. рублей.

Ответ: 210 000 рублей

 

1.4.2. По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.

Решение. Составим таблицу:

№ года	сумма с учётом процентов и вложений
0	10 млн
1
2
3
4

 

По условию задачи за два года вложения должны как минимум удвоиться, поэтому,

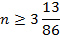
Значит, наименьшее целое