Примеры решения задач по гидростатике

ЗАДАНИЯ

К выполнению расчетно – графической работы

По дисциплине «Гидравлика»

Тема: гидростатика

Северодвинск

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Гидравлика, или техническая механика жидкостей— это наука о законах равновесия и движения жидкостей, о способах применения этих законов к решению практических задач;

Жидкостью называют вещество, находящееся в таком агрегатном состоянии, которое сочетает в себе черты твердого состояния (весьма малая сжимаемость) и газообразного (текучесть). Законы равновесия и движения капельных жид­костей в известных пределах можно применять и к газам.

На жидкость могут действовать силы, распределенные по ее массе (объему), называемые массовыми, и по поверхности, называемые поверхностными. К первым относятся силы тя­жести и инерции, ко вторым — силы давления и трения.

Давлением называется отношение силы, нормальной к по­верхности, к площади. При равномерном распределении

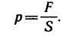
Касательным напряжением называется отношение силы трения, касательной к поверхности, к площади:

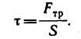
Если давление р отсчитывают от абсолютного нуля, то его называют абсолютным (р_абс), а если от условного нуля (т. е. сравнивают с атмосферным давлением р_а, то избыточным (р_изб):

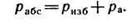
Если Р_абс< Р_а, то имеется вакуум, величина которого:

Р_вак = Р_а - Р_абс

Основной физической характеристикой жидкости является плотность ρ (кг/м³), определяемая для однородной жидкости отношением ее массы m к объему V:

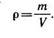
Плотность пресной воды при температуре Т = 4°С ρ = = 1000 кг/м³. В гидравлике часто пользуются также понятием удельного веса γ (Н/м³), т.е весом G единицы объема жидкости:

Плотность и удельный вес связаны между собой соотношением:

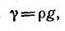
где g — ускорение свободного падения.

Для пресной воды γ_вод= 9810 Н/м³

Важнейшие физические параметры жидкостей, которые используются в гидравлических расчетах,— сжимаемость, температурное расширение, вязкость и испаряемость.

Сжимаемость жидкостей характеризуется модулем объемной упругости К, входящим в обобщенный закон Гука:

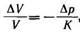
где ΔV — приращение (в данном случае уменьшение) объема жидкости V, обусловленное увеличением давления на Δр. Например, для воды К_вод ≈2^.10³ МПа.

Температурное расширение определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С:

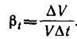
Вязкость — это способность жидкости сопротивляться сдвигу. Различают динамическую (μ) и кинематическую (ν) вязкости. Первая входит в закон жидкостного трения Ньютона, выражающий касательное напряжение τ через поперечный градиент скорости dv/dt:

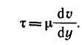
Кинематическая вязкость связана с динамической соотношением

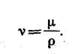
Единицей кинематической вязкости является м²/с.

Испаряемость жидкостей характеризуется давлением насыщенных паров в функции температуры.

Давлением насыщенных паров можно считать то абсолютное давление, при котором жидкость закипает при данной температуре. Следовательно, минимальное абсолютное давление, при котором вещество находится в жидком состоянии, равно давлению насыщенных паров р _н.п.

 

Основные параметры некоторых жидкостей, их единицы в СИ и внесистемные единицы, временно допускаемые к применению, приведены в Приложениях 1...3.

ГИДРОСТАТИКА

 

Давление в неподвижной жидкости называется гидростатическим и обладает следующими двумя свойствами:

- на внешней поверхности жидкости оно всегда направлено во нормали внутрь объема жидкости;

- в любой точке внутри жидкости оно по всем направлениям одинаково, т. е. не зависит от угла наклона площадки, по которой действует.

Уравнение, выражающее гидростатическое давление р в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на нее действует лишь одна сила тяжести, называется основным уравнением гидростатики:

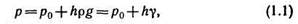
где p₀ — давление на какой-либо поверхности уровня жидкости, например на свободной поверхности; h — глубина расположения рассматриваемой точки, отсчитанная от поверхности с давлением р₀.

В тех случаях, когда рассматриваемая точка расположена выше поверхности с давлением р₀, второй член в формуле (1.1) отрицателен.

Другая форма записи того же уравнения (1.1) имеет вид

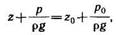^(1.2)

где z и z₀ — вертикальные координаты произвольной точки и свободной поверхности, отсчитываемые от горизонтальной плоскости вверх; p/(pg) — пьезометрическая высота.

Гидростатическое давление может быть условно выражено высотой столба жидкости p/ρg.

В гидротехнической практике внешнее давление часто равноатмосферному: P₀=Р_ат

Величина давления P_ат = 1 кГ/см² = 9,81^.10⁴ н/м^г называется технической атмосферой.

Давление, равное одной технической атмосфере, эквивалентно давлению столба воды высотой 10 метров, т. е.

Гидростатическое давление, определяемое по уравнению (1.1), именуется полным или абсолютным давлением. В дальнейшем будем обозначать это давление р_абс или p’. Обычно в гидротехнических расчетах интересуются не полным давлением, а разницей между полным давлением в атмосферным, т. е. так называемым манометрическим давлением

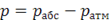
В дальнейшем изложении сохраним обозначение р за манометрическим давлением.

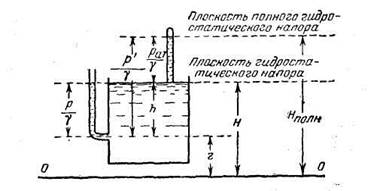
Рисунок 1.1

Сумма членов 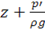дает величину полного гидростатического напора

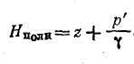
Сумма 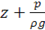—- выражает гидростатический напор Н без учета атмосферного давления p_ат/ρg, т. е.

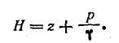
На рис. 1.1 плоскость полного гидростатического напора и плоскость гидростатического напора показаны для случая, когда свободная поверхность находится под атмосферным давлением р₀=p_ат.

Графическое изображение величины и направления гидростатического давления, действующего на любую точку поверхности, носит название эпюры гидростатического давления. Для построения эпюры нужно отложить величину гидростатического давления для рассматриваемой точки нормально к поверхности, яа которую оно действует. Так, например, эпюра манометрического давления на плоский наклонный щит АВ (рис. 1.2,а) будет представлять треугольник ABC, а эпюра полного гидростатического давления — трапецию A'B'C'D' (рис. 1.2,б).

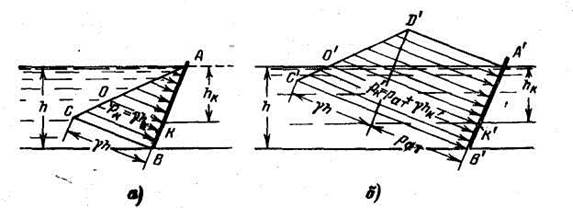
Рисунок 1.2

Каждый отрезок эпюры на рис. 1.2,а (например О К) будет изображать манометрическое давление в точке К, т. е. p_K = ρgh_K, а на рис. 1.2,б — полное гидростатическое давление

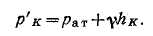
Сила давления жидкости на плоскую стенку равна произведению гидростатического давления ρ_с в центре тяжести площади стенки на площадь стенки S, т. е.

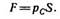
Центр давления (точка приложения силы F) расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки.

Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно

где J₀ — момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью: у_с — координата центра тяжести площади.

Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной F_Г и вертикальной F_B составляющих:

Горизонтальная составляющая F_Г равна силе давления жидкости на вертикальную проекцию данной стенки:

Вертикальная составляющая F_B равна весу жидкости в объеме V, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проекцирующей поверхностью, проведенной по контуру стенки.

Если избыточное давление р₀ на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту) p₀/(ρg)

Плавание тел и их остойчивость. Условие плавания тела выражается равенством

G=P (1.6)

где G — вес тела;

Р — результирующая сила давления жидкости на погруженное в нее тело — архимедова сила.

Сила Р может быть найдена по формуле

P=ρgW (1.7)

где ρg — удельный вес жидкости;

W — объем жидкости, вытесненной телом, или водоизмещение.

Сила Р направлена вверх и проходит через центр тяжести водоизмещения.

Осадкой тела у называется глубина погружения наинизшей точки смоченной поверхности (рис. 1.3,а). Под осью плавания понимают линию, проходящую через центр тяжести С и центр водоизмещения D, соответствующий/ нормальному положению тела в состоянии равновесия (рис. 1.3, а )-

Ватерлинией называется линия пересечения поверхности плавающего тела со свободной поверхностью жидкости (рис. 1.3,б). Плоскостью плавания ABEF называется плоскость, полученная от пересечения тела свободной поверхностью жидкости, или, иначе плоскость, ограниченная ватерлинией.

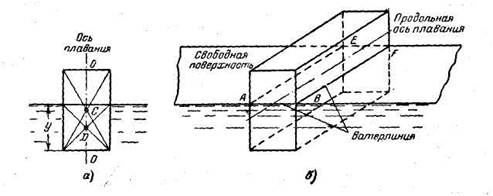
Рисунок 1.3

Кроме выполнения условий плавания (1.5) тело (судно, баржа и т.д.) должно удовлетворять условиям остойчивости. Плавающее тело будет остойчивым в том случае, если при крене сила веса G и архимедова сила Р создают момент, стремящийся уничтожить крен и вернуть тело в исходное положение.

Рисунок 1.4

При надводном плавании тела (рис. 1.4) центр водоизмещения при малых углах крена (α<15°) перемещается по некоторой дуге, проведенной из точки пересечения линии действия силы Р с осью плавания. Эта точка называется метацентром (на рис. 1.4 точка М). Будем в дальнейшем рассматривать условия остойчивости лишь при надводном плавании тела при малых углах крена.

Если центр тяжести тела С лежит ниже центра водоизмещения, то плавание будет безусловно остойчивым (рис. 1.4,а).

Если центр тяжести тела С лежит выше центра водоизмещения D, то плавание будет остойчивым только при выполнении следующего условия (рис. 1-9,б):

ρ>δ (1.7)

где ρ — метацентрический радиус, т. е. расстояние между центром водоизмещения и метацентром

δ — расстояние между центром тяжести тела С и центром во­доизмещения D. Метацентрический радиус ρ находится по формуле:

^(1.8)

где J₀ — момент инерции плоскости плавания или площади, ограниченной ватерлинией, относительно продольной оси (рис. 1-8,6);

W — водоизмещение.

Если центр тяжести тела С расположен выше центра водоизмещения и метацентра, то тело неостойчиво; возникающая пара сил G и Р стремится увеличить крен (рис. 1.4, в).

 

УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

При решении задач по гидростатике прежде всего нужно хорошо усвоить и не смешивать такие понятия, как давление р и сила F.

При решении задач на определение давления в той или иной точке неподвижной жидкости следует пользоваться основным уравнением гидростатики (1.1). Применяя это уравнение, нужно иметь в виду, что второй член в правой части этого уравнения может быть как положительным, так и отрицательным. Очевидно, что при увеличении глубины давление возрастает, а при подъеме — уменьшается.

Необходимо твердо различать давления абсолютное, избыточное и вакуум и обязательно знать связь между давлением, удельным весом и высотой, соответствующей этому давлению (пьезометрической высотой).

При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, т. е. равенство нулю суммы всех сил, действующих на поршень (систему поршней).

Решение задач следует проводить в международной системе единиц измерения СИ.

Решение задачи должно сопровождаться необходимыми пояснениями, рисунками (принеобходимости), перечислением исходных величин (графа «дано»), переводом единиц в систему СИ.

 

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ГИДРОСТАТИКЕ

Задача 1. Определить полное гидростатическое давление на дно сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде h = 0,60 м.

Решение:

В данном случае имеем р₀=р_ат и потому применим формулу (1.1) в виде

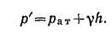
р'=9,81.10⁴ +9810^.0,6 = 103986 Па

Ответ р’=103986 Па

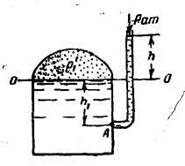Задача 2. Определить высоту столба воды в пьезометре над уровнем жидкости в закрытом сосуде. Вода в сосуде находитcя под абсолютным давлением p'₁ = 1,06 ат (рисунок к задаче 2).

Решение.

Составим условия равновесия для общей точки А (см. рисунок ). Давление в точке А слева:

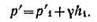
Давление справа:

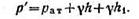
Приравнивая правые части уравнений, и сокращая на γg получаем:

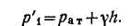
Указанное уравнение можно также получить, составив условие равновесия для точек, расположенных в любой горизонтальной плоскости, например в плоскости ОО (см. рисунок). Примем за начало шкалы отсчета пьезометра плоскость ОО и из полученного уравнения найдем высоту столба воды в пьезометре h.

Высота h равна:

= 0,6 метра

Пьезометр измеряет величину манометрического давления, выраженного высотой столба жидкости.

Ответ: h = 0,6 метра

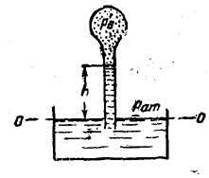Задача 3. Определить высоту, на которую поднимается вода в вакуумметре, если абсолютное давление воздуха внутри баллона р’_в=0,95 ат (рис. 1-11). Сформулировать, какое давление измеряет вакуумметр.

Решение:

Составим условие равновесия относительно горизонтальной плоскости О-О:

гидростатическое давление, действующее изнутри:

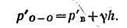
Гидростатическое давление в плоскости О — О, действующее с внешней стороны,

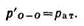
Так как система находится в равновесии, то

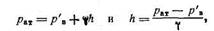
т. е. вакуумметр измеряет недостаток давления до атмосферного или вакуум, выраженный высотой столба жидкости.

Высота, на которую поднимается жидкость, при γ=9810 Н/м³

Ответ: h = 0,5 метра

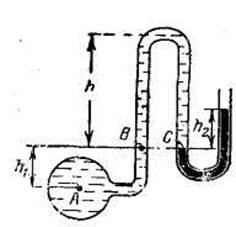Задача 4. Определить манометрическое давление в точке А трубопровода, если высота столба ртути по пьезометру h₂=25 см. Центр трубопровода расположен на h₁ =40 см ниже линии раздела между водой и ртутью (рисунок к задаче).

Решение: Находим давление в точке В: р'_В=р'_А -γ h₁, так как точка В расположена выше точки А на величину h₁. В точке С давление будет такое же, как в точке В, так как давление столба воды h взаимно уравновешивается, т. е.

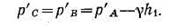
Определим давление в точке С справа с учетом атмосферного давления, т. е.

 

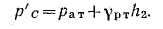
Приравнивая оба уравнения, получаем:

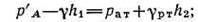
отсюда манометрическое давление:

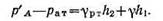
Подставляя числовые значения, получаем:

р'_А-р_атм =37278 Па

Ответ: р'_А-р_атм =37278 Па

ЗАДАЧИ

Задача 1.1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 ⁰С. Модуль объемной упругости бензина принять равным K=1300 МПа, коэффициент температурного расширения β = 8^.10^-4 1/град.

Задача 1.2. Определить избыточное давление на дне океана, глубина которого h=10 км, приняв плотность морской воды ρ=1030 кг/м³ и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости K = 2^.10³ МПа.

Задача 1.3. Найти закон изменения давления р атмосферного воздуха по высоте z, считая зависимость его плотности от давления изотермической. В действительности до высоты z=11 км температура воздуха падает по линейному закону, т. е. T=T₀-β_z, где β = 6,5 град/км. Определить зависимость p = f(z) с учетом действительного изменения температуры воздуха с высотой.

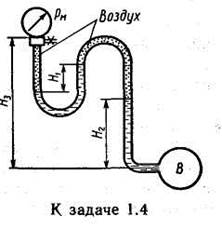
Задача 1.4. Определить избыточное давление воды в трубе В, если показание манометра р_м = 0,025 МПа. Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем Н₁ = 0,5 м; Н₂=3 м.

Как изменится показание манометра, если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран К)? Высота Н₃ = 5 м.

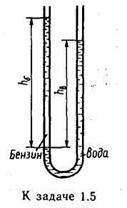Задача 1.5. В U-образную трубку налиты вода и бензин. Определить плотность бензина, если h_б = 500 мм; h_в = = 350 мм. Капиллярный эффект не учитывать.

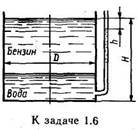Задача 1.6. В цилиндрический бак диаметром D = 2 м до уровня Н=1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить веснаходящегося в баке бензина, если ρ_б = 700 кг/м³.

 

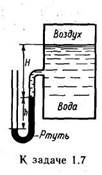
Задача 1.7. Определить абсолютное давление воздуха всосуде, если показание ртутного прибора h = 368 мм, высота H=1 м. Плотность ртути ρ= 13600 кг/м³. Атмосферное давление 736 мм рт. ст.

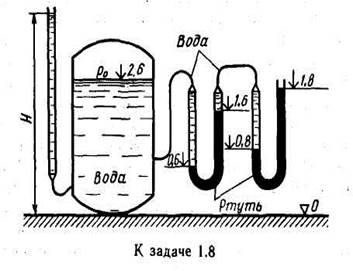Задача 1.8. Определить избыточное давление p₀воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты Н должен быть пьезометр для измерения того же давления p₀ Плотность ртути ρ = 13600 кг/м³.

 

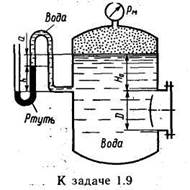Задача 1.9. Определить силу давления жидкости (воды) на крышку люка диаметром D=l м в следующих двух случаях:

1) показание манометра р_м = 0,08 МПа; H₀=1,5 м;

2) показание ртутного вакуумметра h = 73,5 мм при а= 1м; ρ_рт= 13600 кг/м³; Н₀=1,5 м.

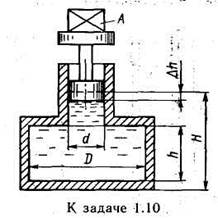Задача 1.10. Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние Δh = 5 мм. Начальная высота положения поршня (без груза) H =1,5 м, диаметры поршня d = 80 мм н резервуара D = 300 мм, высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким.

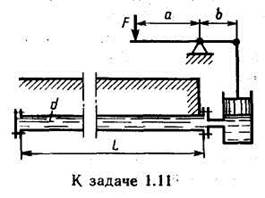Задача 1.11. Для опрессовки водой подземного трубопровода (проверки герметичности) применяется ручной поршневой насос. Определить объем воды (модуль упругости К = 2000 МПа), который нужно накачать в трубопровод для повышения избыточного давления в нем от 0 до 1,0 МПа. Считать трубопровод абсолютно жестким. Размеры трубопровода: длина L = 500 м, диаметр d=100 мм. Чему равно усилие на рукоятке насоса в последний момент опрессовки, если диаметр поршня насоса d_n = 40 мм, а соотношение плеч рычажного механизма а/в = 5?

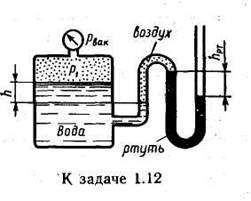Задача 1.12. Определить абсолютное давление воздуха в баке р₁, еcли при атмосферном давлении, соответствующем h_а = 760 мм рт. ст., показание ртутного вакуумметра h_рт = = 0,2 м, высота h =1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути ρ=13600 кг/м³.

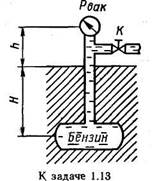
Задача 1.13. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине Н=5 м, если показание вакуумметра, установленного на высоте h=1,7 м, равно р_вак = 0,02 МПа. Атмосферное давление соответствует р_а = 740 мм рт. ст. Плотность бензина ρ_б = 700 кг/м³.

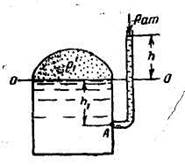Задача 1.14. Определить давление р’₁, если показание пьезометра h =0,4 м. Чему равно манометрическое давление?

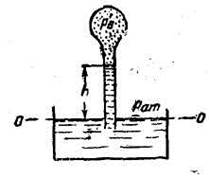
Задача 1.15. Определить вакуум р_вак и абсолютное давление внутри баллона р'_в (рис. 1-11), если показание вакуумметра h =0,7 м вод. ст.

 

 

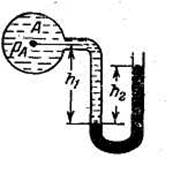Задача 1.16. Подсчитать манометрическое и абсолютное давление в баллоне А (рисунок) в двух случаях:

1) в баллоне и в левой трубке — вода, а в правой трубке — ртуть (ρ=13600 кг/м³ );

2) в баллоне и левой трубке — воздух, а в правой трубке - вода.

Определить, какой процент составляет давление столба воздуха в трубке от вычисленного во втором случае манометрического давления?

При решении задачи принять h₁ = 70 см,h ₂= = 50 см.

Задача 1.17. Чему будет равна высота ртутного столба h₂ (рис. к задаче 1.16), если манометрическое давление нефти в баллоне А p_а = 0,5 ат, а высота столба нефти (ρ=800 кг/м³) h ₁=55 см?

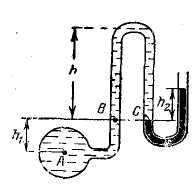Задача 1.18. Определить высоту столба ртути h₂, (рисунок), если расположение центра трубопровода А повысится по сравнению с указанным на рисунке и станет на h₁ = 40 см выше линии раздела между водой и ртутью. Манометрическое давление в трубе принять 37 278 Па.

 

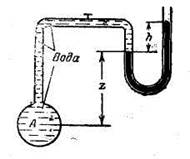Задача 1.19. Определить, на какой высоте z установится уровень ртути в пьезометре, если при манометрическом давлении в трубе Р_А =39240 Па и показании h=24 см система находится в равновесии (см. рисунок).

 

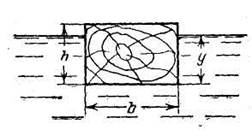Задача 1.20. Определить удельный вес бруса, имеющего сле­дующие размеры: ширину b=30 см, высоту h=20 см и длину l = 100 см, если его осадка y=16 см

Задача 1.21. Кусок гранита весит в воздухе 14,72 Н и 10,01 Н в жидкости, имеющей относительный удельный вес 0,8. Определить объем куска гранита, его плотность и удельный вес.

Задача 1.22 Деревянный брус размером 5,0^х0,30 м и высотой 0,30м спущен в воду. На какую глубину он погрузится, если от­носительный вес бруса 0,7? Определить, сколько человек могут встать на брус, чтобы верхняя поверхность бруса оказалась бы заподлицо со свободной поверхностью воды, считая, что каждый человек в среднем имеет массу 67,5 кг.

Задача 1.23 Прямоугольная металлическая баржа длиной 60 м, шириной 8 м, высотой 3,5 м, загруженная песком, весит 14126 кН. Определить осадку баржи. Какой объем песка V_п нужно выгрузить, чтобы глубина погружения баржи была 1,2 м, если относительный удельный вес влажного песка равен 2,0?

Задача 1.24. Объемное водоизмещение подводной лодки 600 м³. С целью погружения лодки отсеки были заполнены морской водой в количестве 80 м³. Относительный удельный вес морской воды 1,025. Определить: какая часть объема лодки (в процентах) будет погружена в воду, если из подводной лодки удалить всю воду и она всплывет; чему равен вес подводной лодки без воды?

Поделиться:

Воспользуйтесь поиском по сайту: