 |
Оценка прочности по касательным напряжениям.
|
|
|
|
ЗАДАЧА 5
Для консольной балки из чугуна (рис. 1), имеющей поперечное сечение согласно рис. 2 (из РГР 2) требуется:
1. Построить эпюры поперечных сил и изгибающих моментов.
2. Определить геометрические характеристики поперечного сечения: положение центра тяжести сечения, направление главных центральных осей, главные центральные моменты инерции.
3. Проверить прочность балки.
4. Построить эпюру касательных напряжений в наиболее опасном сечении и дать оценку прочности по касательным напряжениям.
5. Построить эпюру прогибов поперечных сечений балки методом начальных параметров.
6. Проверить жесткость балки по прогибам, если допускаемый прогиб: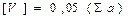 
.
Исходные данные: a = 1 м; F1 = 20 кH, F3 = 10 кH; q2 = 30 кН/м; m2 = 10 кН.м; m3 = 30 кН.м; Е = 1,4.105 МПа; [ sp ] = 45 МПа; [ scж ] = 47 МПа; [ t ] = 30 МПа; с = 0,425 R; d = 6 см.
Решение.
1. Введем и обозначим общую систему координат XYZ с началом в точке А, совпадающей с жестким защемлением (рис. 3а). На схеме нагрузок изображаем опорные реакции RA и mA.
2. Составляем уравнения равновесия балки и определяем опорные реакции.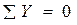 
; 
.
; 
Проверка: 
;
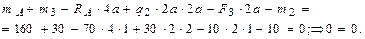
3. Разбиваем балку на четыре участка и строим эпюры Q и М (рис. 3б; 3 в):
Участок I: 
Q=RA=70 кН; M=-mA+RA.Z;
При Z=0; Q=70 кН; M=-160 кН.м.
При Z=а; Q=70 кН; M=-90 кН.м.
Участок II: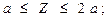 
Q=RA- q2. (Z-a);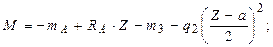 
При Z=a: Q=70 кН; M=- 120 кH.м ;
При Z=2a: Q=40 кН; M=- 65 кH. м.
Участок III: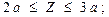 
.
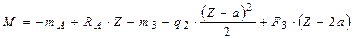При Z=2a: Q=50 кН; М=- 65 кН. м.
При Z=3a: Q=20 кН; М=- 30 кН. м.
Участок IV: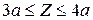 
Q=RA-q2. 2a +F3 ;
M==- mA+RA. Z - m3 - q2. 2a(Z - 2a)+F3 . (Z - 2a)+m2.
При Z=3a: Q=20 кН; M=- 20 кН. м;
При Z=4a: Q=20 кН; M=0.
4. Определение геометрических характеристик поперечного сечения балки (Поперечное сечение взять из рис. РГР-2) 
Поскольку фигура симметричная, то главная ось Yc совпадает с осью симметрии фигуры У. Определяем положение второй главной оси Хс. Проводим вспомагательную ось Х по нижнему основанию фигуры и определяем положение центра тяжести поперечного сечения, предварительно разбив его на вспомогательные фигуры:
|
|
|
I прямоугольник со сторонами 3d´2d;
II квадрат со сторонами d´ d;
III полукруг с радиусом R= d.
Проведем ось ХС.
Вычисляем моменты инерции вспомогательных фигур относительно собственных центральных осей:
.
4.
Вычисляем главный центральный момент инерции:
5. Проверим прочность балки на изгиб по условию 
.
По эпюре изгибающих моментов определяем положение опасного сечения. Им является сечение А (заделка) с максимальным изгибающим моментом Мmax=160 кН.м. Вычисляем наибольшие растягивающие и сжимающие напряжения в поперечном сечении балки:
Условия прочности не соблюдаются:
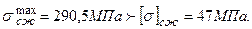
Кратность перегруза составляет:
Производим перерасчет размеров поперечного сечения по условию прочности для растянутой зоны, т.к. перегруз больше по растягивающим напряжениям:
Из последних двух выражений приравняв их получим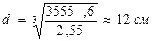 
Т.о. получили, что все размеры поперечного сечения балки необходимо увеличить в два раза. Тогда определим геометрические характеристики нового сечения:
.
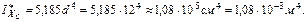
В дальнейшем в обозначениях характеристик нового сечения звездочку (*) указывать не будем.
Определим наибольшие нормальные напряжения в опасных точках сечения:
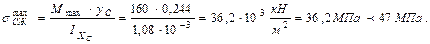
Оценка прочности по касательным напряжениям.
Согласно эпюре Q максимальное значение поперечной силы наблюдается на участке I: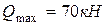 
.
Для определения сечения, где действуют наибольшие касательные напряжения, построим эпюру касательных напряжений, используя формулу Журавского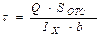 
.
Точка D: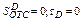 
Cечение 1-1:
где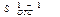 
- cтатический момент фигуры расположенной выше сечения 1-1 относительно оси ХС (полукруг).
Сечения 2-2: 
где S1122- cтатический момент прямоугольника, отсекаемого сечениями 1-1 и 2-2 относительно оси ХС;
|
|
|
у1122- кордината центра тяжести прямоугольника 1-1-2-2 относительно оси ХС.
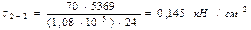
Сечение 3-3: 
Cечение 4-4:
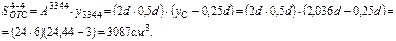
Сечение 41-41:
Сечение 5-5:
Сечение 51-51:
.
По найденным значениям строим эпюру t (рис. 4).
Проверка: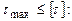 
.
Проверка выполняется.
|
|
|
