 |
Формула размещений без повторений
|
|
|
|
Основные правила и формулы комбинаторики
Основные правила комбинаторики
Во многих случаях для того, чтобы подсчитать число всех возможных исходов опыта, нужно перебрать огромное количество вариантов. Чтобы формализовать эту задачу и правильно подсчитать общее число опытов используют комбинаторные формулы.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из конечного множества данных объектов.
При выводе комбинаторных формул руководствуются двумя правилами.
1) Правило суммы.
Если объект 
можно выбрать 
способами, а объект B – k способами, то объект либо , либо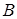 
можно выбрать 
способами.
Пример. В корзине лежат белые, синие и красные шары. Если синих шаров 5, а красных – 7, то цветной шар (либо красный, либо синий) можно выбрать 7 + 5 = 12 способами.
2) Правило произведения.
Если объект можно выбрать способами, а объект – 
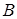способами, то пару 
можно выбрать 
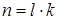способами.
Пример. Подарочный набор состоит из флакона духов и помады. Имеются духи трех видов, помада — пяти тонов. Сколько различных наборов можно составить? Так как каждый из трех видов духов можно дополнить помадой 5 цветов, то всего получится 
вариантов подарочных наборов.
Теперь перейдем к рассмотрению и подсчету числа различных комбинаций.
Формула размещений без повторений
Размещения без повторений получаются по следующей схеме. Имеется n различных предметов. Из них выбирают 
предметов так, что меняется и состав выбранных предметов и порядок их расположения относительно друг друга. Представить такую ситуацию можно следующим образом. Рисуем ряд из клеток
|
|
|
| 1 | 2 | 3 | .......... | m |
Берем произвольный предмет из 
имеющихся и помещаем в первую клетку (это можно сделать способами), затем берем любой из оставшихся 
предметов и помещаем во вторую клетку ( способами). Значит, по правилу произведения, пару — первую и вторую клетку — можно заполнить () способами. Рассуждая аналогично, найдем, что число способов разместить предметов из в клетках — число размещений из по обозначаемое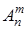 
, равно
.
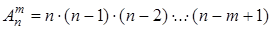Используя обозначения 
и 
формулу для размещений можно переписать по-другому:
.
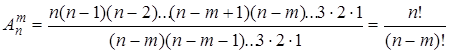Пример. Коротышки, проживающие в Цветочном городе, решили провести выборы городского начальства: мэра, вице-мэра, казначея, полицмейстера. Договорились, что каждый коротышка может претендовать на любой пост, но может быть выбран только на один пост. Сколькими способами можно выбрать городское начальство, если в городе 100 коротышек?
В этой задаче = 100, = 4. Первый пост – мэра, может занять любой из 100 жителей, вице-мэром может стать любой из оставшихся 99, казначеем – один из 98, и, наконец, полицмейстером любой из 97. Всего способов выбрать начальство:
.
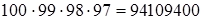2.3. Формула перестановок
Перестановки получаются, если различных предметов располагать в различном порядке (например, книги на полке). Число перестановок из предметов, обозначаемое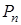 
, можно найти, если в предыдущей схеме размещений считать, что 
. Тогда
Пример. Из цифр 1, 2, 3, 5 составляются всевозможные четырехзначные числа так, чтобы цифры не повторялись. Сколько чисел можно составить?
Так как цифры не могут повторяться, значит, различные числа могут различаться только расположением цифр, т.е. число перестановок из различных цифр: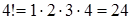 
.
2.4. Формула сочетаний без повторений
Такая комбинация получается, если при выборке предметов из важен только состав выборки, а не порядок расположения элементов выборки. Например, если коротышки из Цветочного города будут выбирать не начальство, где важно, кто какой пост занимает, а делегацию из четырех коротышек для поездки в Солнечный город, в которой важен только состав.
|
|
|
Число сочетаний из объектов по обозначается 
. Найдем его, используя следующее соображение. Чтобы получить все возможные размещения нужно взять выборку из предметов по определенного состава и произвести в ней все возможные перестановки. Затем взять другой состав и снова переставить и т.д.
Тогда число размещений (по правилу произведения) будет равно
,
откуда для числа сочетаний получим:
.
Число сочетаний используется в формуле бинома (двучлена) Ньютона
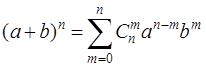
и поэтому еще называется биномиальным коэффициентом.
Пример. Подсчитаем, сколько различных делегаций из четырех коротышек можно составить для поездки в Солнечный город. Здесь = 100, = 4, поэтому количество делегаций равно
.
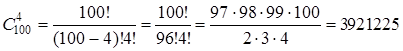2.5. Формула размещений с повторениями
Размещения с повторениями можно получить следующим образом. Ячейку из клеток заполняем, используя различных типов (классов) предметов. Первую клетку можно заполнить способами, вторую - также способами (поскольку каждый предмет не в единственном числе, а может повторяться сколько угодно раз), третья клетка заполняется также способами и т.д. Тогда число размещений с повторениями, обозначаемое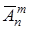 
, равно
.
Пример. Подсчитаем число четырехзначных автомобильных номеров. Номер составляется из 10 видов цифр. Т.к. в номерах и на первом месте может стоять 0 (в отличие от обычных чисел), то первую цифру можно выбрать 10 способами, вторую – 10 и т.д. и всего номеров будет 
. (Правда, по неизвестной причине номер 0000 не используется).
2.6. Формула сочетаний с повторениями
Сочетания с повторениями образуются так. Имеются объекты различных типов (классов). Выбираем предметов, взяв 
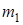предметов первого типа, 
предметов второго типа и т.д. так, что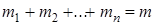 
. Значения 
могут меняться (от 0 до ), порождая различные наборы. Чтобы подсчитать их число, представим отдельный такой набор в виде ячейки из 
клеток, в которой единицы показывают клетки, занятые объектами различных классов ( штук), а нули — границы между классами или отсутствующие классы ( штука):
|
|
|
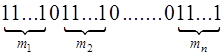
Различные комбинации будут различаться только положением нулей в ячейке. Т.е. изменение состава выборки связано с различным выбором мест из мест для нулей. Это число равно числу сочетаний из по . Таким образом, число сочетаний с повторениями из по , обозначаемое 
равно
.
Пример. Почетный караул составляется из военнослужащих 5 родов войск и состоит из 12 человек. Сколькими различными способами можно составить команду для почетного караула? В данном случае = 12, = 5 и число возможных способов равно
.
2.7. Формула перестановок с повторениями
Перестановки с повторениями получаются в следующем случае. Имеется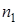 
объектов первого вида, 
— объектов второго вида и т.д., причем, 
. Если эти объекты выстроим в ряд и будем переставлять, то перестановки, в которых элементы одного вида будем менять местами, не будут отличаться друг от друга. С учетом этого, число перестановок с повторениями:
.
Пример. Сколько различных комбинаций букв можно получить при перестановке букв в слове “математика”? Всего 10 букв: 2 буквы м, 3 буквы а, 2 буквы т, по одной е, и, к. Значит, число комбинаций равно
.
|
|
|
