Таким образом, энергия плоской волны состоит из равных долей энергии электрического и магнитного полей.

 

Поляризация радиоволн

 

Электромагнитные волны бывают поляризованными и неполяризованными. Волны называются поляризованными, если направления векторов и в пространстве могут быть определены в любой момент времени. Если же направления и изменяются во времени случайным образом, то волна называется неполяризованной. Для радиосвязи естественно использовать поляризованные волны, что даёт возможность эффективного приёма радиосигналов при известном законе изменения и в пространстве.

Виды поляризации различаются законом изменения в пространстве плоскости поляризации, т.е. плоскости, проходящей через вектора и 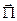. Если плоскость поляризации остаётся неподвижной по мере распространения волны, то такая поляризация называется линейной. Примеры линейно поляризованных волн представлены на рис.1.2.

 

 

Вектор может быть расположен под углом к плоскости х или у. В этом случае он образован суммой двух векторов:

 

 

Если векторы и колеблются синфазно во времени, то поляризация остаётся линейной. Если же антенной (при z=0) возбуждаются колебания и , сдвинутые по фазе на ц=±90є, например

 

 

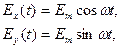
то суммарный вектор Е вращается. Конец вектора (а следовательно, и ) описывает окружность с центром в начале координат. Такая поляризация называется круговой.

В случае неравенства амплитуд колебаний и поляризация становится эллиптической - рис.1.3. Круговую и эллиптическую поляризацию называют также вращающейся с левым или с правым вращением.

 

 

При распространении волны с вращающейся поляризацией концы векторов и описывают в пространстве винтовые линии.

 

1.7 Представление монохроматических волн в виде комплексных. амплитуд

 

В случае монохроматических волн колебания в некоторой точке пространства имеют вид

 

(1.12)

 

Функцию такого вида можно рассматривать как действительную часть показательной функции , где i -мнимая единица. Действительно, в cоответствии с формулой Эйлера

 

 

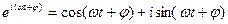
Поскольку линейные операции – сложение, вычитание, дифференцирование и интегрирование над комплексными числами осуществляются раздельно для действительных и мнимых частей, можно заменить функцию функцией . При этом, совершая линейные операции над функцией, нужно помнить, что интересует преобразования лишь линейных частей.

Таким образом, вместо колебаний вида (1.12) будем пользоваться формой записи

 

 

где

 

комплексная амплитуда, т.е. величина, несущая информацию об амплитуде Em и начальной фазе ц гармонических колебаний.

Такая замена выгодна тем, что при линейных операциях над гармоническими функциями сохраняется множитель . Это очевидно в случае сложения и вычитания. Аналогично при дифференцировании и интегрировании функции

 

 

,

 

 

В результате множитель при преобразованиях гармонических функций можно отбросить и производить операции не над мгновенными значениями функций, а над комплексными амплитудами, что существенно упрощает анализ. При этом нужно помнить, что комплексная амплитуда производной функции равна комплексной амплитуде исходной функции, умноженной на Ящ, а операция интегрирования эквивалентна делению комплексной амплитуды исходной функции на Ящ.

Применяя метод комплексных амплитуд для бегущей волны вида

 

 

получим выражения для комплексной амплитуды бегущей волны

 

(1.13)

 

1.8 Радиоволны в диэлектрике с потерями энергии

 

Для монохроматических волн удобно записать уравнения Максвелла в комплексном виде:

 

 

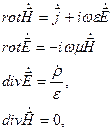
где - комплексные амплитуды соответствующих физических величин.

Комплексная диэлектрическая проницаемость среды.

Учитывая (1.1), запишем для комплексных амплитуд

 

 

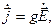
и первое уравнение Максвелла можно представить в виде

 

 

Величину

 

(1.14)

 

называют комплексной диэлектрической проницаемостью среды. Мнимая её часть указывает на свойство среды проводить электрический ток. Величину можно представить в виде вектора на комплексной плоскости (рис.1.4)

 

 

Тангенс угла наклона вектора к горизонтальной оси tgд называют тангенсом угла диэлектрических потерь, который определяется формулой

 

(1.15)

 

Для высококачественных диэлектриков tgд→0

Диэлектрики и проводники

Как следует из (1.14) и (1.15), соотношение между мнимой и действительной частями , т.е. tgд зависит от частоты колебаний. Поскольку плотность тока в среде равна сумме плотности тока проводимости и смещения,

 

 

то величина tgд рана отношению плотности тока проводимости к плотности тока смещения. Таким образом, в одной и той же среде на разных частотах могут преобладать либо только токи проводимости, либо токи смещения, т.е. среда на одних частотах может быть проводником, а на других – диэлектриком.

Если колебания E(t) и H(t) происходят с частотой

 

,

 

то

 

 

и щгр- граничная частота. При частотах, удовлетворяющих условию

щ<< щгр

среда является проводником, а при

щ>> щгр

- диэлектриком.

Комплексная амплитуда напряжённости поля в среде с потерями энергии

Постоянная распространения в в идеальном диэлектрике определяется выражением (1.8), которое с учётом (1.3) принимает вид

 

 

В среде с потерями постоянная распространения становится комплексным числом.

 

 

Комплексную постоянную распространения запишем в виде (см. приложение 4)

 

,

 

где для диэлектрика с малыми потерями

 

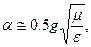
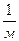.(1.16)

 

Подставив в (1.13) , вместо в, получим

 

(1.17)

 

что эквивалентно записи для мгновенных значений

 

 

Как видим, по мере распространения волны амплитуда колебаний уменьшается по закону

 

.

 

По этой причине б называют коэффициентом затухания среды. Аналогично изменяется и напряжённость магнитного поля

 

 

Средняя во времени мощность электромагнитного поля, проходящая через поверхность единичной площади, определяется усреднённым за период колебаний

 

 

вектором Пойнтинга.

 

 

Подставив сюда E(t,z) и H(t,z), получим

 

 

Итак, в среде с потерями плотность мощности плоской электромагнитной волны уменьшается по мере удаления волны от источника со скоростью

 

, дБ/м

 

1.9 Радиоволны в проводниках. Скин-эффект

 

В радиосистеме радиоволны распространяются либо в свободном пространстве, либо в линиях передачи - направляющих системах. Линия передачи представляет собой совокупность проводников и диэлектрика. Волна распространяется в диэлектрике и попадает на границу раздела диэлектрик-проводник.

В результате возникает волна, отражённая и преломлённая, уходящая вглубь проводника. Можно показать, что в проводниках угол преломления в≈0, независимо от угла падения, т.е. преломленная волна уходит в проводник почти по нормали к границе раздела сред (рис. 1.5)

 

 

На рисунке 1.5: -вектор Пойнтинга падающей волны, - отражённой волны, - преломлённой волны.

На рисунке 1.6 показана часть проводника и направления координатных осей.

 

 

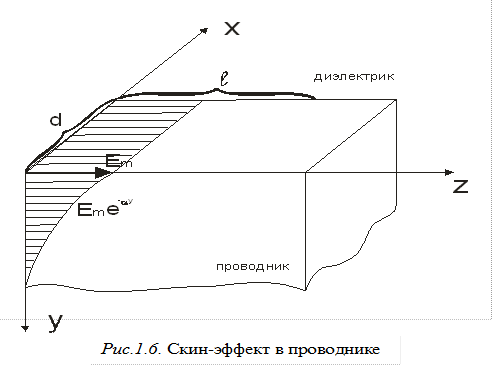
Составляющая напряжённости электрического поля E, касательная к границе раздела сред, имеет на границе амплитуду колебания E . В соответствии с (1.17), комплексная амплитуда зависит от координаты y следующим образом:

 

(1.18)

 

Коэффициент затухания в проводнике (см. приложение 4)

 

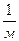(1.19)

 

В проводнике б значительно выше, чем в диэлектрике, поэтому амплитуда колебаний Е быстро уменьшается по мере проникновения поля в глубину проводника. То же действительно и для напряжённости магнитного поля Н. В результате, в проводнике электромагнитное поле расположено в достаточно тонком поверхностном слое.

Глубину проникновения поля в проводнике оценивают глубиной скин-слоя h , т.е. величиной y = h , при которой амплитуда колебаний поля уменьшается в е раз, по сравнению со значением на поверхности. Из (1.18) следует, что глубина скин-слоя

 

(1.20)

 

или, с учётом (1.19)

 

(1.21)

 

где f-частота колебаний поля,

 

 

магнитная проницаемость, g-электропроводность проводника.

Сопротивление проводника переменному ноку.

В результате того, что напряжённость электрического поля сосредоточена вблизи поверхности проводника, переменный электрический ток протекает в относительно узком приповерхностном слое, что следует из закона Ома: 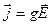. В результате, сопротивление переменному току оказывается выше, чем постоянному.

Получим выражение для сопротивления отрезка проводника длинной l, шириной d и бесконечной глубиной (координата y меняется от 0 до ∞). В соответствии с (1.18), плотность тока

 

 

Комплексная амплитуда тока, проходящего через поперечное сечение проводника шириной б и бесконечной глубиной

 

 

или

 

 

Комплексная амплитуда напряжения на проводнике длиной

 

,

 

Отсюда сопротивление проводника

 

 

Как видим, сопротивление Z имеет действительную часть

 

 

и мнимую часть индуктивного характера

 

 

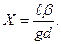
Учитывая (1.20), получим, что активное сопротивление проводника переменному току

 

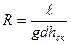(1.22)

 

равно сопротивлению проводника постоянному току, если высота проводника h=hск.

Как следует из (1.22), при изготовлении проводников для переменного тока толщину металлизации нецелесообразно устанавливать существенно больше hск. На практике толщину металлизации выбирают с запасом в пределах h=(2...3)hск

 

2. Радиоволны в линиях передачи

 

Для передачи энергии электромагнитного поля от передатчика к передающей антенне, от приемной антенны к приемнику, от каскада к каскаду в радиосистеме применяют линии передачи. Иначе их называют фидерные линии от английского слова feed– питать. Например, фидерная линия, ведущая от генератора электромагнитных колебаний к антенне – это линия, питающая антенну электромагнитной энергией.

 

2.1 Типы передающих линий

 

В современных радиосистемах используют, в основном, четыре типа передающих линий – двухпроводную, коаксиальную, микрополосковую и волноводную – рис.2.1.

Простейшей линией является двухпроводная – это два параллельных металлических проводника. Если один провод расположен внутри другого, получается коаксиальная линия, или коаксиальный кабель. В каскадах СВЧ применяют микрополосковую линию (МПЛ), а также волноводы – трубы прямоугольного и круглого сечения. МПЛ – это два параллельных проводника - узкий и широкий, разделенных диэлектрической подложкой.

В линиях передачи электромагнитное поле существует в пространстве около проводников, а сами проводники подобны рельсам, задающим направление движения энергии поля.

Пространство между проводниками и линией может быть ничем не заполненным. В этом случае линии являются воздушными. Если между проводниками имеется диэлектрик, то это линия с диэлектрическим заземлением.

Для того, чтобы определить структуру электромагнитного поля в линии передачи, рассмотрим модель, справедливую для всех типов линий – это две параллельные бесконечные плоскости – рис.2.2

 

Решим уравнения Максвелла для линии передачи, образованной двумя параллельными плоскостями, при следующих допущениях:

1) плоскости идеально проводящие, т.е. удельная электропроводность материала плоскости ;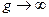

2) диэлектрик между плоскостями идеальный, т.е. его удельная электропроводность ;

ищем решение в виде волн, распространяющихся вдоль оси z;

вдоль оси y плоскости бесконечны и электромагнитное поле вдоль этой оси не меняется;

линия возбуждается источником монохроматического поля.

При сделанных допущениях 1-е и 2-е уравнения Максвелла для комплексных амплитуд имеют следующий вид:

 

 

 

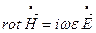
Раскрывая их и учитывая, что производные составляющих поля по оси y равны 0, получим 2 системы уравнений – первая относительно переменных , ,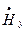

 

,

 

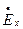; (2.1)

 

,

 

вторая - относительно переменных , ,

 

 

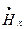(2.2)

 

 

Система уравнений (2.1) описывает поля, у которых вектор напряженности магнитного поля перпендикулярен направлению распространения z, в то время, как вектор 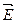имеет проекцию на ось z. Такие поля называют поперечно магнитными, или поля TM – типа (Transverse Magnetic Waves). Иначе их называют полями E – типа.

Система (2.2) относится к поперечно – электрическим полям (Transverse Electrical Waves), т.е. полям ТЕ – типа (или полям H), поскольку здесь вектор напряженности электрического поля 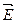перпендикулярен направлению распространения z - рис. 2.3. Рассмотрим структуру полей различных типов более подробно.

2.2 Поперечно- магнитные волны

 

Из системы (2.1) исключим 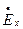и и составим одно уравнение относительно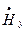

 

(2.3)

 

Получим уравнение эллиптического типа, для однозначного решения которого требуется задание граничных параметров [2].

Рассматриваемая линия передачи ограничена плоскостями, расположенными при следующих значениях координаты x: x = 0 и x = a.

На границе с проводником вектор 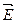расположен таким образом, что может быть представлен суммой нормальной Eн и касательной Eкас составляющих-рис.2.4 диэлектрик.

 

Рис. 2.4. Электрическое поле на границе диэлектрик-проводник.

 

Наличие касательной составляющей электрического поля вызывает появление электрического тока плотностью

 

,

 

где - удельная электропроводность проводника.

Поскольку плотность тока конечна, а проводимость идеального проводника 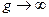, то нужно выполнение условия при x = 0, x = a. В соответствии со вторым – уравнением системы (2.1) граничные условия для уравнения (2.3) запишем следующим образом:

 

, при x = 0, x = a.(2.4)

 

В приложении 5 получено решение уравнения (2.3) с граничными условиями (2.4). При отсутствии отражений оно может быть записано в следующем общем виде:

 

 

где 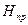- амплитуда напряженности магнитного поля прямой волны при z = 0 (m = 0, 1, 2, 3, …..),

 

,

 

.

 

При выполнении условия 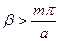имеем

 

,

 

где

,

 

или

 

, (2.5)

 

критическая частота

 

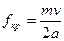. (2.6)

 

В результате поле принимает вид бегущей волны

 

,

 

, (2.7)

 

,

 

где

 

.

 

Таким образом, в линиях передачи возможно существование бесконечного числа поперечно – магнитных волн типа Em, отличающихся числом m, которые распространяются вдоль оси z, если частота колебаний источника f > fкр.

Поперечные электромагнитные волны

Если в выражениях (2.7) и (2.6) установить m = 0, то получим поле, имеющее две взаимно перпендикулярные составляющие 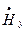и 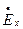. Такое поле называется поперечно электромагнитным, или поле ТЕМ – типа (Transverse Electro-Magnetic).

ТЕМ – волны существуют при любых частотах f, т.е fкр =0 и имеют такую же структуру, как поле в свободном пространстве.

 

2.3 Поперечно – электрические волны

 

Решая уравнения системы (2.2), получим выражение для составляющих поля поперечно электрического типа (ТЕ – или H – волны):

 

,

 

, (2.8)

 

,

 

где - амплитуда колебаний напряженности электрического поля прямой волны при z=0,

 

 

волновое сопротивление среды. Постоянная распространения определяется выражением (2.5), критическая частота fкр - формулой (2.6).

Как видно из (2.8), существует бесконечное число типов поперечно - электрических волн Hm, соответствующих разным m = 1,2,3,… При m = 0, все составляющие поля равны 0.

Так же как и поперечно – магнитные поля, H – волны распространяются вдоль оси z, если частота колебаний источника превышает критическую частоту fкр, определяемую выражением (2.6).

 

2.4 Фазовая и групповая скорости волн. Длина волны в линии

 

Фазовая скорость движения волн типа Em и Hm, т.е скорость распространения гармонических колебаний одной фазы, определяется выражением

 

 

Подставив сюда выражение (2.5) и получим

 

, (2.9)

 

где

 

 

скорость света в среде.

Как видим, фазовая скорость ТМ - и ТЕ – волн всегда больше скорости света. Следует отметить, что фазовая скорость E – и H – волн зависит от частоты колебаний f. Зависимость от f, называется дисперсией, а среда, в которой наблюдается дисперсия – дисперсионной. Таким образом, линии передачи, в которых распространяются поперечно – магнитные или поперечно – электрические волны являются дисперсными.

Помимо фазовой, для характеристики движения радиоволн применяют понятие групповой скорости . Групповая скорость введена для оценки движения радиосигнала.

Радиосигналом называются высокочастотные колебания, модулированные низкочастотными колебаниями, которые содержат информацию. Групповая скорость – это скорость перемещения информации. Одновременно, групповая скорость является скоростью перемещения энергии.

При движении радиосигнала имеем не монохроматическую волну, а волну, содержащую спектр частот. Если радиосигнал узкополосный, т.е. ширина спектра много меньше средней частоты щ, то групповая скорость определяется выражением [1]:

 

(2.10)

 

Выражение (2.10) можно применить и к линиям передачи, определяя тем самым, скорость перемещения энергии.

Если в линии распространяется ТЕМ – волна, для которой 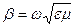, то из (2.10) следует, что

 

,

т.е. равна скорости света v в однородной среде.

При распространении волн Em и Hm в формулу (2.10), вместо в, следует подставить фазовый множитель вm, определяемый выражением (2.5). В результате получим

 

(2.11)

 

Как видим, групповая скорость меньше скорости света в среде v. Объединяя выражения (2.9) и (2.11), запишем

 

(2.12)

 

Длина волны в линии

Как известно, длина волны в линии – это расстояние, проходимое волной за период колебаний T

 

,

 

где v определяется выражением (2.9).

Если в линии распространяется ТЕМ-волна, то фазовая скорость равна скорости света в среде v. Поскольку

 

,

 

,

 

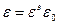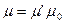скорость света в вакууме, то

 

,

 

где , - относительные диэлектрическая и магнитная проницаемости диэлектрика, заполняющего линию, и длина волны в линии

 

,

 

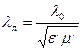где 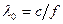- длина волны в вакууме.

В случае распространения волн Em и Hm - типа

 

(2.14)

 

Из соотношений (2.13) и (2.14) следует, что уменьшается при заполнении линии диэлектриком или магнитным материалом, и увеличивается при возбуждении поперечно – магнитных и поперечно – электрических волн.

 

2.6 Затухающие электромагнитные поля

 

Если к линии подключен источник, генерирующий колебания, частота которых меньше критической, определяемой формулой (2.6), то система уравнений (2.1) имеет следующее решение (см. приложение 5):

 

(2.15)

 

где - зависящие от х амплитуды колебаний напряженностей поля в точке z=0

 

 

- действительное число,

 

 

Из (2.15) видно, что амплитуда колебаний, возбуждаемых в линии в точке z=0, уменьшается с ростом z, причем быстрота затухания тем больше, чем сильнее отличаются f от fкр. При любых z колебания синфазны, т.е. отсутствует движение волны.

Как следует из (2.15) колебания H(t) и E(t) происходят с фазовым сдвигом, равным 90 , поэтому средний во времени вектор Пойнтинга равен 0, т.е. электромагнитное поле не переносит энергии.

 

2.7 Радиоволны в прямоугольном волноводе

 

Прямоугольный волновод (рис.2.5) - широко используемая линия передачи, обладающая наименьшими потерями энергии, по сравнению с другими типами линий.

 

 

Поперечным сечением волновода является прямоугольник, широкая сторона которого равна а, узкая-b.

Для нахождения электромагнитного поля внутри волновода следует решить уравнения Максвелла с граничными условиями

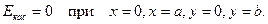
где - касательная составляющая напряженности электрического поля. Проведя преобразования, аналогичные тем, которые были проделаны при нахождении поля между параллельными плоскостями, найдем выражения для составляющих поля в волноводе. Здесь также имеются две группы полей:

- поперечно-электрические или ТЕ-типа (Н-тип),

- поперечно-магнитные или ТМ-типа (Е-тип).

Поле Н-типа имеют составляющие Ех, Еу, Нх, Ну, Нz, а поле Е-типа – Ех, Еу, Еz, Нх, Ну.

Радиоволны Н-типа

Поперечно-электрические поля имеют следующие составляющие:

 

(2.16)

 

(2.17)

 

Как видим, поле имеет вид бегущей волны при , где

 

(2.18)

 

В волноводе может распространяться бесконечное число волн Hmn, соответствующих разным значениям m и n. Для того чтобы расширить диапазон пропускаемых частот, следует, по возможности, уменьшить критическую частоту . С этой целью следует возбуждать волны, у которых m и n минимальны.

Как следует из выражений для составляющих поля, не существует волны Н00. Простейшими типами колебаний являются Н10 и Н01. Так как a>b, то из (2.18) следует, что наименьшая критическая частота у волн Н10. Именно она, главным образом, используется на практике.

Волна Н10

Подставим в (2.16) m=1, n=0, получим

 

 

где -постоянная распространения волн Н10, определяемая выражением (2.16), а критическая частота

 

 

Поскольку

 

,

 

где -критическая длина волны в диэлектрике, заполняющем волновод, то

 

.

 

Длина волны в волноводе определяется соотношением (2.14), справедливым для волн Н- и Е-типа.

На рис.2.6 приведено распределение линий напряженности Е и Н в случае возбуждения волн Н10.

 

 

2.8 Волны ТЕМ-типа

 

Как было отмечено в разделе 2.3, поперечные электромагнитные поля (ТЕМ-типа) существуют в линии при любых частотах колебаний, в том числе при , т.е. при протекании постоянного тока. Поэтому ТЕМ-волны могут распространяться в тех линиях, которые пропускают постоянный ток. Среди представленных на рис.2.1 это - двухпроводные, коаксиальные и микрополосковые линии.

 

На рис.2.7 изображены распределения электрических и магнитных линий в линиях с ТЕМ-волнами, справедливые для некоторого момента времени.

Помимо главной особенности таких ТЕМ-волн - отсутствие граничной частоты, эти волны имеют следующие свойства.

Фазовая скорость не зависит от частоты колебаний и равна скорости света в среде

 

 

где с- скорость света в вакууме. Для немагнитных сред (где )

 

(2.19)

 

В микрополосковой линии среда неоднородна по сечению, поэтому в (2.19) нужно подставить некоторую эффективную относительную диэлектрическую проницаемость , которая заключена в пределах ,где - относительная диэлектрическая проницаемость подложки. Значение для микрополосковых линий можно найти, например в работе .

Длина волны в линии не зависит от частоты колебаний f:

 

 

где - длина волны в вакууме. Для линий с немагнитным заполнением

(2.20)

 

Поскольку структура поля в линии такая же. как и при протекании постоянного тока, а статическое электрическое поле потенциально, то и для переменных полей можно использовать понятие потенциала . Это дает возможность перехода при расчете поля от дифференциальной векторной величины к интегральной скалярной величине , где U – разность потенциалов, или напряжение. В результате, вместо расчёта трех проекций вектора 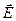, зависящих от 4-х переменных, достаточно найти одну величину U как функцию 2-х переменных. Это значительно упрощает расчёт.

Вектор плотности тока 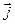в линиях с ТЕМ-волной имеет составляющую, направленную вдоль оси распространения (оси х). Поэтому, вместо дифференциальной векторной величины, можно перейти к интегральной скалярной величине – току I(t,x).

 

2.9 Телеграфные уравнения

 

Получим соотношение между напряжением U и током I в линии передачи с ТЕМ-волной, которые позволят анализировать распространение электромагнитной волны в линии, не решая уравнения Максвелла. С этой целью рассмотрим небольшой отрезок коаксиальной линии длинной 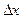(рис.2.8).

Полагаем, что потенциал в сечении А равен ц , а в сечении В ц2. Линию считаем не имеющей потерь, обладающей погонной индуктивностью L1 и погонной емкостью С1 (L1, C1-это соответственно индуктивность и емкость линии длиною 1м).

 

 

Воспользуемся интегральной записью II уравнения Максве

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: