 |
Классификация точек разрыва
|
|
|
|
ВВедение
В данном методическом пособии приводятся подробные решения основных типовых задач и упражнений по всем разделам математического анализа, которые изучаются в общем курсе «Высшая математика». Студентам-заочникам рекомендуется тщательно разобрать все примеры и придерживаться предложенных алгоритмов при выполнении заданий первой индивидуальной домашней контрольной работы из [10]. Студенты дневного отделения могут использовать данные указания при решении домашних упражнений в течение семестра, а также при подготовке к контрольным работам и экзамену.
Дополнительную информацию теоретического характера можно найти в учебниках [5]–[7] (по всем разделам), а также в [9] (для §§1–2, пп. 3.1, 3.2, 4.1–4.4, 5.1–5.5). Решения задач, не вошедших в данное пособие, имеются в [1] –[4] и в [8].
Вычисление пределов
1.1. Основные теоретические положения. Вычисление пределов опирается на свойства бесконечно малых и бесконечно больших функций и основные теоремы об арифметическихдействиях с пределами. Используется также один из известных замечательных пределов:
 (1.1.)
(1.1.)
Следует учитывать и теорему о пределе сложной функции. В частности, в силу этого утверждения
 (1.2)
(1.2)
Пусть  ,
,  . При вычислении предела алгебраической суммы функций возможны ситуации:
. При вычислении предела алгебраической суммы функций возможны ситуации:
1)если A и B – конечные числа, тогда  (по теореме о пределе алгебраической суммы);
(по теореме о пределе алгебраической суммы);
2) если один из пределов (A или B) конечен, а другой является одним из бесконечных символов, то  (в силу свойств бесконечно больших функций);
(в силу свойств бесконечно больших функций);
3) в случае, когда f(x) и g(x) – бесконечно большие функции одного знака, то  ; если же f(x) и g(x) – бесконечно большие функции разных знаков, то ничего конкретного (в общей ситуации) утверждать нельзя, поэтому говорят о неопределенности вида
; если же f(x) и g(x) – бесконечно большие функции разных знаков, то ничего конкретного (в общей ситуации) утверждать нельзя, поэтому говорят о неопределенности вида  , требующей дополнительного исследования.
, требующей дополнительного исследования.
|
|
|
Вычисляя предел произведения функций, необходимо учитывать следующее:
1) если A и B – конечные числа, то  (по теореме о пределе произведения);
(по теореме о пределе произведения);
2) если один из пределов (A или B) конечен и отличен от нуля(!), а другой является одним из бесконечных символов, то  (по свойству бесконечно больших функций);
(по свойству бесконечно больших функций);
3) если один из пределов равен нулю, а второй является одним из бесконечных символов, то говорят о неопределенности вида  .
.
Наконец, при вычислении пределов частного применяются такие правила:
1) если A и B – конечные числа, причем B¹0, то  (по теореме о пределе частного);
(по теореме о пределе частного);
2) если A и B – конечные числа, причем A¹0, B=0, то  (так как функция 1/g(x) при этом является бесконечно большой при
(так как функция 1/g(x) при этом является бесконечно большой при  и остается воспользоваться свойствами бесконечно больших функций);
и остается воспользоваться свойствами бесконечно больших функций);
3) если  , а B – любое конечное число, то
, а B – любое конечное число, то  , а если
, а если  , а А – любое конечное число, то
, а А – любое конечное число, то  (в силу свойств бесконечно больших функций);
(в силу свойств бесконечно больших функций);
4) наконец, если A=B=0, то говорят о неопределенности вида  , а если A и B – бесконечные символы, то о неопределенности вида
, а если A и B – бесконечные символы, то о неопределенности вида  .
.
1.2. Раскрытие неопределенностей вида  . В данном случае в числителе и знаменателе рекомендуется вынести за скобки слагаемое, которое растет быстрее других (для многочленов, в частности, это слагаемое, имеющее старшую степень). В результате алгебраическая сумма представляется в виде произведения бесконечно большой функции на функцию, имеющую конечный и отличный от нуля предел.
. В данном случае в числителе и знаменателе рекомендуется вынести за скобки слагаемое, которое растет быстрее других (для многочленов, в частности, это слагаемое, имеющее старшую степень). В результате алгебраическая сумма представляется в виде произведения бесконечно большой функции на функцию, имеющую конечный и отличный от нуля предел.
Пример 1.1. Вычислить  .
.
Решение. Предел последовательности можно рассматривать как частный случай предела функции. Очевидно, что в силу свойств бесконечно больших функций при  и
и  . Поэтому имеем неопределенность вида
. Поэтому имеем неопределенность вида  . Проведем подготовительные преобразования:
. Проведем подготовительные преобразования:
 ;
;  .
.
Далее получаем:
 .
.
Последнее равенство справедливо в силу теорем о пределе суммы и частного функций с учетом того, что все слагаемые, кроме единиц, являются бесконечно малыми (по теореме о связи между бесконечно большой и бесконечно малой функциями).
|
|
|
1.3. Раскрытие неопределенностей вида  . Неопределенности такого вида возникают, как правило, либо при исследовании разности двух дробей (в этом случае рекомендуется приводить дроби к общему знаменателю), либо при рассмотрении разности иррациональных выражений (для избавления от иррациональностей следует преобразовать исходное выражение либо к разности квадратов, либо к сумме или разности кубов). Далее задача сводится к рассмотренной выше неопределенности вида
. Неопределенности такого вида возникают, как правило, либо при исследовании разности двух дробей (в этом случае рекомендуется приводить дроби к общему знаменателю), либо при рассмотрении разности иррациональных выражений (для избавления от иррациональностей следует преобразовать исходное выражение либо к разности квадратов, либо к сумме или разности кубов). Далее задача сводится к рассмотренной выше неопределенности вида  .
.
Пример 1.2. Вычислить  .
.
Решение. В данном случае, чтобы раскрыть неопределенность  , необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Для
, необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Для  таким «сопряженным» является
таким «сопряженным» является  . Таким образом, получаем:
. Таким образом, получаем:
 .
.
Таким образом, мы попали в ситуацию, разобранную при решении примера 1.1. Проведем соответствующие преобразования в знаменателе:
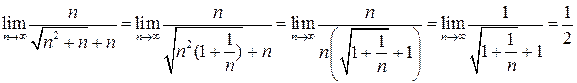 .
.
Итак,  .
.
1.4. Раскрытие неопределенностей вида  . В этой ситуации основная цель преобразований – выделить в числителе и знаменателе множители вида (x-a) (именно они при вычислении предела при
. В этой ситуации основная цель преобразований – выделить в числителе и знаменателе множители вида (x-a) (именно они при вычислении предела при  "обеспечивают" наличие неопределенности).
"обеспечивают" наличие неопределенности).
Пример 1.3. Вычислить  .
.
Решение. Подставляя предельное значение x=3 в числитель и знаменатель, получаем, что оба выражения обращаются при этом в нуль. Стоящие в числителе и знаменателе многочлены можно разложить на множители, причем в числителе достаточно воспользоваться формулой разности квадратов, а в знаменателе необходимо предварительно найти корни соответствующего квадратного трехчлена. Следует помнить, что если  – корни квадратного трехчлена
– корни квадратного трехчлена  , то справедлива формула
, то справедлива формула
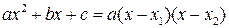 , (1.3)
, (1.3)
а для трехчлена 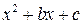 выполняется равенство
выполняется равенство
 . (1.4)
. (1.4)
Таким образом, имеем:
 .
.
Пример 1.4. Вычислить 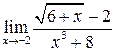
Решение. Подставляя предельное значение x=2 в числитель и знаменатель, получаем, что оба выражения обращаются в нуль. Знаменатель представляет собой «сумму кубов», поэтому при разложении его на множители получаем:  . После умножения числителя и знаменателя на сопряженное числителю выражение
. После умножения числителя и знаменателя на сопряженное числителю выражение  , имеем:
, имеем:

При вычислении пределов тригонометрических функций применяются «замечательные пределы» (1.1) и (1.2).
|
|
|
Пример 1.5. Вычислить а)  ; б)
; б)  ; в)
; в)  .
.
Решение. В случае а) очевидно, что при 
 и
и 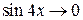 . Чтобы применить (1.2), необходимо получить в знаменателе выражение, совпадающие с аргументом синуса. Для этого числитель и знаменатель умножаем на число «4»:
. Чтобы применить (1.2), необходимо получить в знаменателе выражение, совпадающие с аргументом синуса. Для этого числитель и знаменатель умножаем на число «4»:
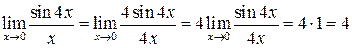 .
.
Однако на практике оказывается полезной теорема, согласно которой в произведении и в частном эквивалентные функции (т.е. те, для которых выполняется равенство  ) можно заменять друг другом. В частности,
) можно заменять друг другом. В частности,
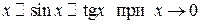 ;
;  . (1.5)
. (1.5)
Поэтому решение а) можно записать в следующем виде:  .
.
В случае б) знаменатель разложим на множители как «разность квадратов», а в числителе воспользуемся одним из соотношений (1.5):
 .
.
В задании в) необходимо сначала преобразовать числитель в произведение, используя формулу разности синусов, а потом применить эквивалентные соотношения из (1.5), учитывая, что 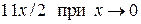 :
:

Замечание. Другие примеры на вычисление пределов можно найти в [1, стр.6-9] и в [3, стр.7-18].
Классификация точек разрыва
При решении задач используются следующие определения.
Точка x=a называется точкой устранимого разрыва функции y=f(x), если выполняется одно из условий: 1) a не принадлежит области определения данной функции, но существует конечный  ; 2) a принадлежит области определения данной функции, существует конечный
; 2) a принадлежит области определения данной функции, существует конечный  , но
, но  .
.
Точка x=a называется точкой разрыва первого рода функции y=f(x), если  не существует, но существуют конечные, различные между собой односторонние пределы
не существует, но существуют конечные, различные между собой односторонние пределы  и
и 
Точка x=a называется точкой разрыва второго рода функции y=f(x), если хотя бы один из односторонних пределов  ,
,  равен бесконечности или не существует.
равен бесконечности или не существует.
При определении характера разрыва в точке x=a необходимо сначала найти  . Если этот предел существует, то x=a окажется (в зависимости от значения предела) либо точкой устранимого разрыва, либо точкой разрыва второго рода. Если
. Если этот предел существует, то x=a окажется (в зависимости от значения предела) либо точкой устранимого разрыва, либо точкой разрыва второго рода. Если  не существует, то находят односторонние пределы – в зависимости от них x=a будет точкой разрыва первого или второго рода.
не существует, то находят односторонние пределы – в зависимости от них x=a будет точкой разрыва первого или второго рода.
Пример 2.1. Найти и классифицировать точки разрыва функции  .
.
Решение. 1)Выражения, стоящие в числителе и знаменателе, непрерывны при всех вещественных x. Однако знаменатель обращается в нуль при x=0 и x=-1, т.е. эти точки не принадлежат области определения и являются точками разрыва. Исследуем каждую из них.
|
|
|
2) Рассмотрим x=0. Так как  , а рассматриваемая точка не принадлежит области определения, заключаем, что x=0 – точка устранимого разрыва.
, а рассматриваемая точка не принадлежит области определения, заключаем, что x=0 – точка устранимого разрыва.
3) Пусть теперь x=-1. Так как при 
 , а
, а 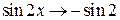 , то заключаем, что
, то заключаем, что  . Следовательно, x=-1 – точка разрыва второго рода.
. Следовательно, x=-1 – точка разрыва второго рода.
Замечание. Другие примеры, связанные с определением характера разрыва, можно найти в [1, стр.10-11].
Дифференцирование функций
3.1. Правила дифференцирования функций одного переменного. При нахождении производных и дифференциалов функции  применяются следующие правила:
применяются следующие правила:
 ; (3.1)
; (3.1)
 ; (3.2)
; (3.2)
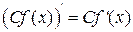 ; (3.3)
; (3.3)
 . (3.4)
. (3.4)
Заметим, что (3.3) следует из (3.2), так как производная константы всегда равна нулю ( ).
).
Чтобы найти производную функции  в точке
в точке  , необходимо сначала найти
, необходимо сначала найти  , а затем в полученное выражение подставить заданное значение.
, а затем в полученное выражение подставить заданное значение.
Необходимо также знать таблицу производных основных элементарных функций. В Таблице 1 формулы приводятся как для функции независимого аргумента  , так и для сложной функции
, так и для сложной функции  .
.
Таблица 1
1)  , ,  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  ,
7) ,
7)  8)
8)  ,
9) ,
9)  10)
10)  11)
11)  12)
12)  13)
13) 
| 1¢)  2¢)
2¢)  3¢)
3¢)  4¢)
4¢)  5¢)
5¢)  6¢)
6¢)  ,
7¢) ,
7¢)  8¢)
8¢) 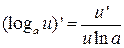 ,
9¢) ,
9¢)  10¢)
10¢)  11¢)
11¢)  12¢)
12¢)  13¢)
13¢) 
|
Дифференциал функции  в произвольной точке задается формулой
в произвольной точке задается формулой
 , (3.5)
, (3.5)
а в фиксированной точке формулой
 . (3.6)
. (3.6)
Для определения производной второго порядка используем правило
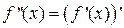 . (3.7)
. (3.7)
Пример 3.1. Найти производную  для
для  и выписать дифференциал этой функции.
и выписать дифференциал этой функции.
Решение. Данную функцию можно представить в виде  , где
, где  , и воспользоваться формулой 9¢) из Табл.1. Далее к числителю полученного выражения применяем (3.1), а функцию
, и воспользоваться формулой 9¢) из Табл.1. Далее к числителю полученного выражения применяем (3.1), а функцию  также рассматриваем как сложную и находим ее производную с помощью 4¢):
также рассматриваем как сложную и находим ее производную с помощью 4¢):

Итак,  , а
, а 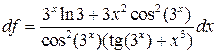 (в силу (3.5)).
(в силу (3.5)).
Пример 3.2. Найти производную функции  в точке x=2.
в точке x=2.
Решение. Функция представляет собой частное, поэтому применяем (3.4), а также формулу производной степенной функции (для  и для
и для  ):
):

Вычисляем производную в заданной точке, для этого подставляем в найденное выражение значение x=2:
 .
.
Пример 3.3. Найти дифференциал функции  в произвольной точке и в точке x=p/2.
в произвольной точке и в точке x=p/2.
Решение. Сначала найдем первую производную исходной функции, воспользовавшись формулами 7¢), (3.4) и 2):

Далее вычисляем производную в точке x=p/2. Поскольку 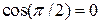 и
и  , то
, то  . В силу (3.6)
. В силу (3.6)  .
.
Пример 3.4. Найти вторую производную функции 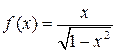 .
.
Решение. Сначала найдем  и обязательно упростим полученное выражение:
и обязательно упростим полученное выражение:

Теперь в силу (3.7) и 1¢) получаем:
 .
.
3.2. Правило Лопиталя вычисления пределов. Если при вычислении пределов затруднительно использование эквивалентностей, то можно применить следующее утверждение.
|
|
|
Правило Лопиталя. Пусть функции f(x) и g(x) определены и дифференцируемы в окрестности точки a, а также являются одновременно бесконечно малыми (или бесконечно большими) при  . Пусть, далее,
. Пусть, далее,  в окрестности точки a (кроме, возможно, самой точки). Если существует
в окрестности точки a (кроме, возможно, самой точки). Если существует  , то существует и
, то существует и  , причем
, причем  .
.
Пример 3.5. Найти с помощью правила Лопиталя:
а)  ; б)
; б) 
Решение. a) В данном случае после подстановки x=0 замечаем, что и числитель, и знаменатель дроби обращаются в нуль, т.е. мы имеем дело с неопределенностью  . Однако использовать замечательные пределы и перейти к эквивалентным функциям нельзя, так как в числителе – сумма. Воспользуемся правилом Лопиталя, предварительно проверив все условия.
. Однако использовать замечательные пределы и перейти к эквивалентным функциям нельзя, так как в числителе – сумма. Воспользуемся правилом Лопиталя, предварительно проверив все условия.
Неопределенность  уже отмечена. Функции, стоящие в числителе и знаменателе, дифференцируемы при всех вещественных x и
уже отмечена. Функции, стоящие в числителе и знаменателе, дифференцируемы при всех вещественных x и  при
при  . В силу сформулированного выше утверждения, если в этом случае существует предел отношения производных, то его значение совпадет со значением искомого предела. Предположим, что это так, и проведем вычисления:
. В силу сформулированного выше утверждения, если в этом случае существует предел отношения производных, то его значение совпадет со значением искомого предела. Предположим, что это так, и проведем вычисления:

Итак, 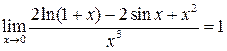
При решении этого примера правило Лопиталя фактически было применено трижды (в тех местах, где над знаком равенства указан вид неопределенности). При этом для обеспечения строгости рассуждений необходимо каждый раз проверять условия сформулированного выше утверждения.
Рассмотрим теперь задание б). Очевидно, что здесь вообще нет эквивалнетных функций. Кроме того, при 
 и
и  . Это неопределенность вида
. Это неопределенность вида  , к которой правило Лопиталя не применяется, однако можно учесть, что если f(x) – бесконечно малая при
, к которой правило Лопиталя не применяется, однако можно учесть, что если f(x) – бесконечно малая при  функция, то 1/f(x) будет бесконечно большой при
функция, то 1/f(x) будет бесконечно большой при  . Поскольку
. Поскольку
 ,
,
то мы приходим к неопределенности  и далее действуем так, как при решении задания а). Обе функции требуемым условиям удовлетворяют, поэтому
и далее действуем так, как при решении задания а). Обе функции требуемым условиям удовлетворяют, поэтому

(учтено, что  ). Итак,
). Итак,  .
.
3.3. Правила дифференцирования функций двух переменных. При дифференцировании функции  по одной из независимых переменных вторая фиксируется и считается константой (это следует из определения частных производных первого порядка). Применяются уже знакомые правила (.3.1)-(3.4) и формулы из табл.1, однако при записи обязательно указывается, по какой переменной происходит дифференцирование. Так, для производной по x используются обозначения
по одной из независимых переменных вторая фиксируется и считается константой (это следует из определения частных производных первого порядка). Применяются уже знакомые правила (.3.1)-(3.4) и формулы из табл.1, однако при записи обязательно указывается, по какой переменной происходит дифференцирование. Так, для производной по x используются обозначения  или
или  . Аналогично запись
. Аналогично запись 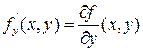 обозначает производную по y.
обозначает производную по y.
Для полного дифференциала первого порядка функции  имеем:
имеем:
 ; (3.8)
; (3.8)
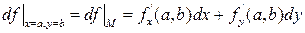 . (3.9)
. (3.9)
Частные производные второго порядка  определяются по формулам
определяются по формулам
 ;
;  ; (3.10)
; (3.10)
 ;
;  . (3.11)
. (3.11)
Заметим, что если исходная функция удовлетворяет некоторым дополнительным свойствам, то справедливо равенство  В этом случае говорят, что «смешанные производные второго порядка» совпадают, или «смешанная производная не зависит от порядка дифференцирования».
В этом случае говорят, что «смешанные производные второго порядка» совпадают, или «смешанная производная не зависит от порядка дифференцирования».
Справедлива формула для полного дифференциала второго порядка функции  :
:
 (3.12)
(3.12)
Пример 3.6. Найти частные производные первого порядка и выписать дифференциал первого порядка функции 
Решение. Чтобы найти  , необходимо зафиксировать переменную y. Воспользовавшись формулой 3¢) из Табл.1, а также (3.1) и (3.3), получим:
, необходимо зафиксировать переменную y. Воспользовавшись формулой 3¢) из Табл.1, а также (3.1) и (3.3), получим:

В данном случае числовой коэффициент и переменная y выступали в роли констант: во втором слагаемом они были вынесены за скобки при дифференцировании, а третье слагаемое от x не зависело – поэтому его производная по x равна нулю.
Аналогично поступаем и с  , только теперь фиксируется переменная y:
, только теперь фиксируется переменная y:

Чтобы выписать дифференциал первого порядка, воспользуемся (3.8.):

Пример 3.7. Найти частные производные второго порядка функции  . Выписать
. Выписать 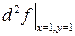 .
.
Решение. Сначала находим частные производные первого порядка. Следует обратить внимание на то, что при фиксированном y функция представляет собой произведение двух функций, зависящих от x, а при фиксированном x это константа, умноженная на функцию от y. Применяя известные уже приемы дифференцирования, получаем:

 .
.
Теперь воспользуемся формулами (3.10) и любой из формул (3.11).

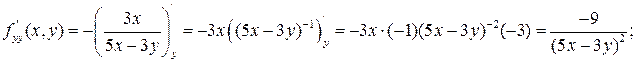

В качестве проверки можно найти вторую смешанную производную и убедиться, что результаты совпадают:

Чтобы записать теперь дифференциал второго порядка в заданной точке (1;1), вычислим значения производных в этой точке, а затем применим (3.12):
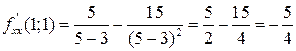 ;
;  ;
;  ;
;
 .
.
3.4. Производная по направлению и градиент. Пусть  — функция двух переменных, определенная в некоторой области D, M(x,y) – произвольная точка этой области,
— функция двух переменных, определенная в некоторой области D, M(x,y) – произвольная точка этой области,  – некоторое направление (вектор, соединяющий
– некоторое направление (вектор, соединяющий
 Рис.1
Рис.1
| начало координат с точкой (a,b) и передвинутый параллельным переносом из начала координат в точку M). Через a и b обозначим углы, образованные вектором направления с положительными направлениями осей OX и OY.
Так как (см. рис. 1) 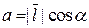 , ,  то справедливы формулы то справедливы формулы
 , ,  . (3.13)
При этом . (3.13)
При этом  и и  называются «направляющими косинусами».: называются «направляющими косинусами».:
|
Производная функции  по направлению
по направлению  в точке M задает скорость изменения функции в этом направлении и может быть найдена по формуле
в точке M задает скорость изменения функции в этом направлении и может быть найдена по формуле
 . (3.14)
. (3.14)
Градиентом функции  в точке M называют вектор с координатами, равными значениям частных производных первого порядка в этой точке:
в точке M называют вектор с координатами, равными значениям частных производных первого порядка в этой точке:
 . (3.15)
. (3.15)
Он определяет направление наискорейшего возрастания функции, а его величина, которую находят по формуле
 , (3.16)
, (3.16)
совпадает с максимальной скоростью возрастания функции в данной точке.
Пример 3.7. Пусть  . Найти градиент функции в точке M(3;1), величину градиента функции в этой точке и производную функции в той же точке по направлению
. Найти градиент функции в точке M(3;1), величину градиента функции в этой точке и производную функции в той же точке по направлению  .
.
Решение. Предварительно находим частные производные функции первого порядка и их значения в заданной точке:

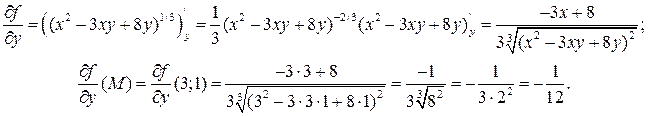
Теперь воспользуемся формулами (3.15) и (3.16):
 ;
;  .
.
Далее,  , поэтому в силу (3.13)
, поэтому в силу (3.13)  ,
,  , и в силу (3.14):
, и в силу (3.14):
 .
.
Замечание. Решение других задач, связанных с дифференцированием, можно найти в [1, стр.12-14], [2, стр.18-22], [3, стр.22-27], [4, стр.14-16].
Исследование функций
4.1. Интервалы монотонности и точки экстремума функции  . Как известно, характер монотонности функции на числовом интервале (a,b) связан со знаком ее производной на этом интервале (если
. Как известно, характер монотонности функции на числовом интервале (a,b) связан со знаком ее производной на этом интервале (если  при всех x из (a,b), то функция возрастает, а если
при всех x из (a,b), то функция возрастает, а если  при всех x из (a,b), то убывает). Далее, пусть X – область определения функции
при всех x из (a,b), то убывает). Далее, пусть X – область определения функции  и
и 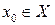 . Если для всех x из некоторой окрестности точки
. Если для всех x из некоторой окрестности точки  выполняется неравенство
выполняется неравенство 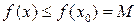 (или
(или 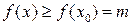 ), то число M (m) называется локальным максимумом (локальным минимумом) функции
), то число M (m) называется локальным максимумом (локальным минимумом) функции  , а сама точка
, а сама точка  - точкой локального максимума (локального минимума). Оба числа объединяются термином «экстремум функции» (соответственно, говорят и о «точках экстремума»).
- точкой локального максимума (локального минимума). Оба числа объединяются термином «экстремум функции» (соответственно, говорят и о «точках экстремума»).
При решении задач на поиск экстремумов функции одного переменного придерживаются следующей схемы рассуждений.
1) Установить область определения функции  .
.
2) Найти ее первую производную.
3) Выяснить, в каких точках из области определения производная обращается в нуль (т.е. решить уравнение f’(x) = 0) Такие точки называются стационарными. Найти значения x, при которых функция определена, а производная – нет (эти точки в дальнейшем называются критическими).
4) Определить знак производной на числовых интервалах, на которые стационарные и критические точки разбили область определения, сделать выводы о характере монотонности.
5) Если при переходе через найденную точку  производная знак не меняет, то
производная знак не меняет, то  не является точкой экстремума; если в окрестности точки
не является точкой экстремума; если в окрестности точки  слева от нее
слева от нее  , а справа
, а справа  , то
, то  - точка максимума исходной функции и
- точка максимума исходной функции и  ; если же в окрестности
; если же в окрестности 
 слева и
слева и  справа, то
справа, то  - точка минимума исходной функции и
- точка минимума исходной функции и  .
.
Пример 4.1. Найти интервалы монотонности и экстремумы функции  .
.
Решение. Данная функция определена для всех действительных чисел, ее производная имеет вид  и также определена при всех x. Из уравнения
и также определена при всех x. Из уравнения  находим стационарные точки:
находим стационарные точки:  ,
,  . Составляем таблицу для числовых интервалов и определяем знак производной. Для этого, наряду с другими способами, можно ограничиться вычислением значения производной в промежуточных точках полученных интервалов. Например,
. Составляем таблицу для числовых интервалов и определяем знак производной. Для этого, наряду с другими способами, можно ограничиться вычислением значения производной в промежуточных точках полученных интервалов. Например,  ,
, 
 . Считаем также значения функции в найденных точках:
. Считаем также значения функции в найденных точках:  ,
,  . Данные собираем в таблицу, в последней строке которой указываем характер монотонности функции:
. Данные собираем в таблицу, в последней строке которой указываем характер монотонности функции:
| X | 
| – 1 | 
| 
| |

| — | + | — | ||
| Поведение f(x) | 
| -2 | 
| 
| |
| Вывод | Убыв. | Т мин. | Возр. | Т. макс. | Убыв. |
Итак, f возрастает на интервале  , убывает на интервалах
, убывает на интервалах  и
и  , имеет точку локального минимума x=-1 (при этом
, имеет точку локального минимума x=-1 (при этом 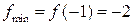 ) и точку локального максимума x=1 (
) и точку локального максимума x=1 ( ).
).
Пример 4.2 Найти экстремумы функции  .
.
Решение. Данная функция определена для всех действительных чисел, кроме x=-2. Дифференцируя частное, получаем, что  . Очевидно, что производная также определена при всех x, кроме x=-2 (критическая точка). Из уравнения
. Очевидно, что производная также определена при всех x, кроме x=-2 (критическая точка). Из уравнения  находим стационарные точки:
находим стационарные точки:  ,
,  . Составляем, как и выше, таблицу для числовых интервалов и устанавливаем знаки производной (можно заметить, что знаменатель всегда положителен, а потому знак производной зависит только от числителя). Определяем также значения функции в найденных точках и собираем данные в таблицу.
. Составляем, как и выше, таблицу для числовых интервалов и устанавливаем знаки производной (можно заметить, что знаменатель всегда положителен, а потому знак производной зависит только от числителя). Определяем также значения функции в найденных точках и собираем данные в таблицу.
| x | 
| – 4 | 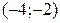
| -2 | (-2,0) | 
| |

| + | — | Не сущ. | — | + | ||
| Повед. f(x) | 
| -8 | 
| Не сущ. | 
| 
| |
| Вывод | Возр. | Т макс. | Убыв. | Убыв. | Т. мин. | Возр. |
Таким образом, x=-4 – точка локального максимума и  , x=0 – точка локального минимума (
, x=0 – точка локального минимума (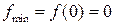 ).
).
Следует обратить внимание на то, что данный пример иллюстрирует «локальность» экстремума (в частности, оказывается, что  ).
).
Пример 4.3. Найти экстремумы функции  .
.
Решение. Данная функция определена для всех действительных чисел, ее производная имеет вид  . При этом производная не определена там, где в нуль обращается знаменатель, т.е. при x=0. Эта точка является критической. Стационарных точек нет, так как в числителе стоит постоянное число, и потому дробь не обращается в нуль. Учитывая, что знак производной совпад
. При этом производная не определена там, где в нуль обращается знаменатель, т.е. при x=0. Эта точка является критической. Стационарных точек нет, так как в числителе стоит постоянное число, и потому дробь не обращается в нуль. Учитывая, что знак производной совпад
|
|
|


