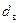|
Задания для самостоятельной работы.
|
|
|
|
Задача 2. Изучается влияние стоимости основных x1 и оборотных x2 средств на величину валового дохода y торговых предприятий. Для этого по 12 торговым предприятиям были получены данные, приведенные в таблице 2.2 (все величины измеряются в млн. руб.).
Табл. 2.2
| Номер варианта | Переменные | Номер предприятия | |||||||||||
| x1 | 3,9 | 4,8 | 3,9 | 4,3 | 4,8 | 4,9 | 5,6 | 4,6 | 5,6 | 7,2 | 7,7 | ||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 3,9 | 4,1 | 3,8 | 4,7 | 4,4 | 5,2 | 5,6 | 5,2 | 5,5 | 6,8 | 7,5 | 7,2 | |
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,3 | 4,9 | 4,4 | 4,9 | 6,3 | 4,8 | 6,2 | 7,7 | 7,6 | 7,1 | |||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,7 | 4,2 | 3,8 | 4,1 | 5,5 | 5,8 | 5,7 | 7,6 | 7,6 | 7,4 | |||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,4 | 4,4 | 4,2 | 4,2 | 4,1 | 5,1 | 5,7 | 4,8 | 5,6 | 7,6 | 7,7 | ||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,5 | 4,7 | 4,3 | 4,2 | 4,8 | 5,7 | 5,5 | 5,2 | 5,8 | 7,2 | 7,1 | 7,2 | |
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,3 | 4,2 | 4,5 | 4,2 | 5,5 | 6,3 | 4,8 | 5,4 | 7,1 | 7,9 | |||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,1 | 4,2 | 4,6 | 5,1 | 6,2 | 4,9 | 6,2 | 7,5 | 7,4 | ||||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 3,9 | 4,1 | 3,8 | 4,8 | 5,6 | 5,6 | 4,8 | 7,6 | 6,9 | 7,4 | |||
| x2 | |||||||||||||
| y | |||||||||||||
| x1 | 4,9 | 4,2 | 4,6 | 4,2 | 3,8 | 4,9 | 5,4 | 5,3 | 5,4 | 7,4 | 7,6 | 6,9 | |
| x2 | |||||||||||||
| y |
Требуется:
|
|
|
1. Полагая, что между переменными y, x1, x2существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии yпо x1и x2) и пояснить экономический смысл параметров регрессии.
2. Установить раздельное влияние на величину валового дохода двух факторов - основных и оборотных средств через стандартизованные коэффициенты регрессии и средние коэффициенты эластичности.
3. Проверить значимость коэффициентов регрессии и построить для них 95% доверительные интервалы.
4. Сравнить значения скорректированного и не скорректированного коэффициентов множественной детерминации и проверить значимость полученного уравнения регрессии по 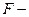 критерию на уровне
критерию на уровне  = 0,05.
= 0,05.
5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1после x2, и фактора x2после x1.
Тема 3. Временные ряды
Расчетные формулы.
3.1.
3.1. Выборочный коэффициент автокорреляции  го порядка:
го порядка:
 .
.
3.2. Выборочная автокорреляционная функция:

3.3. Коррелограмма – график выборочной автокорреляционной функции 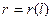 .
.
|
|
|
|
|


|

|

|
На рис. 3.1 чередуются затухающие положительные и отрицательные значения 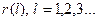 . Это характерно для стационарного ряда.
. Это характерно для стационарного ряда.
Наблюдаются незначительные, малые значения 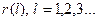 близкие к нулю. Это полностью случайный ряд без тренда и циклических компонент (рис. 3.2).
близкие к нулю. Это полностью случайный ряд без тренда и циклических компонент (рис. 3.2).
На рис. 3.3 коррелограмма представляет убывание положительных значений 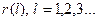 . Здесь ряд имеет тренд и не является стационарным.
. Здесь ряд имеет тренд и не является стационарным.
|
|
|
Если на коррелограмме после периода затухания имеется одно или несколько сравнительно больших по абсолютной величине значений  , то ряд помимо тренда имеет циклическую компоненту с периодом
, то ряд помимо тренда имеет циклическую компоненту с периодом  (рис. 3.4).
(рис. 3.4).
Моделирование тенденции ряда непосредственно по исходным данным выполняется только в том случае, когда отсутствует циклическая компонента ряда.
Аналитическое выравнивание
3.4. Для аналитического выравнивания (сглаживания) временного ряда используются различные модели тренда:
- линейный  ;
;
- параболический  ;
;
- гиперболический  и т.д.
и т.д.
3.5. Факторная сумма квадратов:
 .
.
3.6. Остаточная сумма квадратов:
 .
.
3.7. 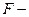 статистика Фишера:
статистика Фишера:
 ,
,
Механическое выравнивание
3.8. В методе скользящей средней для интервала сглаживания с нечетным числом точек среднее значение ряда находится по формуле:
 .
.
Для интервала сглаживания с четным числом точек вначале находятся скользящие средние

для промежуточных значений уровней ряда, а затем выполняется центрирование скользящих средних

для приведения их к фактическим значениям уровней исходного ряда.
В любом случае в методе скользящей средней число уровней сглаженного ряда уменьшается на  значений по сравнению с исходным рядом.
значений по сравнению с исходным рядом.
3.9. Критерий Дарбина-Уотсона
 .
.
3.10. Выборочный коэффициент автокорреляции
 .
.
3.11. Из таблиц теста Дарбина-Уотсона при заданном уровне значимости 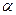 , количестве наблюдений
, количестве наблюдений 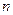 и числе объясняющих переменных
и числе объясняющих переменных  находятся два критических значения:
находятся два критических значения:  . Возможны следующие случаи:
. Возможны следующие случаи:
- если  , то имеется положительная автокорреляция;
, то имеется положительная автокорреляция;
- если  , то имеется отрицательная автокорреляция;
, то имеется отрицательная автокорреляция;
- если 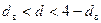 , то признается отсутствие автокорреляции;
, то признается отсутствие автокорреляции;
- если  или
или  , то тест ответа не даёт.
, то тест ответа не даёт.
|

|

|

|


 зона зона
зона зона
неопредел. неопредел.
 | ||||||||||||||||||||
|
|
|
| |||||||||||||||||
Решение типовой задачи.
В таблице 3.1 приводятся данные об объеме инвестиций ( , млн. долл.) за последние 16 лет по одному из регионов страны.
, млн. долл.) за последние 16 лет по одному из регионов страны.
Табл. 3.1

| ||||||||

| 1,72 | 3,57 | 7,45 | 8,59 | 9,52 | 10,66 | 10,55 | 15,14 |

| ||||||||

| 17,05 | 20,46 | 20,03 | 27,52 | 31,72 | 36,34 | 42,59 | 43,51 |
Требуется:
|
|
|
1. Найти выборочные коэффициенты автокорреляции до 4-го порядка включительно, построить коррелограмму и по коррелограмме выявить тип процесса.
2. Полагая тренд линейным, найти его уравнение и проверить значимость полученного уравнения по 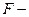 критерию на уровне значимости
критерию на уровне значимости  .
.
3. Выполнить сглаживание временного ряда с интервалами сглаживания  и
и  года.
года.
4. На уровне значимости  выявить наличие или отсутствие автокорреляции возмущений, используя критерий Дарбина-Уотсона.
выявить наличие или отсутствие автокорреляции возмущений, используя критерий Дарбина-Уотсона.
Решение выполним в среде MS Excel.
1. Вычислим выборочные коэффициенты автокорреляции до 4-го порядка включительно ( ). Для этого сформируем 4 расчетные таблицы для
). Для этого сформируем 4 расчетные таблицы для  следующей структуры:
следующей структуры:
| № п/п | 
| 
| 
| 
| 
| 
|

| ||||||

| ||||||
| Сумма |
Заполним таблицу для вычисления  , т.е. при
, т.е. при  :
:
| № п/п | 
| 
| 
| 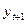
| 
| 
|
| 1,72 | 2,9584 | 3,57 | 12,7449 | 6,1404 | ||
| 3,57 | 12,7449 | 7,45 | 55,5025 | 26,5965 | ||
| 7,45 | 55,5025 | 8,59 | 73,7881 | 63,9955 | ||
| 8,59 | 73,7881 | 9,52 | 90,6304 | 81,7768 | ||
| 9,52 | 90,6304 | 10,66 | 113,6356 | 101,4832 | ||
| 10,66 | 113,6356 | 10,55 | 111,3025 | 112,463 | ||
| 10,55 | 111,3025 | 15,14 | 229,2196 | 159,727 | ||
| 15,14 | 229,2196 | 17,05 | 290,7025 | 258,137 | ||
| 17,05 | 290,7025 | 20,46 | 418,6116 | 348,843 | ||
| 20,46 | 418,6116 | 20,03 | 401,2009 | 409,8138 | ||
| 20,03 | 401,2009 | 27,52 | 757,3504 | 551,2256 | ||
| 27,52 | 757,3504 | 31,72 | 1006,158 | 872,9344 | ||
| 31,72 | 1006,158 | 36,34 | 1320,596 | 1152,705 | ||
| 36,34 | 1320,596 | 42,59 | 1813,908 | 1547,721 | ||
| 42,59 | 1813,908 | 43,51 | 1893,12 | 1853,091 | ||
| Сумма | 262,91 | 6698,31 | 304,7 | 8588,471 | 7546,653 |
Вычислим  по формуле 3.1:
по формуле 3.1:
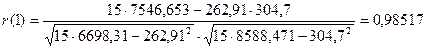 .
.
Далее заполним таблицу для вычисления  , т.е. при
, т.е. при  :
:
| № п/п | 
| 
| 
| 
| 
| 
|
| 1,72 | 2,9584 | 7,45 | 55,5025 | 12,814 | ||
| 3,57 | 12,7449 | 8,59 | 73,7881 | 30,6663 | ||
| 7,45 | 55,5025 | 9,52 | 90,6304 | 70,924 | ||
| 8,59 | 73,7881 | 10,66 | 113,6356 | 91,5694 | ||
| 9,52 | 90,6304 | 10,55 | 111,3025 | 100,436 | ||
| 10,66 | 113,6356 | 15,14 | 229,2196 | 161,3924 | ||
| 10,55 | 111,3025 | 17,05 | 290,7025 | 179,8775 | ||
| 15,14 | 229,2196 | 20,46 | 418,6116 | 309,7644 | ||
| 17,05 | 290,7025 | 20,03 | 401,2009 | 341,5115 | ||
| 20,46 | 418,6116 | 27,52 | 757,3504 | 563,0592 | ||
| 20,03 | 401,2009 | 31,72 | 1006,1584 | 635,3516 | ||
| 27,52 | 757,3504 | 36,34 | 1320,5956 | 1000,0768 | ||
| 31,72 | 1006,1584 | 42,59 | 1813,9081 | 1350,9548 | ||
| 36,34 | 1320,5956 | 43,51 | 1893,1201 | 1581,1534 | ||
| Сумма | 220,32 | 4884,4014 | 301,13 | 8575,7263 | 6429,5513 |
|
|
|
Вычислим  по формуле 3.1:
по формуле 3.1:
 .
.
Выполняя аналогичные вычисления, находим остальные коэффициенты автокорреляции:
 ,
,
 .
.
По итогам вычислений построим таблицу:
| L | r(L) |
| 0,9851704 | |
| 0,9803119 | |
| 0,9705136 | |
| 0,9664745 |
По таблице при помощи Мастера диаграмм строим коррелограмму:

Отсюда следует предположить, что это коррелограмма нестационарного временного ряда с ярко выраженным трендом и отсутствием циклических колебаний.
2. Сформируем расчетную таблицу следующей структуры:
Табл. 3.2
| № п/п | 
| 
| 
| 
| 
| 
| 
| 
|

| ||||||||
| Сумма | ||||||||
| Среднее |
Введем исходные данные  в таблицу и рассчитаем колонки
в таблицу и рассчитаем колонки  ,
,  . Вычисляем суммы и средние значения столбцов с помощью функций СУММ(…) и СРЗНАЧ(…).
. Вычисляем суммы и средние значения столбцов с помощью функций СУММ(…) и СРЗНАЧ(…).
Определяем параметры линейного тренда  по формулам:
по формулам:
 ,
,
 .
.
В итоге получено уравнение тренда:
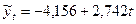 .
.
Вычислим поученные по модели 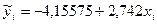 ,
,  значения зависимой переменной
значения зависимой переменной  и заполним колонку
и заполним колонку  расчетной таблицы.
расчетной таблицы.
Далее выполняем расчет величин  и
и  . Из строки «Сумма» столбца
. Из строки «Сумма» столбца  выписываем значение остаточной суммы квадратов
выписываем значение остаточной суммы квадратов
 .
.
По формуле 3.5 находим факторную сумму квадратов:
 .
.
Наблюдаемое значение 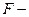 статистики определяем по формуле 3.7:
статистики определяем по формуле 3.7:
 .
.
Табличное значение  =
=  определяем с помощью встроенной статистической функции FРАСПОБР по уровню значимости
определяем с помощью встроенной статистической функции FРАСПОБР по уровню значимости  и числам свободы
и числам свободы 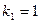 и
и  . Поскольку
. Поскольку  , то можно сделать вывод о статистической значимости построенной модели.
, то можно сделать вывод о статистической значимости построенной модели.
3. Выполним механическое выравнивание по трем ( ) и четырем точкам (
) и четырем точкам ( ) с использованием формулы 3.8. Для этого сформируем расчетную таблицу со следующим титулом:
) с использованием формулы 3.8. Для этого сформируем расчетную таблицу со следующим титулом:
Табл. 3.3
| Исходные данные | Сглаженные данные | ||

| 
| по 3 точкам | по 4 точкам |

| 
| 
|
Заполним колонки  ,
,  таблицы исходными данными.
таблицы исходными данными.
Сглаживание по трем точкам выполним по формуле:
 ,
,
записывая её во второй ячейке колонки  таблицы и с последующей протяжкой результата вычисления до 15 строки.
таблицы и с последующей протяжкой результата вычисления до 15 строки.
При сглаживании по четырем точкам вначале найдем скользящие средние по формуле:
 .
.
Поскольку промежуточных уровней в таблице не предусмотрено, то задаем формулу во второй ячейке колонки  с последующей протяжкой результата вычислений до 14 строки.
с последующей протяжкой результата вычислений до 14 строки.
Затем попарно их центрируем по формуле:
 ,
,
которую задаем в третьей ячейке колонки  , а результат протягиваем до 14 строки. В итоге имеем:
, а результат протягиваем до 14 строки. В итоге имеем:
| Исходные данные | Сглаженные данные | |||
| по 3 точкам | по 4 точкам | |||

| 
| 
| 
| 
|
| 1,72 | ||||
| 3,57 | 4,246666667 | 5,3325 | ||
| 7,45 | 6,536666667 | 7,2825 | 6,3075 | |
| 8,59 | 8,52 | 9,055 | 8,16875 | |
| 9,52 | 9,59 | 9,83 | 9,4425 | |
| 10,66 | 10,24333333 | 11,4675 | 10,64875 | |
| 10,55 | 12,11666667 | 13,35 | 12,40875 | |
| 15,14 | 14,24666667 | 15,8 | 14,575 | |
| 17,05 | 17,55 | 18,17 | 16,985 | |
| 20,46 | 19,18 | 21,265 | 19,7175 | |
| 20,03 | 22,67 | 24,9325 | 23,09875 | |
| 27,52 | 26,42333333 | 28,9025 | 26,9175 | |
| 31,72 | 31,86 | 34,5425 | 31,7225 | |
| 36,34 | 36,88333333 | 38,54 | 36,54125 | |
| 42,59 | 40,81333333 | |||
| 43,51 |
|
|
|
Результаты сглаживания представим в следующих графиках.


Как видно из графиков, сглаживание по 4 точкам оказывается более предпочтительным.
4. Добавим к таблице 3.2 следующие колонки:  .
.
Первые 15 значений колонки  переносим в колонку
переносим в колонку  , начиная с её второй строки с помощью команд: Копирование / Специальная вставка / Значения. Далее по соответствующим формулам заполняются остальные колонки таблицы.
, начиная с её второй строки с помощью команд: Копирование / Специальная вставка / Значения. Далее по соответствующим формулам заполняются остальные колонки таблицы.
| et-1 | et-et-1 | (et-et-1)2 | etet-1 |
| 3,13375 | -0,892 | 0,795664 | 7,02508 |
| 2,24175 | 1,138 | 1,295044 | 7,57655 |
| 3,37975 | -1,602 | 2,566404 | 6,00835 |
| 1,77775 | -1,812 | 3,283344 | -0,06089 |
| -0,03425 | -1,602 | 2,566404 | 0,05604 |
| -1,63625 | -2,852 | 8,133904 | 7,3439 |
| -4,48825 | 1,848 | 3,415104 | 11,8501 |
| -2,64025 | -0,832 | 0,692224 | 9,16761 |
| -3,47225 | 0,668 | 0,446224 | 9,73706 |
| -2,80425 | -3,172 | 10,06158 | 16,7589 |
| -5,97625 | 4,748 | 22,5435 | 7,34033 |
| -1,22825 | 1,458 | 2,125764 | -0,28219 |
| 0,22975 | 1,878 | 3,526884 | 0,48426 |
| 2,10775 | 3,508 | 12,30606 | 11,8366 |
| 5,61575 | -1,822 | 3,319684 | 21,3048 |
| 3,79375 | -3,7938 | 14,39254 | -8,8E-14 |
| Сумма | -3,1338 | 91,47034 | 116,146 |
Отметим, что первые строки всех добавленных колонок, начиная с колонки  , будут пустыми. В строке «Сумма» находим необходимые данные:
, будут пустыми. В строке «Сумма» находим необходимые данные:
 ,
,
и по формуле 3.9 находим значение критерия Дарбина-Уотсона:
 .
.
С использованием формулы 3.10 определяем выборочное значение коэффициента автокорреляции:
 .
.
По значениям  0,05,
0,05,  16,
16,  1 из таблицы теста Дарбина-Уотсона находим критические точки:
1 из таблицы теста Дарбина-Уотсона находим критические точки:  . Поскольку
. Поскольку  , то по правилу 3.11 устанавливаем наличие положительной автокорреляции и в остатках. При этом выборочный коэффициент автокорреляции в остатках составляет величину
, то по правилу 3.11 устанавливаем наличие положительной автокорреляции и в остатках. При этом выборочный коэффициент автокорреляции в остатках составляет величину  .
.
|
|
|