Преломление света в линзах

ОПТИКА

В этом разделе изучаются законы излучения, поглощения и распространения света. Свет имеет двойственную природу: он проявляет себя и как поток частиц - фотонов (квантов света), и как. электромагнитное излучение (электромагнитная волна). Это свойство называется корпускулярно - волновым дуализмом света. В одних явлениях более выражены волновые свойства света (интерференция, дифракция, поляризация), в других – корпускулярные (фотоэффект, тепловое излучение, эффект Комптона). Ряд оптических явлений к настоящему времени удалось объяснить и с волновых, и с корпускулярных (квантовых) позиций.

ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА

Из­вестно, что в оп­тически однород­ной среде свет рас­простра­няется прямолинейно с постоянной скоростью v. Величина

 

n = с/ v (1.1)

 

называется абсолютным показателем преломления среды.

Здесь с = 3∙10⁸ м/с - скорость света в вакууме.

При падении света на границу раздела двух сред происходит отражение и преломление луча (рис.1). Угол падения светового луча равен углу отражения, т. е.

α = α′. (1.2)

 

Это условие называют законом отражения.

Луч падающий, отраженный и преломленный, а также перпендикуляр, проведенный в точку падения, лежат в одной плоскости. Причем

 

(1.3)

где n₁ и n₂ - абсолютные показатели преломления первой и второй сред; n_{21 -} относительный показатель преломления второй среды относительно первой; β - угол преломления светового луча.

Последнее выражение является законом преломления света.

Как видно из (1.3), при падении света из среды, оптически менее плотной, в среду с большей оптической плотностью (n₁ ‹ n₂ ) угол преломления β меньше угла падения α. В обратном случае (при n₁ › n₂) угол β больше угла α (рис. 2), и возможна такая ситуация, при которой преломленный луч скользит вдоль границы раздела сред (рис. 2, пунктир), т. е β = 90 º.

Угол падения, соответствующий этому случаю называется предельным (α_пр). При падении света под углом большим предельного преломленный луч во вторую среду вообще не выходит, а, отражаясь от границы раздела, возвращается в первую среду. Это явление носит название полного внутреннего отражения.

 

ПРИМЕР. На плоскопараллельную стеклянную пластинку с показателем преломления 1,5 и толщиной d = 5 см падает луч лазера под углом α = 30º и выходит параллельно первоначальному лучу. Определить расстояние l между вышедшими лучами.

 

РЕШЕНИЕ. Ход лучей в пластинке изображен на рис. 3. Используя закон преломления света, найдем угол β:

 

 

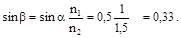
Отсюда следует, что угол β = 19º30′.

Расстояние l между лучами можно найти из ∆ BED:

l = BD∙cos α.

 

Отрезок BD определим, рассмотрев ∆ BСD:

 

BD = 2ВК = 2d tg β.

 

Тогда

l = 2d∙tg β∙cos α =2d∙tg 19º30′ ∙cos 30º = 2∙5∙0, 3541∙0,8665 = 0,3063 (см).

 

ПРЕЛОМЛЕНИЕ СВЕТА В ЛИНЗАХ

 

Линзами называются объекты из прозрачных материалов, ограниченные с двух сторон преломляющими поверхностями, чаще всего сферическими. Линзы бывают двояковыпуклыми, двояковогнутыми, плосковыпуклыми, плосковогнутыми и т.д. При этом плоскую поверхность можно рассматривать как сферическую бесконечно большого радиуса кривизны.

Фокусом линзы называется точка, в которой после преломления линзой пересекаются лучи, падающие на линзу параллельно ее оптической оси. Расстояние F от фокуса до центра линзы называется фокусным расстоянием линзы.

Для тонкой линзы, помещенной в однородную среду, выполняется соотношение

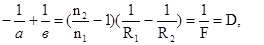(1.4)

 

где а и в - соответственно расстояния от линзы до объекта и от линзы до изображения; R₁ и R₂ - радиусы кривизны ограничивающих поверхностей; F - фокусное расстояние линзы; D = 1/F - оптическая сила линзы(в системе СИ измеряется в диоптриях, дптр). Все расстояния, отсчитываемые по ходу луча, берутся со знаком “+” против хода луча - со знаком “-”.

Увеличением линзы k называется отношение размера изображения к размеру объекта.

 

ПРИМЕР. На расстоянии а = 25 см от двояковыпуклой линзы Л оптической силой D = 10 дптр поставлен предмет высотой АВ= 3 см. Найти положение и высоту изображения предмета А₁В₁, а также увеличение линзы k.

 

РЕШЕНИЕ. Определим фокусное расстояние линзы

 

F = 1/ D = 1/10 =0,1 (м).

 

Построим изображение объекта АВ. Для этого от каждой из точек А и В нужно провести не менее двух лучей. Проведем лучи АВ₁ и ВА₁ через центр линзы; при этом они не изменяют своего направления. Еще два луча, идущие от точек А и В параллельно оптической оси, проходят через фокус линзы F. В результате построения видим, что полученное изображение является действительным, обратным и уменьшенным.

По формуле (1.4) найдем расстояние в от линзы до изображения:

 

Из подобия треугольников АОВ и А₁ОВ₁ следует, что

 

А₁В₁ = АВ ∙ в / а = 3∙0,16/0,25 = 1,82 (см)

 

Увеличение линзы k = А₁В₁ /АВ = 1,82/3 = 0,66.

 

ИНТЕРФЕРЕНЦИЯ СВЕТА

 

При сложении двух когерентных волн интенсивностей I ₁ и I ₂ интенсивность I результирующей волны равна

____

I = I ₁ + I ₂ + 2√ I ₁ I ₂ соs δ, (1.5)

 

где δ - разность фаз складывающихся волн.

В тех точках пространства, где соs δ › 0, результирующая интенсивность больше суммы интенсивностей исходных волн,т.е. I › I ₁ + I ₂. А там, где соs δ ‹ 0, наоборот - результирующая интенсивность меньше суммы интенсивностей исходных волн - I ‹ I ₁ + I ₂.

Следовательно, происходит перераспределение энергии светового потока: в одних местах волны усиливают друг друга, там наблюдаются максимумы интенсивности света, а в других волны ослабляют друг друга и там имеют место минимумы интенсивности света. Это явление называется интерференцией света.

Оптический путь L световой волны - это произведение геометрической длины пути s световой на показатель преломления среды n:

 

L = s n. (1.6)

 

Оптической разностью хода двух световых волн называется величина

 

Δ = L ₂ - L ₁ = s ₂ n ₂ - s ₁ n ₁. (1.7)

Оптическая разностью хода волн Δ связана с их разностью фаз δ соотношением

δ

Δ = –– λ₀. (1.8)

2π

 

Здесь λ₀ - длина волны в вакууме.

Если оптическая разность хода волн равняется четному числу полуволн, т.е.

Δ = ± 2 m λ₀/2 = ± m λ₀, (1.9)

 

то при их наложении наблюдается интерференционный максимум. Если же оптическая разность хода волн равняется нечетному числу полуволн

 

Δ = ± (2 m + 1) λ₀/2, (1.10)

 

то при их сложении имеет место минимум интерференции.

Расстояние между соседними максимумами (или минимумами) называется шириной интерференционной полосы Δ х. При наблюдении интерференционной картины от двух когерентных источников света (опыт Юнга, зеркала Френеля, бипризма Френеля и т.д.) ширина интерференционной полосы рассчитывается по формуле

l

Δ х = ––– λ, (1.11)

d

 

где l – расстояние от источников света до экрана наблюдения; d – расстояние между источниками света; λ - длина волны.

Оптическая разность хода световых волн при отражении от тонкой пленки

_________

Δ = 2 d√ n ² - sin² α ± λ/2 = 2 d n cos β ± λ/2. (1.12)

 

Здесь d – толщина пленки; α и β – углы падения и преломления волны. Дополнительная разность хода ± λ/2 возникает из-за потери полуволны при отражении света от среды, оптически более плотной.

Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)

(1.13)

 

Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем)

(1.14)

 

где R – радиус линзы; m – номер кольца; n – показатель преломления среды, находящейся между линзой и стеклянной пластинкой.

 

ПРИМЕР. На плоскопараллельную пленку с показателем преломления 1,25, находящуюся в воздухе, нормально падает параллельный пучок монохроматического света длины волны λ. Как будет выглядеть эта пленка в отраженном свете, если ее толщина d = 10 λ?

 

РЕШЕНИЕ. Рассмотрим луч света 1, принадлежащий падающему световому пучку. Известно, что при нормальном падении преломленный луч не меняет своего направления. В точке А луч света 1 частично отражается от первой грани пленки в обратном направлении (луч 1΄), частично проходит в первоначальном направлении до точки В и отражается от второй грани пленки (1΄΄). Для удобства лучи 1΄ и 1΄΄ изображены раздельно, на самом деле они идут по одному направлению. Лучи 1΄ и 1΄΄ являются когерентными, т.к. получены делением одного луча на два, и могут интерферировать при наложении. Поскольку потеря полуволны происходит при отражении света от верхней границы пленки, оптическая разность хода лучей в данном случае определится как

 

Δ = L ₂ - L ₁ = 2 d n - (- λ/2) = 2 d n + λ/2. (1.15)

Так как толщина пленки и угол падения лучей не меняется, то разность хода интерферирующих лучей по всей пленке одинакова. Поэтому пленка будет окрашена равномерно: при выполнении условия интерференционных минимумов (1.10) она будут темной, а при выполнении условия максимумов (1.9) она будет окрашена в цвет падающего монохроматического излучения.

В общем виде можно записать

 

2 d n + λ/2 = х λ/2, (1.16)

 

имея в виду, что при четном х пленка в отраженном свете будет светлой, а при нечетном - темной.

Найдем величину из равенства (1.16):

 

2 d n + λ/2 4 d n

х = –––––––––-- = ––––- +1;

λ/2 λ

 

4∙10∙λ∙1,25

х = –––––––––-- + 1 = 51,

λ

 

т.е. получили нечетное число, откуда следует, что пленка в отраженном свете будет темной.

 

ПРИМЕР. Явление интерференции света применяется для определения показателей преломления прозрачных материалов с помощью приборов, называющихся интерференционными рефрактометрами. На рис.6 приведена принципиальная схема такого рефрактометра. Здесь S - узкая щель, через которую проходит свет длины волны λ = 589 нм; 1 и 2 – кюветы длиной l = 10 см каждая, заполненные воздухом показатель преломления которого n = 1,000277; L₁ и L₂ - линзы; Э – экран для наблюдения интерференционной картины. При замене в одной из кювет воздуха на аммиак интерференционная картина на экране сместилась на N = 17 полос относительно первоначальной картины. Определить показатель преломления аммиака.

 

РЕШЕНИЕ. Рассмотрим точку А в центре экрана Э. Очевидно, что оптическая разность хода лучей Δ₁ в случае заполнения обеих кювет воздухом, равняется нулю. Из условия максимумов Δ₁ = m ₁λ = 0 следует, что и порядок максимума m ₁ в точке А тоже равен нулю.

При заполнении одной из кювет аммиаком оптическая разность хода лучей Δ₂ в этой точке составит

 

Δ₂ = n_а l - n l = m ₂λ, (1.17)

 

где m ₂ – новый порядок максимума, который по условию задачи равняется m ₂ = m ₁ + N. Из-за этого интерференционная картина и во всех точках экрана сместилась на N полос. Отсюда следует

 

n_а l - n l = m ₂λ = (m ₁ + N) λ;

 

m ₁ + N

n_а = n + ––––––– λ;

l

0 + 17

n_а = n + 1,000277 + ––––––– ∙589∙10^-9 = 1, 001278.

10^-2

Следует обратить внимание на высокую точность измерения показателя преломления таким методом.

 

ДИФРАКЦИЯ СВЕТА

Дифракция света – это огибание волнами препятствий по размерам сравнимых с длиной волны излучения, вследствие чего волны отклоняются от своего прямолинейного распространения. Это явление имеет место для волн любой природы - механических, электромагнитных и т. д.

Радиусы зон Френеля для сферических волн

 

(1.18)

для плоских волн

 

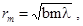(1.19)

 

где а и b – расстояния от источника волны до препятствия и от препятствия до точки наблюдения соответственно; m – номер зоны; λ - длина волны.

При дифракции плоской световой волны на прямоугольной бесконечно длинной щели шириной а условие дифракционных максимумов

 

(1.20)

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: