 |
Пример составления уравнений движения машины
|
|
|
|
Пример выполнения задания типового расчёта
По динамике машины с кулисным приводом
Постановка задачи
Изложим, следуя [4], постановку задания типового расчёта по динамике машины с кулисным приводом.
Требуется определить движение машины с кулисным приводом под действием заданных сил и моментов, а также найти динамические реакции. Числовые значения параметров и начальные условия подобраны так, чтобы движение было близко к периодическому.
Машина приводится в движение электродвигателем, развивающим момент; для проекции на ось пользуемся таким выражением:
, (58)
где – пусковой момент, – крутизна статической характеристики, – номер звена, к которому приложен момент.
В разных вариантах задания полезную нагрузку моделируют либо сила нагрузки, либо момент нагрузки, задаваемые так:
или,; (59)
здесь в роли точки может выступать либо произвольная точка звена 4 (если оно движется поступательно), либо центр масс данного звена (если для него имеет место общий случай плоского движения), а в роли коэффициентов, выступают коэффициенты сопротивления.
Во всех вариантах звено 1 – это маховик, звено 2 – кулиса, в прорези которой движется шип маховика. Элементы конструкции машин считаются абсолютно жёсткими, ремни – нерастяжимыми и безынерционными. Проскальзывание колёс, ремней и т.д. отсутствует. Трением между шипом и прорезью кулисы пренебрегаем.
Исходные значения параметров приведены в табл.1. Значения четырёх из этих параметров следует модифицировать по формулам
;;
;;
здесь – номер студенческой группы, – номер потока.
Во всех вариантах,. В вариантах 7, 9, 11, 24 для звена 4 радиус инерции.
|
|
|
Время моделирования и начальная угловая скорость маховика задаются так:
; (61)
(при этом будет близко к среднему значению в периодическом движении, а – близко ко времени полного оборота маховика).
Варианты схем машин представлены на рис.10–14.
Таблица 1
| ант | ||||||||||||||
| 0,8 | 1,4 | 9,26 | 0,18 | 1,6 | ||||||||||
| 3,3 | 2,0 | 0,13 | ||||||||||||
| 0,3 | 9,56 | 1,5 | 7,72 | 0,12 | 0,12 | 3,1 | ||||||||
| 0,2 | 3,48 | 1,7 | 4,63 | 0,09 | 0,09 | 1,6 | ||||||||
| 3,5 | 2,0 | 0,12 | 0,08 | 0,09 | 1,5 | |||||||||
| 0,8 | 4,72 | 1,4 | 9,26 | 0,18 | 0,10 | 3,2 | ||||||||
| 0,2 | 20,6 | 1,5 | 7,72 | 0,09 | 0,1 | 0,12 | 0,08 | 1,6 | ||||||
| 3,5 | 2,0 | 0,10 | 0,08 | 0,09 | 3,1 | |||||||||
| 0,2 | 20,6 | 1,4 | 9,26 | 0,09 | 0,13 | 0,15 | 0,05 | |||||||
| 3,8 | 2,0 | 0,18 | 0,08 | 0,12 | 3,1 | |||||||||
| 0,4 | 11,5 | 1,7 | 4,63 | 0,12 | 0,08 | 0,12 | 0,06 | 4,7 | ||||||
| 3,7 | 2,0 | 0,16 | 0,12 | 0,14 | ||||||||||
| 3,7 | 2,0 | 0,12 | 3,1 | |||||||||||
| 3,8 | 2,0 | 0,10 | 0,06 | 0,08 | 4,7 | |||||||||
| 3,9 | 2,0 | 0,20 | 0,06 | 0,14 | 3,2 | |||||||||
| 3,9 | 2,0 | 0,10 | 0,05 | 0,08 | ||||||||||
| 0,4 | 6,95 | 1,4 | 9,26 | 0,12 | 0,12 | |||||||||
| 3,9 | 2,0 | 0,08 | 3,1 | |||||||||||
| 3,9 | 2,0 | 0,14 | 0,07 | 0,08 | ||||||||||
| 4,0 | 3,24 | 2,0 | 0,10 | 3,1 | ||||||||||
| 4,0 | 2,0 | 0,07 | 3,2 | |||||||||||
| 4,1 | 2,0 | 0,18 | 0,06 | 0,12 | ||||||||||
| 0,4 | 6,10 | 1,5 | 7,72 | 0,12 | 0,10 | 1,5 | ||||||||
| 0,2 | 49,2 | 1,7 | 4,63 | 0,09 | 0,11 | 0,16 | 0,08 | 3,1 | ||||||
| 1,0 | 35,4 | 1,4 | 9,26 | 0,18 | 0,14 | 1,6 | ||||||||
| 4,2 | 2,0 | 0,18 | 0,09 | 0,10 | ||||||||||
| 0,4 | 29,9 | 1,5 | 7,72 | 0,12 | 0,16 | |||||||||
| 4,3 | 2,0 | 0,15 | 3,1 | |||||||||||
| 4,2 | 2,0 | 0,05 | 3,2 | |||||||||||
| 1,0 | 5,36 | 1,4 | 9,26 | 0,18 | 0,10 |
|
|
|

| 
| ||

| 
| ||

| 
|
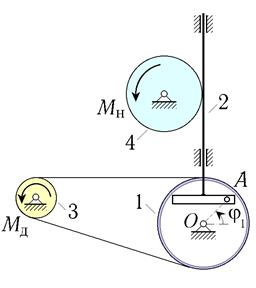
Рис. 10. Схемы машин с кулисным приводом (варианты 1–6)

| 
| ||

| 
| ||

| 
|
Рис. 11. Схемы машин с кулисным приводом (варианты 7–12)

| 
| ||

| 
| ||

| 
|
Рис. 12. Схемы машин с кулисным приводом (варианты 13–18)

| 
| ||

| 
| ||

| 
|
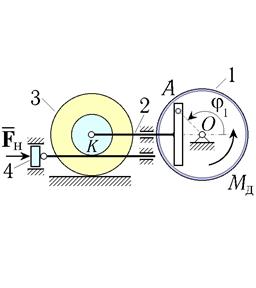
Рис. 13. Схемы машин с кулисным приводом (варианты 19–24)

| 
| ||
| 
| ||

| 
|
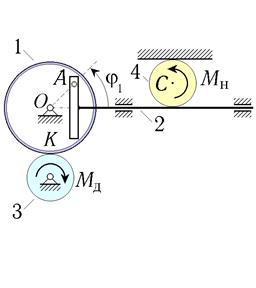
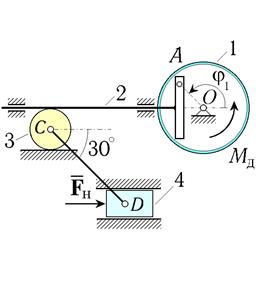
Рис. 14. Схемы машин с кулисным приводом (варианты 25–30)
: Выполнить компьютерное моделирование движения машины (отдельные этапы моделирования рассматриваются далее – применительно к конкретному примеру). Для момента времени, когда угловое ускорение принимает максимальное по модулю значение, определить динамические реакции: а)окружное усилие в точке (варианты 1, 2, 3, 5, 6, 7, 8, 10, 12, 13, 14, 15, 19, 20, 22, 23, 24, 26, 27, 29); б)разность сил натяжения ведущей и ведомой ветвей ременной передачи (варианты 4, 9, 11, 17, 25, 30); в)усилие в стержне (варианты 16, 18, 21, 28).
В заданиях данного ТР уравнения движения машины составляются в форме уравнений Лагранжа 2-гo рода. За обобщённую координату принимаем угол (рассматриваемые механические системы имеют одну степень свободы), так что при переходе к записи в форме Коши (1) получим:
,,. (62)
Эти дифференциальные уравнения и интегрируются численно на интервале изменения времени,. Если задача решена правильно, то графики, и не будут иметь разрывов, конечные значения переменных и будут близки к начальным, а приращение угла на интервале изменения времени, будет близко к.
Что касается определения динамических реакций, то для нахождения соответствующей реакции рекомендуется освободить от связей одно из звеньев системы, а затем составить такое из уравнений динамики данного звена, в которое вошла бы искомая реакция. В данное уравнение вместо переменных, и надо подставить их значения из той строки таблицы результатов моделирования, в которой принимает максимальное по модулю значение.
|
|
|
Пример составления уравнений движения машины
Рассмотрим один из вариантов задания типового расчёта по динамике машины с кулисным приводом (условимся считать его 31-м вариантом). Пусть,, а кинематическая схема машины соответствует изображённой на рис.15, а.
В данном варианте момент двигателя приложен к шкиву 3, связанному с маховиком ременной передачей. Полезная нагрузка моделируется силой, приложенной к точке штока 5.
:;;;;;;;;;;;;;;;.
Предполагается, что ремень невесомый, нерастяжимый, не проскальзывающий относительно шкива и маховика. Каток 4 относительно рейки штока 5 и неподвижной рейки не проскальзывает (зубчатая реечная передача). Масса штока не учитывается.

|
Рис. 15. Схема машины с кулисным приводом (вариант 31)
: Составить уравнения движения машины в форме уравнений Лагранжа 2-го рода. Записать уравнения движения в форме Коши. При заданных начальных условиях численно проинтегрировать уравнения движения на отрезке,. Построить графики,,. Для момента времени, когда принимает максимальное по модулю значение, вычислить разность сил натяжения ведущей и ведомой ветвей ременной передачи.
Приступаем к составлению уравнений движения машины. Будем придерживаться той последовательности действий, которая изложена в п.4 раздела 1.
1.Составим выражение для кинетической энергии механической системы, указав вид движения каждого тела и выразив коэффициенты через исходные данные.
.
Здесь мы учли, что маховик 1 и шкив 3 совершают вращательное движение вокруг неподвижных осей, кулиса 2 движется поступательно, а для ступенчатого катка 4 имеет место общий случай плоского движения, после чего воспользовались формулами (15) (кинетическая же энергия безынерционного штока 5 равна нулю). При вычислении моментов инерции было учтено, что шкив 3 – однородный диск, для маховика 1 момент инерции задан, а для ступенчатого катка 4 известен радиус инерции.
|
|
|
2.Составим выражение для обобщённой силы и раскроем скалярные произведения.
Воспользуемся формулой (17) и заметим, что в нашей задаче к числу активных сил и моментов относятся момент, сила и силы тяжести.
,,,
,,,
.
В проделанных выкладках мы учли следующее. Векторы скоростей неподвижных точек и равны нулю (соответствующие же передаточные функции отличаются от скоростей лишь скалярным множителем и, значит, тоже равны нулю). Вместо и мы подставили конкретные выражения из (58),(59).
Подчеркнём, что к концу данного пункта в наших формулах уже больше не должны фигурировать обозначения и.
Поскольку кулиса 2 движется поступательно, то все её точки имеют одинаковые скорости; поэтому вместо передаточной функции линейной скорости центра масс кулисы (где приложена сила тяжести) мы воспользовались передаточной функцией линейной скорости точки.
Раскрывая скалярные произведения, мы учли, что векторы и направлены параллельно оси (так что их проекции на ось равны нулю).
3.Выберем обобщённую координату и выясним кинематический смысл:
Выбор обобщённой координаты в данной задаче был предписан условием задачи. Поскольку – это угол поворота маховика 1, то производная от этой обобщённой координаты равна проекции угловой скорости маховика на ось.
Теперь надо выразить все линейные и угловые скорости, входящие в формулы из пунктов 1 и 2 нашего алгоритма, через обобщённую скорость. Заметим, что эти скорости либо непосредственно входят в данные формулы, либо представлены передаточными функциями.
4.Выразим линейные и угловые скорости, входящие в выражения для и, через.
Первое нужное нам выражение сразу же следует из результатов пункта 3:
.
Кинематический граф
позволяет записать соотношение
,
откуда, учитывая, что, получаем:
.
Так как кулиса 2 движется поступательно и её перемещение вдоль оси равно перемещению точки вдоль этой оси, то
,.
Заметим, что перемещение точки вдоль оси никак не сказывается на движении кулисы, точки которой движутся только вдоль оси. Поэтому было бы грубой ошибкой записать, что.
После этого из графа
OB → D H
найдём:
,
откуда
,.
Для нахождения угловой скорости ступенчатого катка 4 воспользуемся тем, что его точка – это точка контакта с неподвижной стенкой, причём качение происходит без проскальзывания; поэтому.
Граф
C K
даёт:
,
откуда
. (8)
,.
|
|
|


