Полотняного плетения с поликристаллической матрицей

КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СЛОЕ ТКАНОГО КОМПОЗИТА

 

Дедков Д. В., Зайцев А. В., Ташкинов А. А.

Пермь, Россия

 

Тканые композиты с поликристаллической матрицей получили широкое распространение в авиационной и космической промышленности. Из таких материалов изготавливают несущие панели крыла, оперения и фюзеляжа самолетов, лопатки турбин, сопловые блоки, носовые обтекатели ракетных двигателей, уплотнительные элементы для трубопроводов гидро и пневмосистем и многие другие элементы конструкций, эксплуатируемые в условиях интенсивного теплового (или криогенного) и механического воздействия [1]. Отличительной особенностью процесса изготовления готовых изделий из этих материалов является раскрой и выкладка на оправку слоев ткани с искривленными волокнами (полотняной, сатиновой, саржевой и др.), а также прошивка этих слоев между собой. Полученный армирующий каркас насыщается поликристаллической матрицей, в результате чего происходит одновременное создание самого элемента конструкции и материала, из которого он изготовлен.

При производстве изделий из тканых композитов неизбежны технологические дефекты, снижающие эксплуатационные свойства изделий. К числу типичных дефектов относятся отсутствие (пропуск) волокон основы или утка, разрывы волокон при прошивке слоев, а также внутренние поры, которые обнаруживаются только на этапе выходного ультразвукового контроля. Гарантированное обеспечение наличия в этих участках поликристаллической матрицы (при осаждении из газовой фазы или при карбонизации полимеров после пропитки под давлением, вакуумирования и доуплотнения армирующего каркаса), матрицы на основе терморасширенного графита (после прокатки слоев фольги) или керамики затруднено [2]. Это связано с тем, что образующиеся на поверхности нитей слой осаждаемого материала препятствует дальнейшему насыщению каркаса.

Применение тканых композитов для изготовления элементов конструкций ответственного назначения, работающих в условиях многократно изменяющихся внешних нагрузок в течении длительного срока эксплуатации, предопределяет необходимость прогнозирования не только эффективных деформационных характеристик, но и проведения уточненного прочностного анализа. Это, в свою очередь, актуализирует построение математических моделей поведения слоев этих материалов с локальными дефектами при комбинированных многоосных квазистатических нагружениях.

В настоящей работе решена более частная задача по определению коэффициентов концентрации напряжений в слое композита полотняного плетения (саржа 1/1 с равными рапортами по основе и утку), вызванных сложной геометрией переплетения волокон и наличием локальных технологических дефектов (внутренними порами и локальными разрывами волокон), а также выявлению механизмов, определяющих сценарии начального разрушения, с использованием разработанной ранее двухуровневой модель тканого материала с искривленными волокнами и поликристаллической матрицей [3, 4, 5]. Выбор полотняного переплетения обеспечивает с одной стороны наиболее короткие перекрытия нитей, наибольшую прочность, плотность и повышенную жесткость, однородную, геометрически идентичную с лицевой и изнаночной стороны поверхность ткани, с другой — наличие внутренних технологических пор.

Рассмотрим слой тканого композита, толщиной , с армирующим каркасом полотняного переплетения, образованного волокнами круглого поперечного сечения с постоянным диаметром . Следуя [6], искривление волокон основы и утка ткани будем задавать дугой окружности с центральным углом и участком прямой.

В тканых композитах армирующий каркас несет силовую нагрузку, а матрица служит для перераспределения напряжений между нитями. В процессе изготовления композита не удается исключить их соприкосновение. Поэтому будем предполагать, что искривленные волокна, принадлежащие слоям идеальной периодической структурой, не всегда окружены гарантированным слоем поликристаллической матрицы и содержат локальные замкнутые технологические поры. Кроме того, в силу малости деформаций будем считать углы неизменными при нагружении слоя.

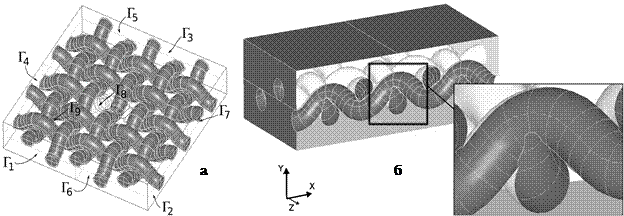
Для построения геометрической модели будем использовать препроцессор, входящий в состав платформы SALOME-MECA [7]. Этот пакет был разработан и сертифицирован для французской энергетической отрасли и предназначен для решения задач механики сплошных сред, термо- и гидродинамики, акустики и магнетизма, выполнения расчетов для строительных конструкций и сооружений. На рис. 1 представлены фрагменты слоя тканого композита с коэффициентами армирования . Здесь и далее оси и ортогональной декартовой системы координат будут принадлежать плоскости слоя.

Рис 1. Фрагменты слоя тканого композита полотняного плетения

с технологическими дефектами: локальный разрыв нити утка (а),

внутренняя технологическая пора (б)

Будем рассматривать наиболее типичные дефекты (которые являются локальными концентраторами напряжений): полости, связанные со случайными разрывами утка (рис. 1, а) или основы и утка, образующиеся в результате сшивки слоев или имеющимися в исходной ткани до прошивки, а также внутренние поры (рис. 1, б), расположенные в областях вблизи участков наибольшего искривления волокон, в результате недостаточного насыщения материалом матрицы, вызванные короткими перекрытиями и соприкосновениями нитей армирующего каркаса. Размеры образующихся в результате полостей соизмеримы с характерными размерами неоднородностей, не изменяют значительно интегральные коэффициенты армирования композита, могут оказаться частично или полностью заполненными материалом матрицы.

Для простоты предположим, что волокна и матрица слоя модельного тканого композита изотропные, линейно упругие, не изменяющие геометрию, взаимное расположение и тип симметрии при нагружении. Тогда компоненты тензора напряжений удовлетворяют уравнения равновесия, а компоненты тензора малых деформаций связаны с компонентами вектора перемещений геометрическими соотношениями Коши

, . (1)

Для описания геометрии слоя тканого композита введем единичную, кусочно-однородную индикаторную функцию радиус-вектора , которая принимает значение 1, если точка принадлежит волокну основы или утка и 0, если матрице. Тогда определяющие соотношения запишем следующим образом:

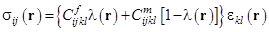, (2)

где верхними индексами и отмечены материальные коэффициенты, относящиеся к нитям армирующего каркаса и матрице соответственно.

Дополним краевую задачу (1) – (2) граничными условиями:

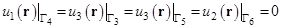, , , (3)

,

,

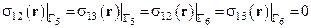обеспечивающими заданное макрооднородное неравнокомпонентное деформирование в плоскости слоя. Условия идеального сопряжения

, , (4)

на границах раздела фаз 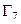(рис. 1, а) описывают совместную работу нитей и поликристаллической матрицы при нагружении. Будет предполагать, что на этих границах также отсутствуют химические реакции и фазовые переходы в процессе нагружения слоя.

В случае, если в модельном материале не исключается возможность контакта волокон основы и утка, на соответствующих поверхностях (положение и геометрия которых считаются заданными и неизменными в процессе нагружения слоя) будем считать справедливыми условия контакта с кулоновским трением: если , то

, , (5)

а, если , то

, . (6)

Здесь — статический коэффициент трения, а индексы и определяют направление внешней нормали и касательной к поверхности .

Внутренняя пора (рис. 1, б) моделируется исключением из рассмотрения локального объема матрицы. Точки образовавшейся внутренней поверхности не имеют ограничений на перемещения, а сама поверхность свободна от напряжений:

. (7)

Численное решение краевой задачи (1) – (3) с граничными условиями (4) – (7) проводилось методом конечных элементов, с помощью некоммерческого пакета Code-Aster, входящего в состав платформы SALOME-MECA [7]. Степень дискретизации фрагментов проводилась на 16-узловые тетраэдральные и 20-узловые гексаэдральные изопараметрические элементы выбиралась таким образом, чтобы полученные в результате численного решения поля структурных перемещений, деформаций и напряжений в слое тканого композита без локальных дефектов и с несовершенствами ни качественно, ни количественно не изменялись при уменьшении характерных размеров конечных элементов. Этим условиям удовлетворяют конечно-элементные сетки (рис. 2), параметры которых представлены в табл. 1.

В качестве примера рассмотрим результаты макроскопически однородного чистого формоизменения слоя тканого композита с поликристаллической матрицей. В этом частном случае на границах и должны быть заданы перемещения , . Модуль Юнга и коэффициент Пуассона материала нитей армирующего каркаса соответствовали работе [8] и принимали значения: ГПа и . Упругие модули поликристаллической матрицы были выбраны следующим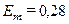и: ГПа и . Статический коэффициент трения соответствовал скольжению керамического волокна по поверхности поликристаллической матрицы.

Рис 2. Дискретизация матрицы и волокон армирующего каркаса

слоя тканого композита полотняного плетения

Таблица 1.

Параметры конечно-элементной сетки

Слой композита с иде­альной периодической структурой	Нити с гарантированным слоем матрицы	298 255 / 77 760
Нити имеют поверхность контакта с трением	405 480 / 77 760
Разрыв нитей утка	Нити с гарантированным слоем матрицы	285 466 / 75 168
Нити имеют поверхность контакта с трением	405 480 / 75 168
Разрыв нитей основы и утка	Нити с гарантированным слоем матрицы	279 276 / 72 576
Нити имеют поверхность контакта с трением	405 480 / 72 576

Примечание: 16-узловые тетраэдральные элементы (числитель), 20-узловые гексаэдраль­ные (знаменатель)

В табл. 2 представлены безразмерные коэффициенты 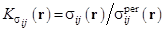, определяемые отношением компонент тензора напряжений в геометрическом центре межволоконного пространства модельной структуры с локальным дефектом к соответствующим компонентам тензора напряжений в идеальной периодической структуры, в той же точке. Выбор точек, в которых определяются значения коэффициентов концентрации напряжений, обусловлен необходимостью исключения областей сингулярности поля напряжений, которые имеют место вблизи границ технологических дефектов.

Таблица 2.

Максимальные коэффициенты концентрации напряжений в слое тканого композита

Локальный технологический дефект
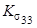
Разрыв нити основы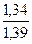
Разрыв нити основы с последующим дополнительным насыщением поры
Разрыв нитей основы и утка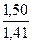
Разрыв нитей основы и утка с последующим дополнительным насыщением поры

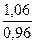
Примечание: каждая нить армирующего каркаса окружена гарантированным слоем матри­цы (числитель), имеют общую поверхность контакта с трением, а между участками с наибольшей кривизной располагаются внутренние поры (знаменатель)

Рис. 3. Распределение коэффициентов концентрации интенсивности напряжений

в фрагменте тканого композита с локальным разрывом нити утка

На рис. 3 показано распределение коэффициентов концентрации интенсивностей напряжений в нитях, а в табл. 2 представлены максимальные значения в матрице слоя тканого композита в геометрическом центре межволоконного пространства, вблизи локального дефекта (разрыв искривленных волокон основы и/или утка). Области поликристаллической матрицы, в которых анализировалось напряженное состояние, были выбраны таким образом, чтобы исключить точки сингулярности поля напряжений, которые могут возникать на границах полостей технологических дефектов.

Коэффициенты концентрации интенсивностей напряжений достигают максимальных значений в местах наибольшего искривления нитей и располагаются строго периодично. Исключение составляют области вблизи локального дефекта, где исследуемый параметр достигает значений 1,6 и 2,5 для случаев, когда армирующие элементы окружены гарантированной прослойкой матрицы и имеют контакт с трением соответственно.

В случае разрыва нитей основы и/или утка при условии, что каждое волокно композита окружено гарантированным слоем матрицы, наибольший вклад в коэффициенты концентрации напряжений вносят нормальная составляющая . Полученные результаты (табл. 2) свидетельствуют о том, что при макроскопически однородном чистом формоизменении фрагмента тканого композита разрушение матрицы в рассматриваемой точке может быть инициировано по механизмам отрыва в направлении утка.

При наличии контакта с трением между искривленными волокнами тканого композита увеличиваются в 1,4–2,7 раз коэффициенты концентрации напряжений (табл. 2). Это связано с тем, что в рассматриваемом случае в слое армированного материала кроме концентраторов, вызванных контактом с трением, появляются внутренние замкнутые области в местах наибольшего искривления переплетенных нитей, не содержащие материала связующего.

Дополнительное насыщение полости, возникающей на месте разрыва утка и основы, не приводит к смене механизма возможного разрушения слоя: как и прежде, начало потери несущей способности будет вызвано отрывом в направлении утка. Насыщение материалом матрицы полости, возникающей на месте разорванной нити основы, приводит локальному изменению (на масштабах, соизмеримых с характерным размером волокон) симметрии армирующего каркаса и, как следствие — смене механизма разрушения (об этом свидетельствует превышающее в 1,85–2,34 раз значение коэффициента ). В рассматриваемом случае доминирующими механизмами начала разрушения являются разрыв матрицы в направлении, перпендикулярном плоскости слоя.

Полученные результаты позволяют сделать вывод о том, что для повышения способности тканым композитом сопротивляться внешнему воздействию необходимо предусмотреть в технологическом процессе операции, обеспечивающие проникновение связующего в полости технологических локальных дефектов (дополнительная пропитка, доуплотнение и карбонизация, доосаждение поликристаллической матрицы из газовой фазы) в случае, если обнаруживаются закрытые внутренние поры. В противном случае возможно разрушение материала матрицы по механизмам сдвига и отрыва.

Работа выполнена в рамках задания № 2014/152 на выполнение государственных работ в сфере научной деятельности в рамках базовой части госзадания Минобрнауки РФ (код проекта — 1911).

 

Литература

1. И.В. Буланов, В.В. Воробей. Технология ракетных и аэрокосмических конструкций из композиционных материалов. — М.: МГТУ им. Н. Э. Баумана, 1998. — С. 507.

2. В.Ф. Суровикин, Ю.В. Суровикин, М.С. Цеханович. Новые направления в технологии получения углерод-углеродных материалов. Применение углерод-углеродных материалов. // Рос. хим. ж-л. (Ж-л Рос. хим. об-ва им. Д. И. Менделеева). 2007. № 4. С. 111–118.

3. Д.В. Дедков, А.В. Зайцев, А.А. Ташкинов. Концентрация напряжений в слое тканого композита с закрытыми внутренними технологическими порами // Вестник ПНИПУ. Механика, 2011. № 4. С. 29–36.

4. Д.В. Дедков, А.А. Ташкинов. Коэффициенты концентрации напряжений в слое тканого композита с локальными технологическими дефектами при чистом формоизменении // Вычислит. механика сплошных сред. 2013. Т. 6, No 1. С. 103--109.

5. Д.В. Дедков, А.В. Зайцев. Концентрация напряжений в слое тканого композита с локальными дефектами при двухосном однородном равнокомпонентном деформировании // Вестник самарского гос. технич. ун-та, 2013. № 4(33). С. 66‑75.

6. А.С. Иманкулова. Текстильные композиты. Бишкек: Изд. центр «МОК», 2005. 152 с.

7. Vincent Bergeaud, Vincent Lefebvre, Etinne Rossignon. SALOME 6. The Open Source integration platform for numerical simulations. – 2012. http://salome-platform.org/user-section/salome-brochure.

8. Ю.М. Тарнапольский, А.В. Розе, И.Г. Жигун, Г.М. Гуняев. Конструкционные особенности материалов, армированных высокомодульными волокнами // Механика полимеров. 1971. № 4. С. 676–685.

Поделиться:

Воспользуйтесь поиском по сайту: