 |
Анализ способов учета особенностей графа мелиоративного объекта
|
|
|
|
Рассматривается мелиоративный объект, на котором планируется провести реконструкцию; варианты реконструкции по каждому объекту реконструкции должны быть выбраны. Постановка и модель задачи выбора проектных вариантов приводится в пункте 2 данного отчета. Задача сформулирована без учета транспортной составляющей. Транспортная составляющая в задачах выбора проектных вариантов должна учитываться в следующих случаях:
1) Экзогенные оценки транспортных задач отсутствуют, поэтому используются или транспортные тарифы (цена реализации транспортных услуг), или себестоимость перевозок, или приведенные затраты на перевозки
2) Выбор конкретного показателя транспортных затрат должен производиться с учетом роли и веса транспортного фактора, степени его влияния на оптимальный план – задача производственная или производственно-транспортная;
3) Показатели транспортных затрат учитывают лишь вновь возникшие затраты на транспортировку.
В производственных задачах транспортный фактор не оказывает влияния на выбор варианта развития и размещения производства. Но если они при этом значительны, то ставится производственно-транспортная задача со слабой транспортной связью.
Перечисленные случаи относятся к обычным транспортным задачам, т.е. задачам транспортировки продукции потребителям или сырья производителям.
Задача, которая является предметом исследования не является ПТЗ с классической транспортной составляющей ввиду особенностей графа формализующего мелиоративную сеть.
На рисунке приводится схема участка магистрального канала с сетью распределительных и участковых каналов. (Пример условный).

Рис. 3.1.
Формализуем сеть следующим образом:
|
|
|
1) Пусть поставщики это узлы сети  , т.е. участки сети, которые подают воду на распределительные и участковые каналы, потребители – узлы сети плюс участки орошения
, т.е. участки сети, которые подают воду на распределительные и участковые каналы, потребители – узлы сети плюс участки орошения 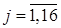 .
.
2) От каждого узла вода может поступать не по всем каналам, а по каким-то определенным. Это условие формализуется введением «матрицы инциденций» - Rij, элемент такой матрицы  , если от узла i вода подается узлу или участку j и
, если от узла i вода подается узлу или участку j и 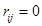 в противном случае.
в противном случае.
 , - (поставщики) узлы сети;
, - (поставщики) узлы сети;
 - (потребители) узлы сети + орошаемые участки;
- (потребители) узлы сети + орошаемые участки;
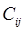 - затраты на транспортировку воды из i в j.
- затраты на транспортировку воды из i в j.
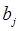 - потребность узла j в орошаемой воде.
- потребность узла j в орошаемой воде.
 - количество оросительной воды, которое может выйти из узла i.
- количество оросительной воды, которое может выйти из узла i.
 .
.
m =8, n = 16;
Аналогия с транспортной задачей
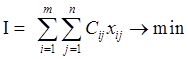
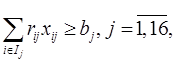
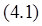
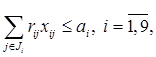
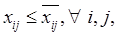
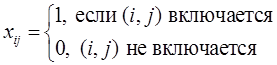 .
.
Принимаем, что от каждого узла вода идет к каждому другому узлу нижних уровней иерархии сети.
Составим матрицу инциденций (R):
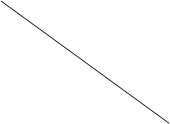 Потребители, i
Поставщики, j Потребители, i
Поставщики, j
| |||||||||||||||||
Схема, построенная по матрице инциденций:
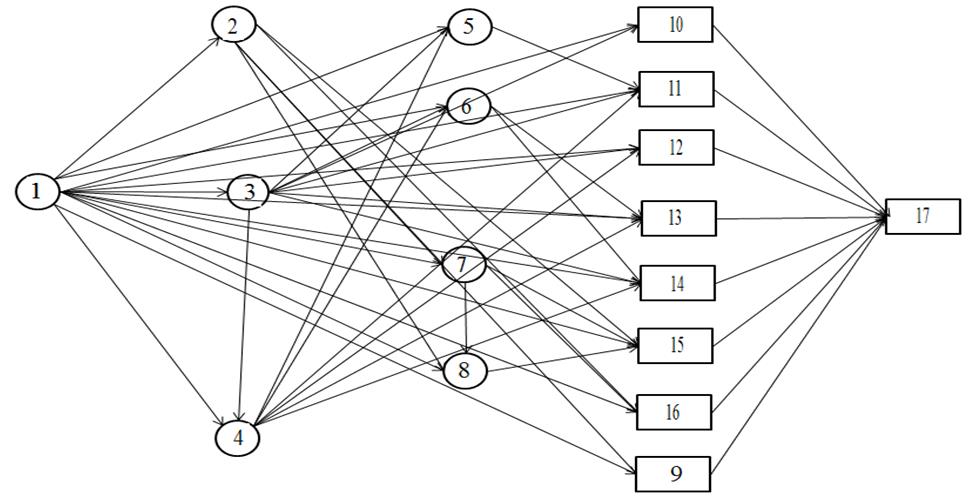
Рис.3.2
Соотнесем формализованную выше сеть с существующими классами сетей. Для формализации направленного графа с пропускными способностями ребер используется инструментарий транспортных сетей. Приведем основные классы транспортных сетей:
|
|
|
Основные понятия и определения транспортных сетей.
В матричных постановках транспортных задач предполагается, что в каждой из задач имеются только пункты производства и пункты потребления, причем перевозки от пунктов потребления к пунктам производства невозможны.
На рисунке 3.3а) представлено графическое изображение транспортной задачи двумя пунктами производства и тремя пунктами потребления, в которой каждая пара пунктов соединена коммуникацией. На рисунке 3.3 б) изображена транспортная задача с запретами, т.е. существуют пункты производства и пункты потребления, между которыми невозможны перевозки. В обеих задачах коммуникации изображаются стрелками, идущими от пунктов производства к пунктам потребления, что означает запрет на перевозку в обратном направлении.
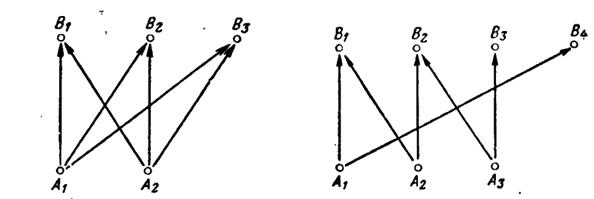
Рис.3.3
Целесообразно расширить постановку транспортных задач так, чтобы в нее укладывались модели, коммуникации которых имеют структуру как на рисунке 3.4. Данная система коммуникаций содержит 8 пунктов. В пункт Р2 можно только ввозить продукцию, а из Р7 только вывозить. Остальные пункты имеют возможность, как ввозить, так и вывозить продукцию.
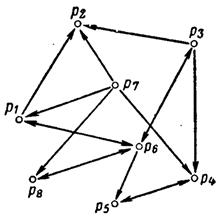
Рис.3.4
Набор двух множеств Р и К называют транспортной сетью  где элементы
где элементы  множества Р являются пунктами транспортной сети, элементы
множества Р являются пунктами транспортной сети, элементы 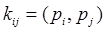 множества К коммуникациями сети. Коммуникация
множества К коммуникациями сети. Коммуникация  связывает пункты
связывает пункты  и
и  .
.
Транспортная сеть, порожденная некоторыми подмножествами множеств P и K, называется подсетью транспортной сети  .
.
1. Формализация транспортных сетей в виде матриц.
Транспортные сети могут задаваться с помощью матриц. Допустим, что транспортная сеть  содержит n пунктов. Рассмотрим квадратную матрицу R порядка n однозначно определяющую породившую её транспортную сеть
содержит n пунктов. Рассмотрим квадратную матрицу R порядка n однозначно определяющую породившую её транспортную сеть  . Элементы
. Элементы  матрицы R вычисляются согласно правилу
матрицы R вычисляются согласно правилу
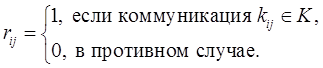
Например, матрица сети изображенной на рис. 3.4 имеет вид

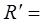
Просматривая строку матрицы 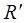 можно выяснить, в какие пункты допускается транспортировка из пункта, соответствующего данной строке. По столбцам матрицы можно выявить коммуникации, заканчивающиеся в фиксированных пунктах. Строки матрицы отвечают пунктам потребления, а столбцы соответствуют пунктам производства. На главной диагонали матрицы транспортной сети всегда стоят нули, так как по определению не существует коммуникаций, которые начинаются и заканчиваются в одном и том же пункте.
можно выяснить, в какие пункты допускается транспортировка из пункта, соответствующего данной строке. По столбцам матрицы можно выявить коммуникации, заканчивающиеся в фиксированных пунктах. Строки матрицы отвечают пунктам потребления, а столбцы соответствуют пунктам производства. На главной диагонали матрицы транспортной сети всегда стоят нули, так как по определению не существует коммуникаций, которые начинаются и заканчиваются в одном и том же пункте.
|
|
|
2. Связная максимальная сеть.
Транспортную сеть называют связной, если любая пара её пунктов может быть связана с помощью некоторого маршрута этой сети. Связная подсеть транспортной сети  называется максимальной, если она содержит вместе с любым пунктом pi пункт
называется максимальной, если она содержит вместе с любым пунктом pi пункт 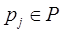 связанной с
связанной с  некоторой коммуникацией
некоторой коммуникацией 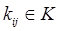 , а также все коммуникации множества K, которые соединяют пункты подсети. На рисунке 3.5 приведены примеры связных и несвязных сетей.
, а также все коммуникации множества K, которые соединяют пункты подсети. На рисунке 3.5 приведены примеры связных и несвязных сетей.

Рис.3.5
3. Направленная связная сеть.
Если каждая пара пунктов транспортной сети может быть связана направленным маршрутом, то сеть называют направленно связной. Любая направленно связная сеть является связной. Обратное утверждение неверно, т.к. существуют связные сети, не являющиеся направленно связными. Пример такой сети изображен на рисунке 3.5 а). Пример направленно связной сети представлен на рисунке 3.5 б).
4. Характеристики коммуникаций (функции на сетях)
Рассматривается ряд функций, определенных на множестве пунктов сети или множестве коммуникаций сети.
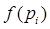 действительная функция пунктов
действительная функция пунктов 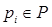 ,
,
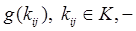 действительная функция, определенная на множестве коммуникаций K.
действительная функция, определенная на множестве коммуникаций K.
Перечислим функции, которые обычно используются в задачах, связанных с транспортными сетями:
1) функция производства и потребления  задается на множестве Р всех пунктов сети
задается на множестве Р всех пунктов сети  . Если
. Если 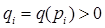 , то пункт
, то пункт 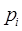 называется пунктом производства, при
называется пунктом производства, при  пункт
пункт 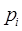 называется пунктом потребления. Пункт
называется пунктом потребления. Пункт 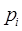 , для которого
, для которого  , называется перевалочным пунктом.
, называется перевалочным пунктом.
2) функция пропускных способностей коммуникаций 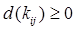 задается на множестве К коммуникаций транспортной сети
задается на множестве К коммуникаций транспортной сети  . Значение функции пропускных способностей на коммуникации
. Значение функции пропускных способностей на коммуникации 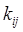 равно предельному количеству продукта, которое может быть перевезено по этой коммуникации. Число
равно предельному количеству продукта, которое может быть перевезено по этой коммуникации. Число 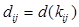 называется пропускной способностью коммуникации
называется пропускной способностью коммуникации 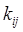 . Если вдоль данной коммуникации может быть перевезено любое количество продукта, то её пропускная способность полагается равной бесконечности. Если сеть не содержит коммуникацию проходящую из одного пункта в другой, то можно считать, что пропускная способность равна нулю.
. Если вдоль данной коммуникации может быть перевезено любое количество продукта, то её пропускная способность полагается равной бесконечности. Если сеть не содержит коммуникацию проходящую из одного пункта в другой, то можно считать, что пропускная способность равна нулю.
|
|
|
3) Рассматривается сеть  , на множестве коммуникаций которой определена функция пропускных способностей
, на множестве коммуникаций которой определена функция пропускных способностей  . Выделим два пункта сети источник -
. Выделим два пункта сети источник - 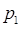 и сток -
и сток - 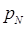 .
. 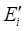 – множество коммуникаций сети, выходящих из пункта
– множество коммуникаций сети, выходящих из пункта 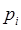 , а
, а  - множество коммуникаций, заканчивающихся в пункте
- множество коммуникаций, заканчивающихся в пункте 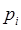 .
.
Функция  , определенная на множестве К, для которой имеют место соотношения
, определенная на множестве К, для которой имеют место соотношения




называется потоком на сети, совместимым с функцией  и направленным из
и направленным из 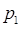 в
в 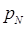 .
.
Функция  неотрицательна, вследствие чего ее можно называть арифметическим потоком.
неотрицательна, вследствие чего ее можно называть арифметическим потоком.
Функция 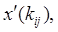 , определенная на множестве коммуникаций
, определенная на множестве коммуникаций  и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
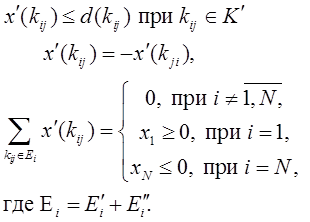
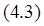
называется алгебраическим потоком, совместимым с функцией 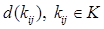 . Каждому арифметическому потоку отвечает алгебраический поток, совместимый с той же функцией пропускных способностей.
. Каждому арифметическому потоку отвечает алгебраический поток, совместимый с той же функцией пропускных способностей.
4) Функция 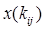 , определенная на множестве коммуникаций K для которой справедливы соотношения
, определенная на множестве коммуникаций K для которой справедливы соотношения
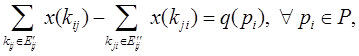

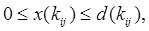
Называется планом перевозок, совместимым с функцией производства и потребления  и функцией пропускных способностей
и функцией пропускных способностей 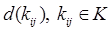 . В соответствии с соотношениями
. В соответствии с соотношениями  план перевозок
план перевозок 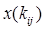 совместимый с
совместимый с  и
и  , представляет собой набор перевозок по коммуникациям сети, который позволяет удовлетворить запросы всех пунктов за счет возможностей пунктов производства данной сети, не выходя за пределы пропускных способностей ее коммуникаций. Как и в случае потоков, системы перевозок могут задаваться в виде арифметических планов, либо в виде алгебраических планов.
, представляет собой набор перевозок по коммуникациям сети, который позволяет удовлетворить запросы всех пунктов за счет возможностей пунктов производства данной сети, не выходя за пределы пропускных способностей ее коммуникаций. Как и в случае потоков, системы перевозок могут задаваться в виде арифметических планов, либо в виде алгебраических планов.
5) Для сравнения планов перевозок с точки зрения транспортных затрат, связанных с их реализацией служит функция транспортных расходов 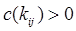 , определенная на множестве коммуникаций сети
, определенная на множестве коммуникаций сети  Значение функции
Значение функции  на коммуникации
на коммуникации 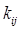 равно стоимости перевозки единицы однородного продукта вдоль
равно стоимости перевозки единицы однородного продукта вдоль  . Число
. Число  называют величиной транспортных расходов коммуникации
называют величиной транспортных расходов коммуникации 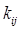 . Функции
. Функции  , определенные на множествах коммуникаций, могут задаваться непосредственно на транспортной сети или в виде квадратных матриц порядка N (число пунктов сети ).
, определенные на множествах коммуникаций, могут задаваться непосредственно на транспортной сети или в виде квадратных матриц порядка N (число пунктов сети ).
Метод Минти
Методом Минти решается задача построения дерева кратчайших путей на сети с корнем в фиксированной вершине. Алгоритм состоит из конечного числа шагов, на каждом из которых отражаются вершины сети и выделяются некоторые ее дуги.
Пусть p1 – произвольный пункт сети  . Требуется для любого пункта
. Требуется для любого пункта 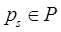 найти оптимальный маршрут, идущий от
найти оптимальный маршрут, идущий от 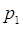 к
к  .
.
Алгоритм метода Минти
|
|
|
0. На предварительном (нулевом) этапе алгоритма:
- формируется массив значений дуг
 - значения транспортных расходов для коммуникации
- значения транспортных расходов для коммуникации 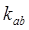 , которые перед началом первой итерации полагаются равными
, которые перед началом первой итерации полагаются равными  ≥0;
≥0;
- осуществляется отметка вершины p1= I числом
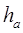 = 0,
= 0,
Стандартная итерация включает этапы:
1. Отметка вершин сети.
Рассматриваются коммуникации, которые начинается в одном из уже отмеченных её пунктов, и оканчивающиеся в еще неотмеченных пунктах сети. Для каждой такой коммуникации - 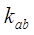 вычисляется
вычисляется  .
.
2. Из рассмотренных коммуникаций выделяются те, которым соответствует минимальное значение суммы

где 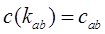
 - множество уже отмеченных пунктов сети.
- множество уже отмеченных пунктов сети.
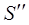 - множество еще не отмеченных пунктов сети.
- множество еще не отмеченных пунктов сети.
При выделении учитывается, что из нескольких коммуникаций, подлежащих выделению и заканчивающихся в одном пункте, выделяется только одна любая.
3. Отмечаются концы выделенных коммуникаций – каждому из них сопоставляется минимальное значение суммы.
Процесс длится до тех пор, пока на очередном шаге станет невозможным дальнейшее расширение множества отмеченных пунктов. Затем происходит переход к следующей итерации.
4. Последовательность выделенных коммуникаций, образованная в процессе движения до пункта 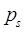 , составляет маршрут
, составляет маршрут  с началом в пункте
с началом в пункте 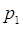 и концом
и концом  .
.
Путь, построенный по методу Минти, будет кратчайшим. Это можно доказать с помощью индукции по номеру итерации, на которой была помечена вершина t, или, по количеству дуг, составляющих кратчайший путь. Если это произошло на первом шаге, то доказываемое утверждение очевидно. Предположим, что оно верно для всех пунктов, помеченных за первые r итераций, т. е. тех, которые достигаются переходом по r дугам. Тогда, если конечная вершина t помечена на (r + 1)-ой итерации, то полученный путь также будет кратчайшим, так как данная вершина помечается в результате минимально возможного продолжения одного из путей, полученного за предыдущие r итераций и являющегося по предположению кратчайшим.
Если некоторый пункт  не попал в число отмеченных, то это указывает на невозможность сформировать направленный маршрут сети, начинающийся в
не попал в число отмеченных, то это указывает на невозможность сформировать направленный маршрут сети, начинающийся в 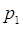 и концом
и концом  .
.
Список используемой литературы
1. Оросительные системы России: от поколения к поколению: монография / В. Н. Щедрин, А. В. Колганов, С. М. Васильев, А. А. Чураев. – В 2 ч. –
Ч. 1. – Новочеркасск: Геликон, 2013. – 283 с.
2. Шумаков, Б. А. Орошаемое земледелие // Б. А. Шумаков. - М.: Россельхозиздат, 1965.-81 с.
3. Костяков А.Н. Основы мелиорации 6-е изд., испр. и доп. – М.:Сельхозгиз 1938. – 732 с.
4. Рекомендации по реконструкции и модернизации мелиоративных систем (на примере Ростовской области) подготовлены сотрудниками ФГБНУ «РосНИИПМ»: кандидатом технических наук А. А Чураевым; доктором технических наук Ю. Ф. Снипич; кандидатом технических наук Т. А. Погоровым; кандидатом технических наук А. Е. Шепелевым; Л. В. Юченко; М. В. Вайнберг; В. В. Митровым.
5. А. А. Кувалкин, А. В. Кувалкин, Б. Х. Санжапов, М. В. Середа «Планирование водопользования в территориально распределенной мелиоративной системе на имитационной модели».
6. https://ru.wikipedia.org/wiki/Большой Ставропольский канал.
7.http://cyberleninka.ru/ Научная электронная библиотека «киберленинка».
8.Гузыкина Т.Н. «Моделирование и оптимизация производственных процессов» для студентов формы обучения экстернат./Юж.-Рос.гос. техн. Ун-т –Новочеркасск: ЮРГТУ, 2007-70с.
9.Е.Г. Гольштейн, Д.Б.Юдин «Задачи линейного программирования транспортного типа» - М., 1969 г., 384 с.
|
|
|


