 |
Курсовая работа по дисциплине «Теория автоматического управления»
|
|
|
|
Задание:
1. В соответствии с вариантом задания (таблица 1) по переходной характеристике определить математическую модель объекта управления в виде передаточной функции WОУ(s). Описать и графически рассчитать все числовые параметры передаточной функции WОУ(s) (например, транспортное запаздывание τ, постоянную времени Т, коэффициент передачи k). Объяснить, как влияет каждый параметр на вид переходного процесса.
2. Для схемы, представленной на рис. 1, определить эквивалентную передаточную функцию замкнутой и разомкнутой системы и сделать выводы об устойчивости для каждого случая. Аргументировать, полученные выводы, основываясь на корневом методе устойчивости. Привести графики, на которых показано расположение полюсов характеристического полинома для замкнутой и разомкнутой систем. Передаточная функция датчика WДАТ(s) представлена в таблице 2. Передаточную функцию регулятора WРЕГ(s) принять равной 1.
3. Рассчитать эквивалентную передаточную функцию объекта управления и датчика WДОУ(s) (рис. 1) и построить переходную характеристику. По переходной характеристике WДОУ(s) рассчитать параметры смещения «a» и транспортного запаздывания «τ» (эти параметры необходимы при расчете ПИД-регулятора методом Зиглера-Никольса и методом CHR). Пример переходной характеристики показан на рис. 2. В соответствии с вариантом задания рассчитать коэффициенты ПИД-регулятора (таблица 3) и построить переходную характеристику для системы управления с ПИД-регулятором. Сделать вывод о качественных показателях переходного процесса (времени управления, статической ошибке, перерегулировании, количестве колебаний и т.д.). Произвести ручную подстройку коэффициентов ПИД-регулятора с целью улучшения качества переходного процесса.
|
|
|
4. Разработать структурную и электрическую схемы системы управления, если в качестве регулятора используется блок Р-27 комплекса Каскад-2. В качестве исполнительного механизма использовать двигатель переменного тока с постоянной скоростью вращения вала (см. пример ниже). Пояснить тип обратной связи в блоке Р-27 при реализации полученного регулятора.
5. Сделать выводы о проделанной работе.
Порядок выполнения работы:
| Вариант 3 |
|
Рисунок 1- Переходные характеристики объектов управления.
Таблица 1 Передаточная функция датчика WДАТ(s)
| Вариант 3 |
|
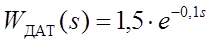
Таблица 2 Метод расчет коэффициентов ПИД-регулятора
| Вариант 3 |
| Метод Зиглера-Никольса |
Математическая модель ОУ задается следующим образом:
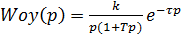(1)
где сама функция задается как идеальное интегрирующее звено с замедлением в виде:
(2)
где k – коэффициент передачи звена, который задает наклон переходной характеристики и, соответственно, скорость нарастания выходного сигнала;
Т - постоянная времени, которая определяет перегиб переходной характеристики на начальном участке;
τ – транспортное запаздывание, которое характеризует инерционность звена или временную задержку между входом и выходом.
Транспортное запаздывание τ примерно равно 0,03 с. Из графика видно, что за каждые 0,03 с выходной параметр объекта возрастает на 0,15. Следовательно, коэффициент передачи k=0,15/0,03=5 (т.е. за каждую секунду выходной сигнал будет увеличиваться на 5). Постоянную времени Т определим, проведя касательную в точке перегиба. Интервал на оси времени, который отсечет эта касательная и будет постоянной времени Т. В нашем случае Т=0,07 с.
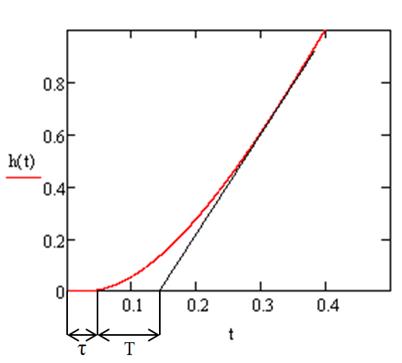
Рисунок 2 - Переходная характеристика объекта управления.
Таким образом, передаточная функция объекта управления имеет вид:
|
|
|
(3)
На рисунке 3 показана структурная схема системы управления, смоделированная в программе LabVIEW.
Рисунок 3 - Структурная схема замкнутой системы управления.
Учитывая данные выше запишем эквивалентные передаточные функции для замкнутой и разомкнутой системы.
Эквивалентная передаточная функция для замкнутой системы:
(4)
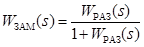(5)
Проверили правильность расчетов с помощью LabVIEW и построили корневой годограф для каждого случая. Рассмотрим сначала разомкнутую систему WРАЗ(s). На рис. 5 показана лицевая панель программы и ее графический код.
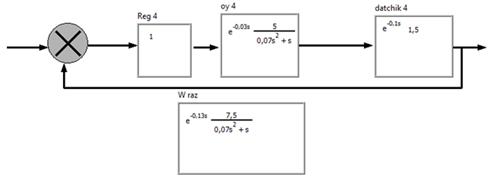
Рисунок 4 – Структурная схема разомкнутой системы.
Рисунок 5 – Годограф разомкнутой системы.
Рисунок 6 - Модель разомкнутой системы управления в LabVIEW.
Как видно из рисунка 5, корни характеристического полинома разомкнутой системы содержать корни s1=-14.2, s2=0. Корень s1 имеет отрицательную действительную часть и удовлетворяет корневому критерию устойчивости. А вот корень s2 равен 0 и потому вся система становится неустойчивой, в чем можно убедиться по графику переходного процесса (рисунок 7).
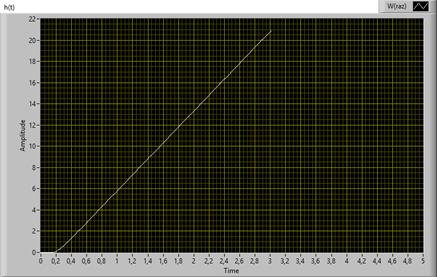
Рисунок 7 – Переходной процесс для разомкнутой системы управления.
Теперь оценим устойчивость замкнутой системы WЗАМ(s). На рисунке 8 показана лицевая панель программы.
Рисунок 8 – Структурная схема замкнутой системы.
Рисунок 9 – Годограф замкнутой системы.
Рисунок 10 - Модель замкнутой системы управления в LabVIEW.
Как видно из рисунка 9, корни характеристического полинома замкнутой системы содержать корни s1,2=-7,1±7,5*i. Оба корня имеют отрицательную действительную часть и потому замкнутая система устойчива. В этом можно убедиться, проанализировав переходной процесс (рисунок 11).
Рисунок 11 – Переходной процесс на выходе замкнутой системы управления.
По формуле последовательного соединения звеньев, найдем эквивалентную передаточную функцию объекта управления WОУ(s) и датчика WДАТ(s).
(6)
Теперь для расчета коэффициентов ПИД-регулятора методом Зиглера-Никольса построили переходной процесс для WДОУ(s) и определили смещение «а» и транспортное запаздывание «τ». Для рассматриваемой передаточной функции а=1,75; τ=0,13. Из таблицы 4 определим коэффициенты ПИД-регулятора.
|
|
|
Таблица 3 - Метод Зиглера-Никольса
| Регулятор | Расчет по отклику на скачок | ||
| К | ТИ | ТД | |
| П | 1/а | - | - |
| ПИ | 0,9/а | 3τ/К | - |
| ПИД | 1,2/а | 0,9τ/К | 0,5τК |
Таблица 4 – Расчет коэффициентов регулятора методом Зиглера-Никольса
| Регулятор | Расчет по отклику на скачок | ||
| К | ТИ | ТД | |
| П | 0,57 | - | - |
| ПИ | 0,51 | 0,76 | - |
| ПИД | 0,68 | 0,17 | 0,04 |
Учитывая коэффициенты, полученные выше, построим переходную характеристику для каждого регулятора.
Рисунок 12 - Переходная характеристика для П,ПИ и ПИД регуляторов.
Из рисунка 12 видно, что наиболее благоприятным в смысле обеспечения качества переходного процесса, является П-регулятором с параметрами: К=0,57.
Учитывая, что метод Зиглера-Никольса является приближенным методом настройки регуляторов, попробуем вручную, экспериментально подкорректировать коэффициент пропорциональной составляющей П-регулятора.
На рис. 9 показаны переходные процессы для системы управления с варьируемым коэффициентом пропорциональности К1=3; К2=0.57; К3=0,6. Из рис. 9 видно, что наиболее благоприятным в смысле обеспечения качества переходного процесса, является П-регулятор с параметрам: К=0.57.
Рисунок 13 - Экспериментальная настройка П-регулятора: варьирование коэффициента пропорциональности К.
Т.к. выше указано, что для данной системы наилучшим регулятором будет П-регулятор, составим структурную схему системы управления с данным фактом.
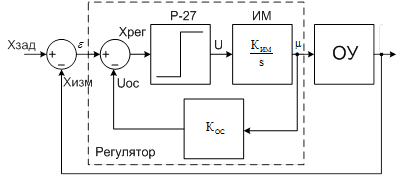
Рисунок 14 Структурная схема САР с П-регулятором.
Сигнал рассогласования поступая в регулятор Р-27 формирует напряжение, которое влияет на запуск электродвигателя. Далее сигнал по ОС поступает в 
а после на сумматор в виде отрицательного значения, где сигнал ошибки и ОС представляют собой разность, т.е. ХРЕГ=e-Uoc, где Uoc=КOC∙μ. Как только сигнал становится меньше половинной зоны нечувствительности и упреждением β ИМ отключается и регулирующий орган арматуры останавливается, если же сигнал изменится и станет больше данного значения, то механизм снова включится, стремясь уменьшить рассогласование. Таким образом, импульсный регулятор Р-27 с исполнительным механизмом постоянной скорости, охваченный отрицательной обратной связью по положению регулирующего органа μ, реализует П-закон регулирования с коэффициентом КП=1/КОС.
Вывод: в данной работе мы научились описывать элементы линейной САУ, определять качественные показатели и качество управления системой, разумели как освоить расчет оптимальных коэффициентов регулятора а также разрабатывать структурные схемы САУ.
|
|
|
|
|
|
