Запись числа в десятичной системе счисления

Как известно, в десятичной системе счисления для записи чисел используется 10 знаков (цифр): 0,1, 2, 3,4, 5, 6, 7, 8, 9. Из них образуются конечные последовательности, которые являются краткими записями чисел. Например, последовательность 3745 является краткой записью числа 3·10³ + 7·10² + 4·10 + 5.

Определение. Десятичной записью натурального числа х называется его представление в виде: х = a_n·10ⁿ+a_n-1·10^n-1+... + а₁·10 + а₀, где коэффициенты a_n, a_n-1, …, а₁, а₀, принимают значения 0,1, 2, 3, 4, 5, 6, 7,8,9 и а_n≠0.

Сумму a_n·10ⁿ+a_n-1·10^n-1+... + а₁·10 + а₀ в краткой форме принято записывать так: .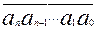

Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натурального числа надо доказывать.

Теорема. Любое натуральное число х можно представить в виде:

х=a_n·10ⁿ+a_n-1·10^n-1+... + а₁·10 + а₀ (1),

где а_n, а _{n -1},...,а₁,а₀ принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8,9, и такая запись единственна.

Доказательство существования записи числа х в виде (1). Среди последовательных чисел 1,10,10²,10³,..., 10ⁿ,... найдем наибольшую степень, содержащуюся в х, т.е. такую что 10ⁿ ≤х < 10ⁿ⁺¹, что всегда можно сделать.

Разделим (с остатком) число х на 10ⁿ. Если частное этих чисел обозначить через a_n, а остаток через х_n, тo x =а_n·10ⁿ+х_n, где a_n< 10 и х_n < 10ⁿ. Далее, разделив х_n на 10^n-1, получим: х_n = a_n-1 · 10^n-1 + х_n-1, откуда х = а_n · 10ⁿ + a_{n-1 +} х_n-1, где a_n-1< 10 и х_n-1< 10^n-1 . Продолжая деление, дойдем до равенства х₂ = а₁ ·10+ х₁. Положив х₁ = а₀, будем иметь х = a_n · 10ⁿ+ a_n-1 · 10^n-1 +… + a₁ ·10+а₀, т.е. число х будет представлено в виде суммы степеней числа 10 с коэффициентами, меньшими 10, что и означает возможность записи числа х в десятичной системе счисления.

Доказательство единственности представления числа х в виде (1). Число n в равенстве (1) однозначно определяется условием 10ⁿ ≤ х < 10ⁿ⁺¹. После того как n определено, коэффициент a_n находят из условия: a_n·10ⁿ ≤ х < (a_n+1)·10ⁿ. Далее, аналогичным образом определяются коэффициенты a_n-1,…, а_0.

Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.

Теорема. Пусть х и у - натуральные числа, запись которых дана в десятичной системе счисления:

х = a_n · 10ⁿ+ a_n-1 · 10^n-1+…+ а₁ ·10+ а₀,

у= b_m·10^m+b_m-1·10^m-1+…+b₁·10+b₀

Тогда число х меньше числа у, если выполнено одно из условий:

а) n < m;

б) n = m, но a_n <b_n;

в) n=m, a_n= b_n,..., а_к = b_к, но а_к-1 < b_к-1.

Доказательство. В случае а) имеем: так как n < m, то 10ⁿ⁺¹≤10^m, а поскольку х ≤10ⁿ⁺¹ и 10^m ≤у, то х<10ⁿ⁺¹≤10^m≤у, т.е. х<у.

В случае б): если n = m, но а_n < b_n, то a_n+ 1 ≤b_n и потому (a_n+ 1) ·10ⁿ≤b_n·10ⁿ. А так как х < (a_n+ 1) ·10ⁿ и bⁿ·10ⁿ≤у, то х <(a_n+1) ·10ⁿ< b_n·10ⁿ≤у, т.е. х<у.

Аналогично доказывается теорема и в случае в).

Например, если х =3456, а у = 3467, то х < у, так как число тысяч и сотен в записи одинаковое, но десятков в числе х меньше, чем десятков в числе у.

Если натуральное число х представлено в виде х = a_n·10ⁿ + a_n-1·10^n-1 +... + a₁·10+а_о, то числа 1, 10, 10²,..., 10ⁿ называют разрядными единицами соответственно первого, второго,..., n + 1 разряда, причем 10 единиц одного разряда составляют одну единицу следующего высшего разряда, т.е. отношение соседних разрядов равно 10 - основанию системы счисления.

Три первых разряда в записи числа соединяют в одну группу и называют первым классом, или классом единиц. В первый класс входят единицы, десятки и сотни.

Четвертый, пятый и шестой разряды в записи числа образуют второй класс - класс тысяч. В него входят единицы тысяч, десятки тысяч и сотни тысяч.

Затем следует третий класс - класс миллионов, состоящий тоже из трех разрядов: седьмого, восьмого и девятого, т.е. из единиц миллионов, десятков миллионов и сотен миллионов.

Последующие три разряда также образуют новый класс и т.д. Выделение классов единиц, тысяч, миллионов и т.д. создает удобства для записи и прочтения чисел.

В десятичной системе всем числам можно дать название (имя). Это достигается следующим образом: имеются названия первых десяти чисел, затем из них в соответствии с определением десятичной записи и путем прибавления еще немногих слов образуются названия последующих чисел. Так, числа второго десятка (они представляются в виде 1·10 + а₀) образуются из соединения первых десяти названий и несколько измененного слова десять («дцать»):

одиннадцать - один на десять,

двенадцать - два на десять и т.д.

Может быть, естественнее было бы говорить «два и десять», но наши предки предпочли говорить «два на десять», что и сохранилось в речи.

Слово «двадцать» обозначает два десятка.

Числа третьего десятка (это числа вида 210 + а0) получают путем прибавления к слову «двадцать» названий чисел первого десятка: двадцать один, двадцать два и т.д.

Продолжая далее счет, получим название чисел четвертого, пятого, шестого, седьмого, восьмого, девятого и десятого десятков. Названия этих чисел образуются так же, как и в пределах третьего десятка, только в трех случаях появляются новые слова: сорок (для обозначения четырех десятков), девяносто (для обозначения девяти десятков) и сто (для обозначения десяти десятков). Названия чисел второй сотни составляются из слова «сто» и названий чисел первого и последующих десятков. Таким путем образуются наименования: сто один, сто два,..., сто двадцать и т.д. Отсчитав новую сотню, будем иметь две сотни, которые для краткости называют «двести». Для получения чисел, больших двухсот, снова воспользуемся названиями чисел первого и последующих десятков, присоединяя их к слову «двести». Затем получим особые названия: триста, четыреста, пятьсот и т.д. до тех пор, пока не отсчитаем десять сотен, которые носят название тысяча.

Счет за пределами тысячи ведется так: прибавляя к тысяче по единице (тысяча один, тысяча два и т.д.), получим две тысячи, три тысячи и т.д. Когда же отсчитаем тысячу тысяч, то это число получит особое наименование - миллион. Далее считаем миллионами до тех пор, пока не дойдем до тысячи миллионов. Полученное новое число - тысяча миллионов - носит особое название миллиард. Миллион миллионов называется биллионом. В вычислениях миллион принято записывать в виде 10⁶, миллиард - 10⁹, биллион - 10¹². По аналогии можно получить записи еще больших чисел: триллион - 10¹⁵, квадриллион - 10¹⁸ и т.д.

Таким образом, для того чтобы назвать все натуральные числа в пределах миллиарда, потребовалось только 16 различных слов: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, сорок, девяносто, сто, тысяча, миллион, миллиард. Остальные названия чисел (в пределах миллиарда) образуются из основных.

Вопросы наименования и записи чисел рассматриваются в начальном курсе математики в разделе «Нумерация». При этом десятичной записью натурального числа считают его представление в виде суммы разрядных слагаемых. Например, 3000 + 700 + 40 + 5 есть сумма разрядных слагаемых числа 3745. Представление числа в виде таких сумм удобно для его наименования: три тысячи семьсот сорок пять.

Алгоритм сложения

Сложение однозначных чисел можно выполнить, основываясь на определении этого действия, но чтобы всякий раз не обращаться к определению, все суммы, которые получаются при сложении однозначных чисел, записывают в особую таблицу, называемую таблицей сложения однозначных чисел, и запоминают.

Естественно, смысл сложения сохраняется и для многозначных чисел, но практическое выполнение сложения происходит по особым правилам. Сумму многозначных чисел обычно находят, выполняя сложение столбиком. Например,

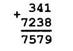
Выясним, каким образом возникает этот алгоритм, какие теоретические положения лежат в его основе.

Представим слагаемые 341 и 7238 в виде суммы степеней десяти с коэффициентами:

341 + 7238 = (3·10² + 4·10 + 1) + (7·10³ + 2·10² + 3·10 + 8).

Раскроем скобки в полученном выражении, поменяем местами и сгруппируем слагаемые так, чтобы единицы оказались рядом с единицами, десятки с десятками и т.д. Все эти преобразования можно выполнить на основании соответствующих свойств сложения. Свойство ассоциативности разрешает записать выражение без скобок:

3·10² + 4·10 + 1 + 7·10³ + 2·10² + 3·10 + 8.

На основании свойства коммутативности поменяем местами слагаемые: 7·10³ + 3·10² + 2·10² + 4·10 + 3·10 + 1 + 8. Согласно свойству ассоциативности произведем группировку: 7·10³ + (3·10² + 2·10²) + (4·10 + 3·10) + (1 + 8). Вынесем за скобки в первой выделенной группе число 10², а во второй - 10. Это можно сделать в соответствии со свойством дистрибутивности умножения относительно сложения:

7·10³ + (3 + 2) ·10² + (4 + 3) ·10 + (1 + 8).

Итак, сложение данных чисел 341 и 7238 свелось к сложению однозначных чисел, изображенных цифрами соответствующих разрядов. Эти суммы находим по таблице сложения: 7·10³ + 5·10² + 7·10 + 9. Полученное выражение есть десятичная запись числа 7579.

Видим, что в основе алгоритма сложения многозначных чисел лежат следующие теоретические факты:

- способ записи чисел в десятичной системе счисления;

- свойства коммутативности и ассоциативности сложения;

- дистрибутивность умножения относительно сложения;

- таблица сложения однозначных чисел.

Нетрудно убедиться в том, что в случае сложения чисел «с переходом через десяток» теоретические основы алгоритма сложения будут теми же. Рассмотрим, например, сумму 748 + 436.

Представим слагаемые в виде суммы степеней десяти с соответствующими коэффициентами: (7·10² + 4·10 + 8) + (4·10² + 3·10 + 6). Воспользуемся свойствами сложения и дистрибутивностью умножения относительно сложения и преобразуем полученное выражение к такому виду: (7 + 4) ·10² + (4 + 3) ·10 + (8 + 6). Видим, что в этом случае сложение данных чисел также свелось к сложению однозначных чисел, но суммы 7 + 4, 8 + 6 превышают 10 и поэтому последнее выражение не является десятичной записью числа. Необходимо сделать так, чтобы коэффициенты перед степенями 10 оказались меньше 10. Для этого выполним ряд преобразований. Сначала сумму 8 + 6 представим в виде 1·10 +4:

(7 + 4) ·10² + (4 + 3) ·10 + (1·10 + 4).

Затем воспользуемся свойствами сложения и умножения и приведем полученное выражение к виду: (7+4) ·10²+ (4+3+1) ·10+4. Суть последнего преобразования такова: десяток, который получился при сложении единиц, прибавим к десяткам данных чисел. И наконец, записав сумму 7 + 4 в виде 1·10 + 1, получаем: (1·10 + 1) ·10² + 8·10 + 4. Последнее выражение есть десятичная запись числа 1184. Следовательно, 748 + 436 = 1184.

Выведем алгоритм сложения многозначных чисел в общем виде. Пусть даны числа: х = a_n·10ⁿ+ a_n-1·10^n-1+... + а₀ и у = b_n·10ⁿ+b_n-1·10^n-1+…+b₀, т.е. рассмотрим случай, когда количество цифр в записи чисел х и у одинаково, х + у = = (a_n·10ⁿ+ a_n-1·10^n-1+... + а₀) + (b_n·10ⁿ+b_n-1·10^n-1+…+b₀) = (а_n+ b_n)·10ⁿ + (a_n-1+b _n-1) · 10^n-1 +... + (а₀ + b₀) - преобразования выполнены на основе свойств ассоциативности и коммутативности сложения, а также дистрибутивности умножения относительно сложения. Сумму (a_n+ b_n) · 10ⁿ + (a_n-1 + b_n-1) · 10^n-1+... + (а₀ + b₀), вообще говоря, нельзя рассматривать как десятичную запись числа х + у, так как коэффициенты перед степенями 10 могут быть больше 9. Лишь в случае, когда все суммы а_к + b_к не превосходят 9, операцию сложения можно считать законченной. В противном случае выбираем наименьшее k, для которого а_k + b_k ≥10. Если а_k + b_k ≥10, то из того, что 0 ≤а_к ≤9 и 0 ≤ b_к ≤ 9, следует неравенство 0 ≤ а_к + b_к ≤18 и поэтому а_к + b_к можно представить в виде а_к + b_к =10 + с_к, где 0 ≤ с_к ≤ 9. Но тогда (а_к + b_к) ·10^к = (10 + с_к) ·10^к = 10^k+1 + с_к ·10^k. В силу свойств сложения и умножения в (a_n+ b_n) · 10ⁿ+…+(а₀+ b₀) слагаемые (a_k+1+ b_k+l) · 10^k+1 +(a_k + b_k) ·10^k могут быть заменены на (a_k+1+ b_k+l + 1) · 10ⁿ⁺¹ + с_к · 10^k. После этого рассматриваем коэффициенты а_n+ b_n, a_n-1+ b_n-1,..., а_к+2+ b_к+1, a_k+1+ b_k+1+ 1, выбираем наименьшее s, при котором коэффициент больше 9, и повторяем описанную процедуру. Через n шагов придем к выражению вида: х + у = (с_n+10) · 10ⁿ +... + с₀, где с_n≠ 0, или х + у = 10ⁿ⁺¹+ с_n · 10ⁿ +... + с₀, и где для всех n выполняется равенство 0 ≤ с_n < 10. Тем самым получена десятичная запись числа х + у.

В случае когда десятичные записи слагаемых имеют разное количество цифр, надо приписать к числу, имеющему меньшее количество цифр, несколько нулей впереди, уравняв количество цифр в обоих слагаемых. После этого применяется описанный выше процесс сложения. Он позволяет сформулировать в общем виде алгоритм сложения натуральных чисел, записанных в десятичной системе счисления.

1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находилось друг под другом.

2. Складывают единицы первого разряда. Если сумма меньше десяти записывают ее в разряд единиц ответа и переходят к следующему разряду (десятков).

3. Если сумма единиц больше или равна десяти, то представляют ее в виде а_о + b_о= 1·10 + с₀, где с₀- однозначное число; записывают с0 в разряд единиц ответа и прибавляют 1 к десяткам первого слагаемого, после чего переходят к разряду десятков.

4. Повторяют те же действия с десятками, потом с сотнями и т.д. Процесс заканчивается, когда оказываются сложенными цифры старших разрядов. При этом, если их сумма больше или равна десяти, то приписываем впереди обоих слагаемых нули, увеличиваем нуль перед первым слагаемым на 1 и выполняем сложение 1+0 = 1.

Заметим, что в этом алгоритме (как и в некоторых других) для краткости употребляется термин «цифра» вместо «однозначное число, изображаемое цифрой».

Алгоритм вычитания

Вычитание однозначного числа b из однозначного или двузначного числа а, не превышающего 18, сводится к поиску такого числа с, что b + с = а, и происходит с учетом таблицы сложения однозначных чисел.

Если же числа а и b многозначные и b < а, то смысл действия вычитания остается тем же, что и для вычитания в пределах 20, но техника нахождения разности становится иной: разность многозначных чисел чаще всего находят, производя вычисления столбиком, по определенному алгоритму. Выясним, каким образом возникает этот алгоритм, какие теоретические факты лежат в его основе.

Рассмотрим разность чисел 485 и 231. Воспользуемся правилом записи чисел в десятичной системе счисления и представим данную разность в таком виде: 485 - 231 = (4 · 10² + 8 · 10 + 5) - (2 · 10² + 3 · 10 + 1). Чтобы вычесть из числа 4 · 10² + 8 · 10 + 5 сумму 2 · 10² + 3 · 10 + 1, достаточно вычесть из него каждое слагаемое этой суммы одно за другим, и тогда:

(4 · 10² + 8 · 10 + 5) - (2 · 10² + 3 · 10 + 1) = (4 · 10² + 8 · 10 + 5)-2 · 10²-3 · 10-1.

Чтобы вычесть число из суммы, достаточно вычесть его из какого-либо одного слагаемого (большего или равного этому числу). Поэтому число 2 · 10² вычтем из слагаемого 4 · 10², число 3 · 10 - из слагаемого 8 · 10, а число 1 - из слагаемого 5, тогда: (4 · 10² + 8 · 10 + 5)-2 · 10²-3 · 10-1 = (4 · 10² - 2 · 10²) + (8 · 10 - 3 · 10) + (5 - 1).

Воспользуемся дистрибутивностью умножения относительно вычитания и вынесем за скобки 10² и 10. Тогда выражение будет иметь вид: (4 - 2) · 10² + (8 - 3) · 10 + (5 - 1). Видим, что вычитание трехзначного числа 231 из трехзначного числа 485 свелось к вычитанию однозначных чисел, изображенных цифрами соответствующих разрядов в записи заданных трехзначных чисел. Разности 4-2, 8 - 3 и 5- 1 находим по таблице сложения и получаем выражение: 2 · 10² + 5 · 10 + 4, которое является записью числа 254 в десятичной системе счисления. Таким образом, 485 -231 = 254. Выражение (4 - 2) · 10² + (8 - 3) · 10 + (5 - 1) задает правило вычитания, которое обычно выполняется столбиком:

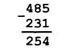
Видим, что вычитание многозначного числа из многозначного основывается на:

- способе записи числа в десятичной системе счисления;

- правилах вычитания числа из суммы и суммы из числа;

- свойстве дистрибутивности умножения относительно вычитания;

- таблице сложения однозначных чисел.

Нетрудно убедиться в том, что если в каком-нибудь разряде уменьшаемого стоит однозначное число, меньше числа в том же разряде вычитаемого, то в основе вычитания лежат те же теоретические факты и таблица сложения однозначных чисел. Найдем, например, разность чисел 760 - 326. Воспользуемся правилом записи чисел в десятичной системе счисления и представим эту разность в таком виде:

760 - 326 = (7·10² +6·10 +0)-(3·10²+ 2·10 +6).

Поскольку из числа 0 нельзя вычесть 6, то выполнить вычитание аналогичное тому, как было сделано в первом случае, невозможно. Поэтому возьмем из числа 760 один десяток и представим его в виде 10 единиц - десятичная система счисления позволяет это сделать - тогда будем иметь выражение: (7·10² + 5·10 + 10) - (3·10² + 2·10 + 6). Если теперь воспользоваться правилами вычитания суммы из числа и числа из суммы, а также дистрибутивностью умножения относительно вычитания, то получим выражение (7 - 3) ·10² + (5 - 2) ·10 + (10 - 6) или 4·10² + 3·10 +4. Последняя сумма есть запись числа 434 в десятичной системе счисления. Значит, 760 - 326 = 434.

Рассмотрим процесс вычитания многозначного числа из многозначного в общем виде.

Пусть даны два числа х = a_n·10ⁿ+ a_n-1·10^n-1+... + а₀ и

у = b_n·10ⁿ+b_n-1·10^n-1+…+b₀.

Известно также, что у < х. Используя правила вычитания числа из суммы и суммы из числа, дистрибутивность умножения относительно вычитания, можно записать, что х-у = (a_n-b_n) · 10ⁿ+ (a_n-1-b_n-1) ·10^n-1+…+(а₀-b₀) (1)

Эта формула задает алгоритм вычитания, но при условии, что для всех k выполняется условие а_k ≥ b_к. Если же это условие не выполняется, то берем наименьшее k, для которого а_к< b_к. Пусть m - наименьший индекс, такой, что m > k и а_m ≠0, а_am-1=…= а_k+1 = 0. Имеет место равенство а_m · 10^m = (а_m- 1) ·10^m + 9·10^m-1 +... + 9·10^k+1+10·10^k (например, если m = 4, k = 1, а_m = 6, то 6·10⁴= 5·10⁴ + 9·10³ + 9·10² + 10·10). Поэтому в равенстве (1) выражение (а_m- b_m) · 10^m +... + (а_к - b_к) · 10^k можно заменить на (а_m - b_m - 1)- 10^m + (9 - b_m-1) · 10^m-1 +... +(9- b_к+1) · 10^k+1+(а_k +10- b_к) · 10^k. Из того, что а_к< b_к < 10, вытекает неравенство 0 < 10 + а_к - b_к < 10, а из того, что 0 ≤ b_s ≤ 9, вытекает неравенство 0 ≤ 9-b_s < 10, где k +1 ≤ s ≤ m- 1. Поэтому в записи х-у = (a_n- b_n) · 10ⁿ+... + (а_m - b_m - 1) ·10^m +(9- b_m-1)·10^m-1 +... + (9- b_к+1) · 10^k+1 + (а_k + 10- b_к) · 10^k+…+(9- b_m-1)) · 10^m-1 +…+(9- b_к+1)все коэффициенты с индексом, меньшим m, неотрицательны и не превосходят 9. Применяя далее те же преобразования к коэффициентам a_n - b_n,…, а_m - b_m -1,через n шагов придем к записи разности х-у в виде х-у = с_n - 10ⁿ+с^n-1+... + с₀, где для всех k выполняется неравенство 0 < с_к < 10. Если при этом окажется, что с_n = 0, то надо отбросить первые слагаемые, вплоть до первого коэффициента, отличного от нуля.

Описанный процесс позволяет сформулировать в общем виде алгоритм вычитания чисел в десятичной системе счисления.

1. Записываем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.

2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, вычитаем ее из цифры уменьшаемого, записываем разность в разряд единиц искомого числа, после чего переходим к следующему разряду.

3. Если же цифра единиц вычитаемого больше единиц уменьшаемого, т.е. b₀> а₀, а цифра десятков уменьшаемого отлична от нуля, то уменьшаем цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитаем из числа 10 + а₀ число b₀ и записываем разность в разряде единиц искомого числа, далее переходим к следующему разряду.

4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, стоящие в разряде десятков, сотен и т.д. уменьшаемого, равны нулю, то берем первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшаем ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличиваем на 9, а цифру в разряде единиц на 10: вычитаем b₀ из 10 + а₀, записываем разность в разряде единиц искомого числа и переходим к следующему разряду.

5. В следующем разряде повторяем описанный процесс.

6. Вычитание заканчивается, когда производится вычитание из старшего разряда уменьшаемого.

Алгоритм умножения

Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую таблицу, называемую таблицей умножения однозначных чисел, и запоминают.

Естественно, что смысл умножения сохраняется и для многозначных чисел, но меняется техника вычислений. Произведение многозначных чисел, как правило, находят, выполняя умножение столбиком, по определенному алгоритму. Выясним, каким образом возникает этот алгоритм, какие теоретические факты лежат в его основе.

Умножим, например, столбиком 428 на 263.

Видим, что для получения ответа нам пришлось умножить 428 на 3, 6 и 2, т.е. умножить многозначное число на однозначное; но, умножив на 6, результат записали по-особому, поместив единицы числа 2568 под десятками числа 1284, так как умножали на 60 и получили число 25680, но нуль в конце записи опустили. Слагаемое 856 - это результат умножения на 2 сотни, т.е. число 85600. Кроме того, нам пришлось найти сумму многозначных чисел.

Итак, чтобы выполнять умножение многозначного числа на многозначное, необходимо уметь:

- умножать многозначное число на однозначное и на степень десяти;

- складывать многозначные числа.

Сначала рассмотрим умножение многозначного числа на однозначное. Умножим, например, 428 на 3. Согласно правилу записи чисел в десятичной системе счисления 428 можно представить в виде 4·10² + 2·10 + 8 и тогда 428·3 = (4·10² + 2·10 + 8) ·3. На основании дистрибутивности умножения относительно сложения раскроем скобки: (4·10²) ·3 + (2·10) ·3 + 8·3. Произведения в скобках могут быть найдены по таблице умножения однозначных чисел: 12·10² + 6·10 + 24. Видим, что умножение многозначного числа на однозначное свелось к умножению однозначных чисел. Но чтобы получить окончательный результат, надо преобразовать выражение 12·10² +6·10 + 24 — коэффициенты перед степенями 10 должны быть меньше 10. Для этого представим число 12 в виде 1·10 + 2, а число 24 в виде 2·10 + 4. Затем в выражении (1·10 + 2) ·10² +

+ 6·10 + (2·10 + 4) раскроем скобки: 1·10³ + 2·10²+6·10 + 2·10 + 4. На основании ассоциативности сложения и дистрибутивности умножения относительно сложения сгруппируем слагаемые 6·10 и 2·10 и вынесем 10 за скобки: 1·10³ + 2·10² + (6 + 2) ·10 + 4. Сумма 6 + 2 есть сумма однозначных чисел и может быть найдена по таблице сложения: 1·10³ + 2·10² + 8·10+4. Полученное выражение есть десятичная запись числа 1284, т.е. 428·3 = 1284.

Таким образом, умножение многозначного числа на однозначное основывается на:

- записи чисел в десятичной системе счисления;

- свойствах сложения и умножения;

- таблицах сложения и умножения однозначных чисел.

Выведем правило умножения многозначного числа на однозначное в общем виде. Пусть требуется умножить х =a_n·10ⁿ+ a_n-1·10^n-1+... + а₀ на однозначное число у:

х·у = (a_n·10ⁿ+ a_n-1·10^n-1+... + а₀) ·у = (a_n·у) ·10ⁿ+(a_n-1·у) ·10^n-1+... + а_о·у,

причем преобразования выполнены на основании свойств умножения. После этого, используя таблицу умножения, заменяем все произведения а_к·у, где 0≤k≤n, соответствующими значениями а_к·у = b_к ·10 + с и получаем: х · у = (b_n · 10+ с_n) · 10ⁿ + (b_n-1 · 10+ с_n-1) · 10^n-1 +... +(b₁ ·10+ с₁) · 10 + (b₀ ·10+ с₀) = b_n·10ⁿ⁺¹ +(с_n+ b_n-1) · 10ⁿ + … + (с₁+ b₀) · 10 +с₀. По таблице сложения заменяем суммы с_к + b_к-1, где 0 ≤ k ≤ n и k = 0, 1,2,..., n, их значениями. Если, например, с₀ однозначно, то последняя цифра произведения равна m, а к скобке (с₁+ b₀) надо прибавить 1. Продолжая этот процесс, получим десятичную запись числа х · у.

Описанный процесс позволяет сформулировать в общем виде алгоритм умножения многозначного числа на однозначное число у.

1. Записываем второе число под первым.

2. Умножаем цифры разряда единиц числа х на число у. Если произведение меньше 10, его записываем в разряд единиц ответа и переходим к следующему разряду (десятков).

3. Если произведение цифр единиц числа х на число у больше или равно 10, то представляем его в виде 10q₁ + с₀, где с₀ - однозначное число; записываем с₀ в разряд единиц ответа и запоминаем q₁ - перенос в следующий разряд.

4. Умножаем цифры разряда десятков на число у, прибавляем к полученному произведению число q, и повторяем процесс, описанный в пп. 2 и 3.

5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда.

Как известно, умножение числа х на число вида 10^k сводится к приписыванию к десятичной записи данного числа k нулей. Покажем это. Умножим число х = a_n·10ⁿ + a_n-1·10^n-1+...+ а₀ на 10^k:(a_n·10ⁿ+ a_n-1·10^n-1+...+ а₀)·10^k = а_n ·10^{n+ k}+ a_n-1·10^{n+ k-1}+…+ a₀·10^k. Полученное выражение является суммой разрядных слагаемых числа, 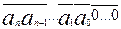, так как равно a_n·10^{n+ k}+ a_n-1 ·10^{n+ k-1}+…+a₀·10^k+0·10^k-1+0·10^k-2 +…+0·10+0. Например, 347·10³ = (3·10² +4·10 + 7) ·10³ = 3·10⁵ + 4·10⁴ + 7·10³ = 3·10⁵+ 4·10⁴ + 7·10³ + 0·10²+ 0·10 + 0 = 347000.

Заметим еще, что умножение на число у·10^k , где у - однозначное число, сводится к умножению на однозначное число у и на число 10^k. Например, 52·300 = 52· (3·10²) = (52·3) ·10² = 156·10² =15600.

Рассмотрим теперь алгоритм умножения многозначного числа на многозначное. Обратимся сначала к примеру, с которого начинали, т.е. к произведению 428·263. Представим число 263 в виде суммы 2·10² + 6·10 + 3 и запишем произведение 428· (2·10² + 6·10 + 3). Оно, согласно дистрибутивности умножения относительно сложения, равно 428· (2·10²) + 428· (6·10) + 428·3. Отсюда, применив ассоциативное свойство умножения, получим: (428·2) ·10² + (428·6) ·10 + 428·3. Видим, что умножение многозначного числа 428 на многозначное число 263 свелось к умножению многозначного числа 428 на однозначные числа 2,6 и 3, а также на степени 10.

Рассмотрим умножение многозначного числа на многозначное в общем виде. Пусть х и у- многозначные числа, причем у =b_m·10^m+b_m-1·10^m-1+…+b₀. В силу дистрибутивности умножения относительно сложения, а также ассоциативности умножения можно записать: х·у =х· (b_m·10^m+b_m-1·10^m-1+…+b₀) = (x · b_m) ·10^m + (х · b_m-1) · 10^m-1 +... + х · b₀. Последовательно умножая число х на однозначные числа b_m, b_m-1, …, b₀, а затем на 10^m, 10^m-1,..., 1, получаем слагаемые, сумма которых равна х ·у. Приходим к алгоритму умножения числа

х= на число у = .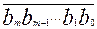

1. Записываем множитель х и под ним второй множитель у.

2. Умножаем число х на младший разряд b₀ числа у и записываем произведение х · b₀ под числом у.

3. Умножаем число х на следующий разряд b₁, числа у и записываем произведение х · b₁, но со сдвигом на один разряд влево, что соответствует умножению х · b₁, на 10.

4. Продолжаем вычисление произведений до вычисления х · b_к.

5. Полученные k + 1 произведения складываем.

Изучение алгоритма умножения многозначных чисел в начальном курсе математики, как правило, проходит в соответствии с выделенными этапами. Различия имеются только в записи. Например, при обосновании случая умножения многозначного числа на однозначное пишут: 428 ·3 = (400 + 20 + 8) ·3 = = 400 ·3 + 20 ·3 + 8 ·3 = 1200 + 60 + 24 = 1284. Основой выполненных преобразований являются:

- представление первого множителя в виде суммы разрядных слагаемых (т.е. запись числа в десятичной системе счисления);

- правило умножения суммы на число (или дистрибутивность умножения относительно сложения);

- умножение «круглых» (т.е. оканчивающихся нулями) чисел на однозначное число, что сводится к умножению однозначных чисел.

Алгоритм деления

Когда речь идет о технике деления чисел, то этот процесс рассматривают как действие деления с остатком: разделить целое неотрицательное число а на натуральное число b - это значит найти такие целые неотрицательные числа q и r, что а = bq + r, причем 0 ≤ r < b.

Выясним сначала, как осуществляется деление на однозначное число. Если на однозначное число делят однозначное или двузначное (не превышающее 89), то используется таблица умножения однозначных чисел. Например, частным чисел 54 и 9 будет число 6, так как 9·6 = 54. Если же надо разделить 51 на 9, то находят ближайшее к нему меньшее число, которое делится на 9 - это число 45, и, следовательно, неполным частным при делении 51 на 9 будет число 5. Чтобы найти остаток, надо из 51 вычесть 45:51 - 45 = 6. Таким образом 51 =9·5 + 6, т.е. при делении 51 на 9 получается неполное частное 5 и остаток, равный 6. Записать это можно иначе, при помощи деления уголком:

Будем теперь делить трехзначное число на однозначное, например, 378 на 4. Разделить 378 на 4 - это значит найти такое неполное частное q и остаток r, что 378 = 4q + г, причем остаток г должен удовлетворять условию 0 ≤ r < b, а неполное частное q - условию 4q ≤378 < 4(q + 1).

Определим, сколько цифр будет содержаться в записи числа q. Однозначным число q быть не может, так как тогда произведение 4q может быть максимально равно 36 и, значит, не будут выполняться условия, сформулированные выше для r и q. Если число q двузначное, т.е. если 10 < q < 100, то тогда 40 < 4q < 400 и, следовательно, 40 < 378 < 400, что верно. Значит, частное чисел 378 и 4 - число двузначное.

Чтобы найти цифру десятков частного, умножим последовательно делитель 4 на 20, 30, 40 и т.д. Поскольку 4·90 = 360, а 4·100 = 400, и 360 < 378 < 400, то неполное частное заключено между числами 90 и 100, т.е. q =90 + q₀. Но тогда должны выполняться неравенства: 4· (90 + q₀) ≤378 < 4· (90q + q₀ + 1), откуда 360 + 4q₀ ≤ 378 < 360 + 4(q₀+ 1) и 4q₀< ≤ 18<4(q₀+ 1). Число q₀ (цифра единиц частного), удовлетворяющее последнему неравенству, можно найти подбором, воспользовавшись таблицей умножения. Получаем, что q₀=4 и, следовательно,

неполное частное q = 90 + 4 = 94. Остаток находится вычитанием: 378 - 4·94 = 2.

Итак, при делении числа 378 на 4 получается неполное частное 94 и остаток 2: 378 - 4 · 94 + 2.

Описанный процесс является основой деления уголком:

Аналогично выполняется деление многозначного числа на многозначное. Разделим, например, 4316 на 52. Выполнить это деление - значит найти такие целые неотрицательные числа q и r, что 4316 = 52q + r, 0 ≤r < 52, а неполное частное должно удовлетворять неравенству 52q ≤4316 < 52(q + 1).

Определим число цифр в частном q. Очевидно, частное заключено между числами 10 и 100 (т.е. q - двузначное число), так как 520 < 4316 < 5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52·80 = 4160, а 52·90 = 4680 и 4160 < 4316 < 4680, то неполное частное заключено между числами 80 и 90, т.е. q = 80 + q₀. Но тогда должны выполняться неравенства:

52· (80 + q₀) ≤ 4316 < 52· (80 + q₀ + 1),

4160 + 52q₀ ≤ 4316 < 4160 + 52· (q₀ + 1),

52q₀≤156<52· (q₀+ 1).

Число q₀ (цифру единиц частного), удовлетворяющее последнему неравенству, можно найти подбором: 156 = 52·3, т.е. имеем случай, когда остаток равен 0. Следовательно, при делении 4316 на 52 получается частное 83.

Приведенные рассуждения лежат в основе деления уголком:

Обобщением различных случаев деления целого неотрицательного числа а на натуральное число b является следующий алгоритм деления уголком.

1. Если а = b, то частное q = 1, остаток r = 0.

2. Если а > b и число разрядов в числах а и b одинаково, то частное q находим перебором, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9, так как а < 10b. Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел а и b.

3. Если а > b и число разрядов в числе а больше, чем в числе b, то записываем делимое а и справа от него делитель b, который отделяем от а уголком и ведем поиск частного и остатка в такой последовательности:

а) Выделяем в числе а столько старших разрядов, сколько разрядов в числе b или, если необходимо, на один разряд больше, но так, чтобы они образовывали число d₁, больше или равное b. Перебором находим частное q₁ чисел d₁ и b, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9. Записываем q₁ под уголком (ниже b).

б) Умножаем b на q₁ и записываем произведение под числом а так, чтобы младший разряд числа bq₁ был написан под младшим разрядом выделенного числа d₁.

в) Проводим черту под bq₁ и находим разность r₁=d₁- bq₁.

г) Записываем разность r₁ под числом bq₁, приписываем справа к r₁ старший разряд из неиспользованных разрядов делимого а и сравниваем полученное число d₂ с числом b.

д) Если полученное число d₂ больше или равно b, то относительно него поступаем согласно п. 1 или п. 2. Частное q₂ записываем после q₁.

е) Если полученное число d₂ меньше b, то приписываем еще столько следующих разрядов, сколько необходимо, чтобы получить первое число d₃, большее или равное b. В этом случае записываем после q, такое же число нулей. Затем относительно d₃ поступаем согласно пп. 1, 2. Частное q₂ записываем после нулей. Если при использовании младшего разряда числа а окажется, что d₁ < b, то тогда частное чисел d₃ и b равно нулю, и этот нуль записывается последним разрядом к частному, а остаток r = d₃.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: