Заполнение квантовых состояний в зависимости от температуры.

Основные положения зонной теории.Расщепление уровней.

ЗОННАЯ ТЕОРИЯ - один из осн. разделов квант.теории тт. 3. т. описывает движ. эл-нов в кристаллах и явл-ся основой совр. теории металлов, полупроводников и диэлектриков. Из-за близкого расположения атомов в кристаллах происходит перекрытие волновых ф-ций эл-нов соседних атомов или молекул. В рез-те из кажд. дискретного энергетич. уровня атома или молекулы обр-ся энергетич. зона и электроны, находящиеся на этих уровнях, приобретают способность свободно переем-ся по кристаллу. Самая высоко располож. из полностью заполн. зон – валентная зона.Следующ. зона,располож. выше валентной,наз-ся зоной проводимости(она может быть частично заполнена или полн. свободна).Энергетич. интервал между вал. зоной и зоной пр-ти наз-ся запрещ. зоной(в эт. обл. энергий отсутств. разреш. квант. состояния).

В основе зонной теории лежат следующие главные приближения:1.Твердое тело представляет собой идеально периодический кристалл.2.Равновесные положения узлов кристаллической решетки фиксированы, то есть ядра атомов считаются неподвижными (адиабатическое приближение). Малые колебания атомов вокруг равновесных положений, которые могут быть описаны как фононы, вводятся впоследствии как возмущение электронного энергетического спектра.

3.Многоэлектронная задача сводится к одноэлектронной: воздействие на данный электрон всех остальных описывается некоторым усредненным периодическим полем.

Зонная теория является основой современной теории твёрдых тел. Она позволила понять природу и объяснить важнейшие свойства проводников, полупроводников и диэлектриков. Величина запрещённой зоны между зонами валентности и проводимости является ключевой величиной в зонной теории, она определяет оптические и электрические свойства материала. Переход электрона из валентной зоны в зону проводимости называют процессом генерации носителей заряда (отрицательного — электрона, и положительного — дырки), обратный переход — процессом рекомбинации.

Заполнение квантовых состояний в зависимости от температуры.

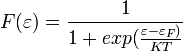Вероятность того, что электрон будет находиться в квантовом состоянии с энергией , определяется распределением Ферми-Дирака: ,где ε-энергия эл-на;ε_F-эн. ур.Ферми;K-пост. Больцмана;T-абс. темп-ра;F(ε)-вероятность заполн. уровня с эн.ε.

Для крист.,у кот. зона провод. част. заполнена,ур. Ферми навх-ся в з. пров-ти,а эн. Ферми =макс. энергии,кот. может обладать эл-он при абс. нуле темп-ры.Для крист. со своб. зоной пров-ти ур. с эн. Ферми нах-ся посередине запрещ. зоны. При абсолютном нуле из вида функции следует, что F(ε) = 1 при ε < ε_F;F(ε) = 0 при ε >ε_F.То есть все состояния, лежащие ниже ур. Ферми, полностью заняты эл-нами, а выше него свободны. При темп-ре выше абс.нуля знач. ф-ии отлич. от 0 и 1 в некот. узк. окр-ти ур. Ферми. Это означ.,что часть эл-ов,у кот. ε < ε_F за счёт эн. тепл. дв-ия ат. перех. на квант. уровни с эн.,кот. больше эн.Ферми.По эт. же прич. и для крист., у кот. ур. Ф. нах-ся посередине запрещ. з.,сущ. вер-ть перехода эл-ов из сост вблизи потолка вал. зоны в сост. вблизи дна зоны проводимости.Вер-ть реализации так. перехода зав. от ширины запр. з. и темп-ры кристалла. 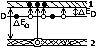42.Электрическая проводимость с позиции зонной теории. С т.зр. зонной теории крист. подразделяются на проводники(металлы), у кот. в зоне пр-ти при Т=0 им-ся эл-ны,и диэлектрики,у кот. в эт. зоне эл-ов нет.Всвою очередь диэлектрики в зав-ти от ширины запрещ. зоны условно подразд. на собственно диэлектрики,у кот шир. запр. з. ∆ε≥3-5Эв,и пп,у кот. ∆ε~1-3Эв.В связи с этим в пп ок-ся возможн. переброс эл-ов из вал. з. в з. пр-ти за счёт тепл. возбуждения при Т≠0 или друг. внешн. воздействия,способность передать эл-нам эн. больше 1эВ. Т.о. пр-ки отлич. от диэл-ов не тем,что в пр-ках есть эл-ны,кот. мог. своб. дв-ся,а в д-ках их нет,а тем,что из-за разн. хар-ра заполн. зон в перв. случ возможно перераспределение импульсов эл-ов,что и обеспечивает эл.пр-ть пров-ов,во втором же случ. это перераспределение невозможно без внешн. возд-ия из-за налич. достаточно шир. запрещ. энергетич. зоны. 43.Собственные и примесные полупроводники. Удельная проводимость: δ=10^-5÷10^.-8Ом*м.К ПП относятся: C,Si, Ge, Te, Sn, S. Различ. 2 вида пп: собственные,примесные. 1.собственные ПП. Проводимость химически чистых ПП называется собственной, а сами ПП наз-ся собственными ПП(ведут себя как диэлектрики).При повыш. темп-ры или за счёт др. внешн. возд-ия часть эл-ов с верхн. ур. вал. з. мож. быть переброшена на нижн. ур. зоны пров-ти.Следует отметить,сто не только эл-ны,перешедшие в зону пров-ти, обуславливают эл. пров-ть собств. пп.В рез-те перехода части эл-ов из вал. в з. пров-ти соотв-ие места в вал. зоне освобожд. и обр. «дырки».Благодаря им эл-ны в вал. зоне могут перераспр. свои импульсы в пределах, соотв-их эн. вал. зоны→появл-ся эл. ток.Дырки перераспределяются и вед. себя как полож. заряж. ч-цы.Возникающ. в рез-те движ. дырок проводимость наз-ся «дырочной». 2.Примесные ПП. Проводимость ПП в большой степени зависит от чистоты ПП => от наличия примесей в ПП. Проводимость ПП, обусловленная примесями называется примесной, а сами ПП называются примесными ПП.По своей природе примеси могут быть или доп. поставщиками эл-нов в кр.- донорами, или акцепторами. Энергетич. уровни лишних эл-ов нах-ся вблизи дна зоны пров-ти.Они наз-ся донорными. В рез-те перехода эл-ов с дон. ур. в зону пр-ти возн. электр. примесн. пров-ть,кот. наз-ся проводимостью n-типа.

Эн. уровни примесей,на кот. могут переходить эл-ны,наз-ся акцепторными уровнями. Они обр-ся в запр. зоне и располаг. вблизи верхн. границы валентн. зоны.Электроны из вал. з. могут легко перех. на прим. акцепторн. ур.→возник. дырочн. прим. пр-ть. Дырочн. прим. пр-ть пп наз-ся проводимостью р-типа.

44.Динамика электронов в кристаллической решётке полупроводников. Для опис. движ. заряж. ч-ц – эл-нов и дырок под действием внешн. полей, ч-цам следует приписать не только заряд, но и динамическую хар-ку – массу, которая не совпадает с массой своб. эл-на и носит название «эффективной массы» m^*. Причина введения вместо массы ч-цы – эффективной массы заключ. в том, что помимо внешних полей на заряж. ч-цы действуют внутрикристаллич. поля, создаваемые ионами, расположенными в узлах кристаллич. р-ки. .m_e^*=ћ²/(d²ε/dk²) –эффективная масса электрона в кристалле. m^* _дырки=-m^*_e, q_дырки=+e → Дырки можно рассм-ть как полож. заряды с полож. эф. массой→дырочн. пр-ть в верхн. части вал. зоны мож. опис-ся так же, как эл. пр-ть вблизи дна зоны пров-ти.Отметим также, что эффективная масса дырок обычно превышает эффективную массу электронов, т.к. величина интегралов перекрытия для более высоко расположенной зоны проводимости больше, чем для валентной зоны.