 |
Порядок выполнения работы.
|
|
|
|
Виртуальная лабораторная работа №21
“ Определение логарифмического декремента и
коэффициента затухания ”
Целью работы является изучение затухающих периодических колебаний и вычисление его математических параметров.
Введение. Рассмотрим затухающие колебания на примере горизонтальных колебаний твердого тела массы m, связанного со стенкой пружиной жесткостью k, масса которой mпр << m (Рис.1). Трением между телом и полом будем пренебрегать (ктр =0). Сила сопротивления движению тела со стороны внешней среды F c = -r V, где r – коэффициент сопротивления, а V – скорость тела. Будем решать задачу в случае движения тела вдоль оси Х.
Второй закон Ньютона в нашем случае при скорости тела V << c можно записать в виде
. (1)
В проекциях на оси Х и Y из (1) очевидно следуют уравнения:
→ 
- kx – rVx = m ax, (2)
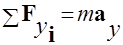→ N – mg = 0. (3)
Из (3) вытекает равенство N = mg. Из (2), поделив на m, с учетом, что
, окончательно получим дифференциальное уравнение в канонической форме
, (4)
где 2β= r/m; ω02=k/m.
Будем искать решение уравнения (4) в виде («подстановка Эйлера»)
. (5)
Подставляя (5) в (4) получим
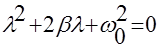. (6)
Частными решениями квадратного уравнения (6) являются значения:
. (7)
Рассмотрим чаще всего встречающийся случай, когда затухание мало (
<< 
). В этом случае решение (7)- числа комплексные:
, (8)
где 
(«мнимая единица»).
Общим решением уравнения (4) является линейная комбинация частных решений:
, (9)
где С1 и С2 комплексные коэффициенты, которые можно найти, принимая во внимание, что искомое x- принципиальновещественное число. То есть всегда должно выполняться равенство x = x*, где x* - число, комплексно сопряженное числу x (Числом, комплексно сопряженным комплексному числу z = a + ib, называется комплексное число z = a – ib, где а и b- числа вещественные).Поэтому можно написать:
|
|
|
. (10)
Подставляя в (10) значения λ1 и λ2 из (8), получим, что (10) верно, если выполняются соотношения:
. (11)
Из (11) следует, что
; 
. (12)
Подставляя (12) в (9), с учетом (8) и «формулы Эйлера»
, получим решение уравнения (4) в окончательном виде
(13)
где 
. (14)
График зависимости смещения от времени (2) показан на рис. 1 в виде зависимости х(t).
Рис.1
А1, А2, А3 – амплитуды колебания, отличающиеся по времени равному периоду. Период затухающего гармонического колебания можно определить как:
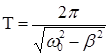(15)
Напомним, что периодом колебания называется время за которое совершается одно полное колебание.
Если рассматривать отношение амплитуд, отличающихся моментом времени равным периоду, то можно говорить еще об одной величине, характеризующей затухающее колебание, это декремент затухания:
(16)
Логарифм этого отношения называют логарифмическим декрементом затухания:
(17)
где i = 1, 2, 3, … т.е. номер амплитуды.
Учитывая (16), для расчета величины λ получим
, (18)
где β – коэффициент затухания, T – период затухающего колебания, а для
для коэффициента затухания β формулу:
(19)
Уравнение, аналогичное (4), получается при рассмотрении электрических колебаний тока I в колебательном контуре, включающем последовательно соединенные конденсатор емкостью С, индуктивность L и сопротивление R:
,
где 
, а 
.
Очевидно, что в этом случае все выводы, сделанные при рассмотрении механических колебаний, правомочны и при описании затухающих колебаний тока в колебательном контуре.
Описание модели работы.
Данная лабораторная работа смоделирована на компьютере, программное обеспечение которого, каждый раз при запуске программы строит на экране монитора график функции (13). При каждом запуске программы период затухающих колебаний устанавливается случайным образом, поэтому для каждого работающего студента он будет всегда разным. Обращаем Ваше внимание на то что, управление программой очень простое и требуется только перемещать курсор мышки по экрану, нажимая левую клавишу мышки. Вы можете самостоятельно устанавливать значение коэффициента затухания движком ползунка, который увидите на экране монитора, и изменение формы кривой колебательного процесса сразу же отреагирует на это. Амплитудные значения измеряются положением курсора мышки в миллиметрах.
|
|
|
Ось t имеет размерную оцифровку, позволяющую определить период колебания. Если определить число колебаний N совершающихся за время t, то период затухающего колебания можно определить как:
(20)
Порядок выполнения работы.
Целью работы является вычисление величины логарифмического декремента затухания λ и коэффициента затухания β по измерениям амплитуд затухающего колебания и периода.
1. Найдите на рабочем столе компьютера значок “Работа №21” и щелкните по нему двойным щелчком мышки. На экране монитора на голубом фоне появится график колебания в котором Вы можете изменять коэффициент затухания. Установите курсор на движок “коэффициент затухания” и, нажав левую клавишу мышки, переместите движок в любое положение, тем самым Вы установите какое то значение β, которое изменять при измерениях уже нельзя.
2. Вначале определите период затухающего колебания. Для этого подсчитайте, за какое время (по шкале времени t) совершается N полных колебаний и по формуле (20) определите Т, записав его значение в таблицу измерений. Число колебаний N выберете сами в пределах 6-12 колебаний.
3. Подведите курсор к точке, где первая амплитуда максимальна и нажмите левую клавишу мышки. На экране появится значение амплитуды, которое необходимо записать в таблицу измерений.
4. Проведите такие же измерения для соседних 6-7 амплитуд, заполнив таблицу. Подпишите результаты измерений у преподавателя.
5. По формулам (17) и (19) рассчитайте значения li, βi и запишите их в таблицу измерений.
6. Вычислите абсолютную доверительную погрешность логарифмического декремента затухания и коэффициента затухания по алгоритму прямых многократных измерений, заполняя постепенно таблицу измерений.
|
|
|
7. Округлите доверительную погрешность и результат по правилам округления, записав результат в установленной форме.
Таблица измерений
=
| №п/п | Аi | λi | βi | ∆λi | (∆λi)2 | ∆βi | (∆βi)2 |
| …. | |||||||
λср = βср =
∑(∆λi)2 = ∑((∆βi)2 =
∆λ = ∆β =
Отчет по лабораторной работе должен содержать: подписанные преподавателем измерения, заполненную таблицу измерений и вычисленные значения логарифмического декремента затухания и коэффициента затухания с погрешностями ∆λ и ∆β.
Контрольные вопросы для получения допуска.
1. Дайте определение затухающего колебания и напишите его уравнение.
2. Дайте определения параметров колебательного движения.
3. Нарисуйте график затухающего колебания.
4. Что характеризует коэффициент затухания?
Список литературы
1. И.В.Савельев. Курс общей физики. т.N2. М. 1986
2. Конспект прочитанных лекций.
Составители: доц. С.П. Майбуров
профессор П.Г. Шляхтенко
|
|
|
