 |
Решение задачи коммивояжера при помощи надстройки MS Excel «Поиск решения»
|
|
|
|
Метод полного перебора
Мощным средством анализа данных MS Excel является надстройка «Поиск решения». С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки, данные которых, определяют значение целевой ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.
Программа Поиск решений – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации, используется с 1991 года.
Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями: количество неизвестных (decision variable) – 200; количество формульных ограничений (explicit constraint) на неизвестные – 100; количество предельных условий (simple constraint) на неизвестные – 400.
Постановка задачи коммивояжера, которую необходимо решить посредством надстройки «Поиск решения» методом полного перебора следующая:
«Сотруднику компании ООО «Новые технологии» Петрову Н.И. необходимо обновить программный продукт автоматизированного учета в пяти организациях: А, Б, В, Г и Д. Он решил начать свой обход с организации «А», так как она находится на первом этаже дома, в котором проживает Петров. Сотруднику необходимо, спланировать свой маршрут таким образом, чтобы к концу рабочего дня обойти все организации в определенном порядке и выполнив свою работу, вернутся домой (в пункт «А»). В каком порядке Петрову следует обходить организации, чтобы его замкнутый тур был кратчайшим? Если расстояния между каждой парой организаций заданы следующей квадратной матрицей (5x5):
|
|
|
Решение: Разместим исходные данные на рабочем листе (рис 2.1). Заменим знак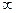 
числом 10000 (на результат решения исключение пути не оказывает влияния).
 |
Рисунок 2.1 Исходные данные задачи
Вводим формулы:
Таблица 1
| Ячейка | Формула | Примечание |
| B9 | = СУММ(B4:B8) | Распространяем на диапазон B9:F9 |
| G4 | = СУММ(B4:F4) | Распространяем на диапазон G4:G8 |
| C19 | =СУММПРОИЗВ(B4:F8;B13:F17) | Целевая функция |
| E19 | =B4+C5+D6+E7+F8 | Исключение пути |
| B23 | =$C$10-C10+4*C5 | Распространяем на диапазон B23:E23 |
| B24 | =$D$10-C10+4*C6 | Распространяем на диапазон B24:E24 |
| B25 | =$E$10-C10+4*C7 | Распространяем на диапазон B25:E25 |
| B26 | =$F$10-C10+4*C8 | Распространяем на диапазон B26:E26 |
Сценарий решения.
1. Запускаем надстройку MS Excel «Поиск решения» командой Сервис/ Поиск решения. И заполняем (рис. 2.2).
2. Для того чтобы выполнялись условия однократного посещения сотрудником организаций и в то же время запланированный Петровым маршрут был пройден полностью, введем ограничения: в строки B9, G4 заводим формулы из таблицы 1 и распространяем их на соответствующие диапазоны B9:F9 и G4:G8. Задаем следующие данные $B$9:$F$9=1 и $G$4:$G$8=1 в Ограничения окна «Поиск решения». Таким образом, мы можем отследить порядок обхода организаций сотрудником, оценить правильность выбора и оптимальность его маршрута.
3. Выбираем ячейку B19 и устанавливаем ее адрес в Целевую ячейку окна «Поиск решения», чтобы определить длину наикратчайшего маршрута. Для этого в ячейку B19 предварительно заносим соответствующую формулу из таблицы 1. Когда программа «Поиск решения» вычислит оптимальный маршрут Петрова и станет известен порядок обхода организаций (из Матрицы переменных) будут известны и расстояния между конкретными парами организаций. Затем при помощи простых математических подсчетов программа рассчитает протяженность оптимального маршрута.
|
|
|
4. Устанавливаем еще одно ограничение в окно «Поиск решения»: $E$19=0. В указанную ячейку вводим формулу из таблицы 1 и исключаем таким образом, заведомо ложный порядок движения Петрова в порядке обхода организаций.
5. В связи с тем, что ячейки диапазона B4:F8 – изменяемые, в Ограничение окна «Поиск решения» необходимо добавить строку B$4$:F$8$=двоичное.
6. Заводим в ячейки B23; B24; B25; B26 соответствующие формулы из таблицы 1 и распространяем их на следующие диапазоны: B23:E23 B24:E24; B25:E25; B26:E26 для учета всех возможных вариантов обхода организаций сотрудником и выбора из них оптимального. Формулы задаем таким образом, чтобы обеспечить исключение ложного пути, соблюдая условие задачи об обходе всех организаций по одному разу.
7. Добавляем в Ограничения окна «Поиск решения» $B$23:$E$26 ≤ 3.
 |
Рисунок 2.2 Окно «Поиск решения»
Так как это линейная модель, то необходимо фиксировать в окне Параметры поиска решений на позицию Линейная модель и Неотрицательные значения (рис. 2.3). После того, как все поля и ячейки заполнены нажимаем кнопку «Выполнить» и появляется окно диалога с описанием результатов процесса оптимизации. Чтобы отобразить найденное решение в ячейках листа, устанавливаем переключатель «Сохранить найденное решение» и нажимаем кнопку ОК. Найденная минимальная величина помещается в целевую ячейку, а переменные ячейки заполняются оптимальными значениями переменных, которые удовлетворяют установленным ограничениям.
Рисунок 2.3 Окно «Параметры поиска решения»
Таким образом, получаем следующий результат. Если Петров переходит из организации в организацию, то на рис. 2.4 в диапазоне B4:F8 мы будем наблюдать порядок его перемещений. Если видим, что в ячейке, которая отнесена к организации «В» стоит единица, значит сотрудник посетил эту организацию следующей за пунктом «А». Если в ячейке ноль – сотрудник организацию не посещал.
|
|
|
 |
Рисунок 2.4 Результаты решения задачи коммивояжера
Вывод:
В ходе анализа полученных результатов, приходим к выводу: наиболее оптимальным маршрут Петрова будет в том случае, если он начал свой путь с организации «А», посетит другие организации в следующем порядке «В», затем «Д», далее «Б» и «Г», из которой вернется к началу своего пути (в организацию «А»). представим путь схематически:
А’В’Д’Б’Г’А
Длина кратчайшего маршрута (значение целевой ячейки) в результате составит – 21.
Задача решена. Кратчайший маршрут Петрова найден.
ЗАКЛЮЧЕНИЕ
Задача коммивояжера была поставлена в 1934 году. Ее сущность заключается в поиске оптимального маршрута движения при необходимости посетить все запланированные объекты с наименьшими финансовыми и временными издержками. Как правило, речь идет о простом перемещении по заданным точкам, либо с перевозкой груза небольшого формата на транспортном средстве.
Задача коммивояжера является одной из знаменитых задач теории комбинаторики и пользуется популярностью благодаря тому, что к ней сводится большое количество практических задач.
Среди современных практических приложений задачи можно выделить: доставку продуктов в магазин со склада, работу почтальона по разноске корреспонденции, мониторинг объектов (нефтяные вышки, базовые станции сотовых операторов), изготовление отверстий на специализированном станке.
Для решения задачи коммивояжера используют различные группы простейших методов: полный и случайный перебор, жадный и деревянный алгоритмы, метод имитации отжига. Широкое применение получили различные модификации более эффективных методов, таких как метод ветвей и границ, генетических алгоритмов, а также алгоритм муравьиных колоний.
В работе была поставлена задача, сводимая к задаче коммивояжера, и составлена схема оптимального маршрута, подробно рассмотрен порядок выбора кратчайшего пути при помощи использования надстройки MS Excel «Поиск решения» методом полного перебора. Результаты решения были выведены на отдельный рабочий лист Excel.
|
|
|
Изучение особенностей задачи коммивояжера позволило сделать следующий вывод: актуальным в настоящее время остается поиск точных и приближенных способов решения этой задачи как с теоретической, так и с практической точек зрения. Более того, темпы современной жизни меняют отношение человека ко времени, сегодня пользователь не любит ждать, изыскивает возможности сократить время ожидания, найти оптимальное решение в кратчайшие сроки. Все это свидетельствует о росте в будущем потребности в эффективном решении задач коммивояжера и иных родственных им оптимизационных задач, которые позволили бы существенно сэкономить ограниченные ресурсы организаций.
Министерство образования и науки РФ
ГБОУ СПО «Шадринский политехнический колледж»
Заведующая учебной частью
____________ Блинова Н.А.
«____»______________20__г
Курсовая работа
по дисциплине «Математические методы»
на тему «Задача о коммивояжере. Метод полного перебора»
»
Студента: _________/Рудакова М.В./
Руководитель: _____________/Ханина О.В./
Шадринск, 2012 г.
|
|
|
