 |
Работы, не отвечающие перечисленным требованиям, будут возвращаться для переделки.
|
|
|
|
Механика. Теоретическая механика.
Сборник заданий для контрольных работ для студентов заочной формы обучения
Салават 2009
Предназначено для студентов заочной формы обучения специальностей: 240801 - Машины и аппараты химических производств; 140610 - Электрооборудование и электрохозяйства предприятий, организаций и учреждений.
Сборник составлен на основе широко известного сборника контрольных заданий для студентов заочников под редакцией С.М. Тарга.
Приведена в соответствие с требованиями государственного образовательного стандарта рабочая программа, переработаны методические указания и исходные данные задач.
Составитель Насибуллин Р.И., доцент кафедры
"Оборудование предприятий
нефтехимии и нефтепереработки"
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Для изучения курса необходимо иметь соответствующую математическую подготовку. Во всех разделах курса, начиная со статики, широко используется векторная алгебра. Необходимо знать основные операции с векторами: сложение векторов, разложение вектора на составляющие, проекции векторов на координатные оси, скалярное и векторное произведения двух векторов и свойства этих произведений, а так же дифференцировать векторы.
Необходимо знать дифференциальное и интегральное исчисление, уметь находить производные функций одного и нескольких переменных, вычислять неопределенные и определенные интегралы, знать методы решения дифференциальных уравнений первого и второго порядка..
При изучении материала курса по учебнику нужно прежде всего уяснить существо каждого излагаемого там вопроса. Главное – это понять изложенное в учебнике, а не "заучить".
|
|
|
Изучать материал рекомендуется по темам (пунктам приводимой ниже программы) или по главам (параграфам) учебника. Целесообразно сначала прочитать весь материал темы, затем надо вернуться к местам, вызвавшим затруднения и внимательно разобраться в том, что было неясно. Особое внимание обратите на формулировки соответствующих определений, теорем и т.п.; в точных формулировках, как правило, существенно каждое слово и очень полезно понять, почему данное положение сформулировано именно так.
Необходимо также понять ход всех доказательств, разобраться в их деталях. Доказательства надо уметь воспроизводить самостоятельно.
При изучении курса особое внимание следует уделить приобретению навыков решения задач. Для этого, изучив материал данной темы, надо сначала обязательно разобраться в решениях соответствующих задач, которые приводятся в учебнике, обратив особое внимание на методические указания по их решению.
РАБОЧАЯ ПРОГРАММА
В программе дается перечень вопросов, которые как основная часть курса должны изучаться студентами всех специальностей. Вопросы не включенные в Государственный образовательный стандарт специальности 240801 выделены мелким шрифтом, но они также рекомендуются к изучению.
Введение в теоретическую механику
Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. Объективный характер законов механики.
СТАТИКА ТВЕРДОГО ТЕЛА
Основные понятия и аксиомы статики. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, силы внешние и внутренние.
Аксиомы статики. Связи и реакции связей. Основные виды связей: гладкая плоскость или поверхность, гладкая опора, гибкая нить, цилиндрический и сферический шарниры, невесомый стержень; реакции этих связей.
|
|
|
Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое и аналитические условия равновесия системы сходящихся сил.
Равновесие произвольной системы сил. Момент силы относительно точки (центра) как вектор. Момент силы относительно оси. Пара сил; момент пары. Свойства пары сил. Понятие о приведении системы сил к заданному центру. Главный вектор и главный момент системы сил. Условия равновесия произвольной системы сил, приложенных к твердому телу. Теорема Вариньона о моменте равнодействующей.
Система сил, расположенных на плоскости (плоская система сил). Условия равновесия плоской системы сил (три формы условий равновесия). Равновесие соединенных тел.
Система параллельных сил. Условия равновесия системы параллельных сил. Центр параллельных сил и тяжести твердого тела, его координаты. Центр тяжести объема, площади и линии. Способы определения положения центров тяжести.
КИНЕМАТИКА
Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики.
Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная от ее радиуса-вектора по времени. Ускорение точки как производная от вектора скорости по времени. Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.
Естественный способ задания движения точки. Оси естественного трехгранника. Определение скорости и ускорения точки: касательное и нормальное ускорения точки.
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Поступательное и вращательное движения твердого тела. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращение твердого тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси. Вектор угловой скорости тела. (Выражение скорости точки вращающегося тела в виде векторного произведения.)
|
|
|
Плоскопараллельное (плоское) движение твердого тела. Плоское движение твердого тела и движение плоской фигуры в ее плоскости. Уравнения движения плоской фигуры. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса: независимость угловой скорости фигуры от выбора полюса. Определение скорости любой точки фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса. Теорема о проекциях скоростей двух точек фигуры (тела). Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. теорема об ускорения х точек плоской фигуры
Сложное (составное) движение точки. Абсолютное и относительное движения точки; переносное движение. Теорема о сложении скоростей. Теорема о сложении ускорений (теорема Кориолиса); кориолисово ускорение и его вычисление.
ДИНАМИКА
Введение в динамику. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Законы механики Галилея-Ньютона. Инерциальная система отсчета. Задачи динамики.
Динамика точки. Дифференциальные уравнения движения свободной и несвободной материальной точки в декартовых координатах. (Уравнения движения материальной точки в проекциях на оси естественного трехгранника.) Две основные задачи динамики для материальной точки. Решение первой задачи динамики.
Решение второй задачи динамики. Начальные условия. Постоянные интегрирования и их определение по начальным условиям. Примеры интегрирования дифференциальных уравнений движения точки в случаях силы, зависящей от времени, от положения точки и от ее скорости.
Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки; переносная и кориолисова силы инерции. Принцип относительности классической механики. Случай относительного покоя.
|
|
|
Прямолинейные колебания точки. Свободные колебания материальной точки под действием восстанавливающей силы, пропорциональной расстоянию от центра колебаний. Амплитуда, начальная фаза, частота и период колебаний. Затухающие колебания материальной точки при сопротивлении, пропорциональном скорости; период этих колебаний, декремент колебаний. Вынужденные колебания точки при гармонической возмущающей силе и сопротивлении, пропорциональном скорости. Резонанс.
Введение в динамику механической системы. Механическая система. Классификация сил, действующих на систему: силы активные (задаваемые) и реакции связей; силы внешние и внутренние. Свойства внутренних сил. Масса системы. Центр масс; радиус-вектор и координаты центра масс.
Момент инерции. Момент инерции твердого тела относительно оси; радиус инерции. Теорема о моментах инерции тела относительно параллельных осей. Примеры вычисления моментов инерции: моменты инерции однородного тонкого стержня, тонкого круглого кольца, круглого диска, сплошного круглого цилиндра.
Общие теоремы динамики
Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс.
Теорема об изменении количества движения. Количество движения материальной точки. Импульс силы. Теорема об изменении количества движения материальной точки.
Количество движения механической системы; его выражение через массу системы и скорость ее центра масс. Теорема об изменении количества движения механической системы. Закон сохранения количества движения механической системы.
Теорема об изменении момента количества движения. Момент количества движения материальной точки относительно центра и относительно оси. Главный момент количеств движения или кинетический момент механической системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.
Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Элементарная работа силы; аналитическое выражение элементарной работы. Работа силы на конечном перемещении точки. Работа силы тяжести, силы упругости, силы приложенной к вращающемуся телу. Мощность. Теорема об изменении кинетической энергии точки.
|
|
|
Кинетическая энергия механической системы. Теорема Кёнига. Кинетическая энергия твердого тела при поступательном движении, при вращении вокруг неподвижной оси и при плоскопараллельном движении тела. Теорема об изменении кинетической энергии механической системы. Понятие о потенциальном силовом поле и потенциальной энергии. закон сохранения механической энергии.
АНАЛИТИЧЕСКАЯ МЕХАНИКА
Принцип Даламбера. Сила инерции материальной точки. Принцип Даламбера для материальной точки и механической системы. Метод кинетостатики. Давление на оси вращающегося тела.
Принцип возможных перемещений и общее уравнение динамики. Возможные или виртуальные перемещения точки и механической системы. Число степеней свободы системы. Классификация связей. Идеальные связи. Принцип возможных перемещений. Общее уравнение динамики.
Уравнения Лагранжа. Обобщенные координаты системы; обобщенные скорости. Выражение элементарной работы в обобщенных координатах. Обобщенные силы и их вычисление. Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа 2-го рода.
СПИСОК ЛИТЕРАТУРЫ
Тарг С.М. Краткий курс теоретической механики. М., 1963 и последующие издания.
Мещерский И.В. Сборник задач по теоретической механике. М., 1970 и последующие издания.
Сборник заданий для курсовых работ по теоретической механике/ Под ред. А.А. Яблонского. М., 1972 и последующие годы издания.
Цывильский В.Л. Теоретическая механика: Учеб. для втузов. -М.: Высш. шк., 2001. -319 с.
Харин О.Н. Лекции по теоретической механике. Часть 1: Учебное пособие. –М.: ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004, 148 с.
Харин О.Н., Левитский Д.Н. Лекции по теоретической механике. Часть 2: Учебное пособие. –М.: ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004, 194 с.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
СОДЕРЖАНИЕ ЗАДАНИЙ, ВЫБОР ВАРИАНТОВ, ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ, ОБЩИЕ ПОЯСНЕНИЯ К ТЕКСТУ ЗАДАЧ
Студенты специальности 240801 - Машины и аппараты химических производств выполняют задачи C1, C2, K1, K2, Д1, Д2, ДЗ.
Студенты специальности 140610 - Электрооборудование и электрохозяйства предприятий, организаций и учреждений выполняют задачи C1, C2, K1, K2, КЗ Д1, Д2, ДЗ Д4, Д5.
К каждой задаче дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С1.4 – это рис. 4 к задаче C1 и т.д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4 и т.д.). Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы.
Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице — по последней; например, если шифр оканчивается числом 46, то берет рис. 4 и условия № 6 из таблицы.
Задание выполняется в тетради, на обложке указываются: название дисциплины, фамилия и инициалы студента, номер группы, номер варианта и другие необходимые данные. На
Решение каждой задачи следует начинать на развороте тетрадина четной странице, начиная со второй. В задаче следует привести исходные данные и что требуется определить. Чертеж выполняется с учетом условий решаемого варианта задачи; на нем все утлы, действующие силы, число тели их расположение на чертеже должны соответствовать этим условиям. Рисунок должен быть ясным и понятным, на рисунке следует показать вектора, размеры и другие необходимые величины, размер рисунка должен быть удобным для восприятия, в некоторых задачах, например К2, соблюдение масштаба обязательно. Решение задач необходимо сопровождать краткими пояснениями (какие формулы или теоремы применяются, откуда получаются те или иные результаты и т.п.) и подробно излагать весь ход расчетов. Следует соблюдать правила приближенных вычислений. На каждой странице следует оставлять поля для замечаний рецензента.
Работы, не отвечающие перечисленным требованиям, будут возвращаться для переделки.
ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
СТАТИКА
Задача С1
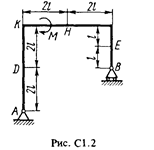
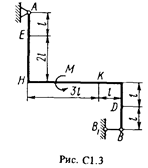
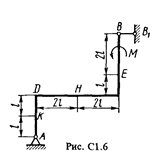
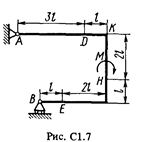
Жесткая рама (рис. С1.0 – С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню ВВ1, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.
| 
| 
| 
|
| 
| 
| 
|
| 
|
Таблица С1.
| Сила | 
| |||||||
| Номер усло-вия | F1 = 10 Н | F2 = 20 H | F3 = 30 H | F4 = 40 H | ||||
| Точка прилож | α1° | Точка прилож. | α2° | Точка прилож. | α3° | Точка прилож. | α4° | |
| – | – | D | Н | – | – | |||
| K | – | – | – | – | Е | |||
| – | – | H | K | – | – | |||
| D | – | – | – | – | E | |||
| – | – | K | E | – | – | |||
| H | – | – | D | – | – | |||
| – | – | E | – | – | K | |||
| D | – | – | H | – | – | |||
| – | – | H | – | – | D | |||
| E | – | – | – | – | K |
На раму действуют пара сил с моментом М = 50 Н·м и две силы, значения которых, направления и точки приложения указаны в таблице (например, в условиях № 1 на раму действуют сила F 1 = 10 Н под углом 60° к горизонтальной оси, приложенная в точке К, и сила F 4 = 40 Н под углом 45° к горизонтальной оси, приложенная в точке Е).
Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять l = 0,5 м.
Указания. Задача C1 – на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки А). При вычислении момента силы 
часто удобно разложить ее на составляющие 
и 
, для которых плечи легко вычисляются, в частности на составляющие, параллельные координатным осям, и воспользоваться теоремой Вариньона; тогда 
. Для проверки следует составить дополнительное уравнение равновесия, например уравнение моментов относительно другой точки, и подставить найденные значения.
Пример C1. Жесткая пластина ABCD (рис. C1) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
|
Дано: F = 25 кН, α = 60°, Р = 18 кН, γ =75°, М = 50 кН·м, β = 30°, l = 0,5 м.
Определить: реакции в точках A и B, вызываемые действующими нагрузками.
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы: силу , пару сил с моментом М, натяжение троса 
(по модулю Т = P) и реакции связей 
(реакцию неподвижной шарнирной опоры A изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу на составляющие 
(F' = F cos α, F" = F sin α) и учтем, что 
. Получим
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ: XA = – 8,5 кН, YA = – 23,3 кН, RB = – 7,3 кН. Знаки указывают на то, что силы 
и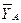 
направлены противоположно показанным на рис. С1.
Задача С2
Однородная прямоугольная плита весом Р = 10 кН со сторонами АВ = 3 l, ВС = 2 l закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС' (рис. С2.0–С2.9).
| 
| 
| 
|
| 
| 
| 
|
| 
|
| Сила | 
| |||||||
| Номер усло-вия | F1 = 5 kН | F2 = 7 kH | F3 = 9 kH | F4 = 12 kH | ||||
| Точка прилож. | α1° | Точка прилож. | α2° | Точка прилож. | α3° | Точка прилож. | α4° | |
| D | – | – | E | – | – | |||
| H | D | – | – | – | – | |||
| – | – | E | – | – | D | |||
| – | – | – | – | E | H | |||
| E | – | – | H | – | – | |||
| – | – | D | H | – | – | |||
| – | – | H | – | – | D | |||
| E | H | – | – | – | – | |||
| – | – | – | – | D | E | |||
| – | – | E | D | – |
На плиту действуют пара сил с моментом М = 8 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С2; при этом силы 
, лежат в плоскостях, параллельных плоскости ху, сила 
– в плоскости, параллельной xz, сила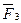 
– в плоскости, параллельной уz. Точки приложения сил (D, Е, Н) находятся в серединах сторон плиты.
Определить реакции связей в точках A, В и С. При подсчетах принять l = 0,2 м.
Указания. Задача С2 – на равновесие тела под действием пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (или подпятника) имеет три составляющие, а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира.
Пример С2. Вертикальная прямоугольная плита весом Р (рис. С2) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD', лежащим в плоскости, параллельной плоскости уz. Па плиту действуют сила 
, (в плоскости xz), сила , (параллельная оси у) и пара сил с моментом М (в плоскости плиты).
|
Дано: Р = 5 кН, М= 3 кН·м, F1 = 6 кН, F2 = 7,5 кН, α = 30°, АВ = 1м, ВС = 2 м, СЕ = 0,5 AB, ВК = 0,5 BC.
Определить: реакции опор А, В и стержня DD'.
Решение. 1. Рассмотрим равновесие плиты. На нее действуют заданные силы 
и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие 
, цилиндрического (подшипника) – на две составляющие 
(в плоскости, перпендикулярной оси подшипника), реакцию 
стержня направим вдоль стержня, предполагая, что он растянут.
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
Подставив в составленные уравнения числовые значения всех заданных величин и решив затем эти уравнения, найдем, чему равны искомые реакции.
Ответ: XA = –5,2 кН, YA = 3,8 кН, ZA = 28,4 кН, YB = –7,5 кН, ZB = –12,4 кН, N = 14,5 кН. Знаки указывают, что силы 
направлены противоположно показанным на рис. С2.
Задача К1
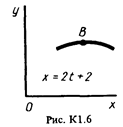
Точка В движется в плоскости ху (рис. К1.0 – К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f 1 (t), у = f 2 (t), где х и у выражены в сантиметрах, t – в секундах.
Найти уравнение траектории точки; для момента времени t 1 = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
| 
| 
| 
|
| 
| 
| 
|
| 
|
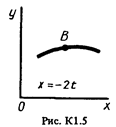
Зависимость х = f 1 (t) указана непосредственно на рисунках, а зависимость у = f 2 (t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задачах C1, C2, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 – по последней.
Таблица К1
| номер условия | у = f 2 (t) | номер условия | у = f 2 (t) | ||||
| Рис. 0-2 | Рис. 3-6 | Рис. 7-9 | Рис. 0-2 | Рис. 3-6 | Рис. 7-9 | ||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| 2 – 9cos (π/6 t) | t 2 + 2t | – 3cos (π/3 t) | – 5cos (π/6 t) | 3 t 2 – 4 | 3sin (π/6 t) | ||
| 2 – 6cos (π/3 t) | 8cos (π/4 t) | 12sin (π/6 t) | 6cos (π/6 t) | (t + 1)3 | 16 sin2 (π/6 t) | ||
| 2 – 6cos2 (π/6 t) | 2 + 2 t 2 | 10sin2 (π/6 t) | – 9cos2 (π/6 t) | 324cos(π/4 t) | 9cos (π/3 t) | ||
| 6cos (π/6 t) | 2(t + 1)2 | 6 – 4sin (π/6 t) | 6cos (π/3 t) – 4 | 2 t 3 | 2 – 9sin (π/6 t) | ||
| 9cos (π/3 t) + 3 | 2sin(π/4 t) | 12cos (π/3 t) | 2 – 2 cos (π/6 t) | 6 sin (π/4 t) | 9cos (π/3 t) + 6 |
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.
В данной задаче все искомые величины нужно определить только для момента времени t 1=1с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
cos 2α = 1 – 2 sin2 α = 2 cos2 α – 1; sin 2α = 2 sin α · cos α.
Пример К1. Даны уравнения движения точки в плоскости ху:
.
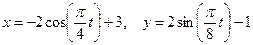Определить уравнение траектории точки; для момента времени t 1 = 1с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
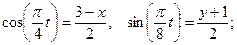
следовательно,
Отсюда окончательно находим следующее уравнение траектории точки (парабола, рис. К1):
|
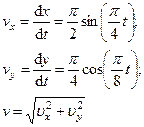
и при t = 1c
v 1x = 1,11 см/с, v 1y = 0,73 cм/c, v 1 = 1,33 см/с.
3. Аналогично найдем ускорение точки:
и при t = 1c
a 1x = 0,87 см/с2, a 1y = –0,12 cм/c2, a 1 = 0,88 см/с.
4. Касательное ускорение найдем, дифференцируя по времени равенство
.
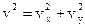Получим:
Числовые значения всех величин, входящих в правую часть выражения, определены выше. Подставив эти числа, найдем сразу, что при t 1 = 1c a 1τ = 0,66 см/с2.
5. Нормальное ускорение точки 
. Подставляя сюда найденные числовые значения a 1 и a 1τ, получим, что при t 1 = 1 c a 1n = 0,58 см/с2.
6. Радиус кривизны траектории ρ = v 2/ a n. Подставляя сюда числовые значения v 1 и a 1n, найдем, что при t 1 = 1c ρ 1 = 3,05 cм.
Ответ: v 1 = 1,33 cм/с, a 1 = 0,88 cм/с2, a 1τ = 0,66 cм/с2, a 1n = 0,58 см/с2, ρ 1 = 3,05 см.
Задача К2
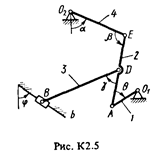
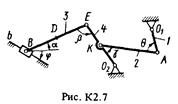
Плоский механизм состоит из стержней 1–4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О 2, шарнирами (рис. К2.0–К2.9). Длины стержней: l 1 = 0,4 м, l 2 = 1,2 м, l 3 = 1,6 м, l 4 = 0,6 м. Положение механизма определяется углами α, β, γ, φ, θ, которые вместе с другими величинами заданы в табл. К2.
| 
| 
| |||
| 
| 
| |||
| 
| 
| 
| ||
Точка D на всех рисунках и точка на рис. К2.7-К2.9 в середине соответствующего стержня. Определить величины, указанные в таблице в столбце «Найти».
Найти также ускорение аА точки А стержня 1, если стержень 1 имеет в данный момент времени угловое ускорение ε1 = 5 с–2.
Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т.е. по ходу или против хода часовой стрелки (например, угол γ на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 – от стержня АЕ по ходу часовой стрелки).
Построение чертежа начинать со стержня, направление которого определяется углом α; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость vB – от точки В к b.
Таблица К2
| Номер условия | Углы | Дано | Найти | ||||||
| α ° | β ° | γ ° | φ ° | θ ° | ω 1, 1/с | ω 4, 1/с | v B, м/с | ||
| – | – | vB, vE, ω 2 | |||||||
| – | – | vA, vD, ω 3 | |||||||
| – | – | vA, vE, ω 2 | |||||||
| – | – | vB, vE, ω 2 | |||||||
| – | – | vB, vA, ω 2 | |||||||
| – | – | vA, vE, ω 3 | |||||||
| – | – | vB, vE, ω 3 | |||||||
| – | – | vA, vD, ω 3 | |||||||
| – | – | vA, vE, ω 2 | |||||||
| – | – | vB, vE, ω 3 |
Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Пример К2. Механизм (рис. К2, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О 1 и О 2, шарнирами.
|
Дано: α = 120°, β = 60°, γ = 90°, φ = 0°, θ = 30°, AD = DE, l 1 = 0,6 м, l 3 = l,2 м, ω1 =5c–1, ε1 = 8 с–2.
|
|
|
