 |
Л. 4 балки с гибкой стенкой
|
|
|
|
Л.4.1 Разрезные балки с гибкой стенкой симметричного двутаврового сечения, несущие статическую нагрузку и изгибаемые в плоскости стенки, как правило, применяют при нагрузке, эквивалентной равномерно распределенной до 50 кН/м, и проектируют из стали с пределом текучести до 345 Н/мм 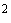 .
.
Л.4.2 Устойчивость балок с гибкой стенкой обеспечивают либо выполнением требований 5.18, а, либо закреплением сжатого пояса, при котором условная гибкость пояса 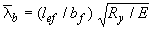 не превышает 0,21 (где
не превышает 0,21 (где  - ширина сжатого пояса).
- ширина сжатого пояса).
Л.4.3 Отношение ширины свеса сжатого пояса к его толщине принимают не более  .
.
Л.4.4 Отношение площадей сечений пояса и стенки  не должно превышать предельных значений
не должно превышать предельных значений  , определяемых по формуле
, определяемых по формуле
 . (Л.12)
. (Л.12)
Л.4.5 Участок стенки балки над опорой укрепляют двусторонним опорным ребром жесткости и рассчитывают его согласно требованиям 9.5.13.
На расстоянии не менее ширины ребра и не более  от опорного ребра устанавливают дополнительное двустороннее ребро жесткости размером согласно Л.4.9.
от опорного ребра устанавливают дополнительное двустороннее ребро жесткости размером согласно Л.4.9.
Л.4.6 Местное напряжение  в стенке балки, определяемое по формуле (37), должно быть не более
в стенке балки, определяемое по формуле (37), должно быть не более  , при этом значение
, при этом значение  вычисляют по формуле (39).
вычисляют по формуле (39).
Л.4.7 При определении прогиба балок момент инерции поперечного сечения брутто балки уменьшают умножением на коэффициент  для балок с ребрами в пролете и на коэффициент
для балок с ребрами в пролете и на коэффициент  - для балок без ребер в пролете.
- для балок без ребер в пролете.
Л.4.8 Прочность разрезных балок симметричного двутаврового сечения, несущих статическую нагрузку, изгибаемых в плоскости стенки, укрепленной только поперечными ребрами жесткости (рисунок Л.1), с условной гибкостью стенки  проверяют по формуле
проверяют по формуле
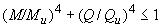 , (Л.13)
, (Л.13)
где  и
и  - значения момента и поперечной силы в рассматриваемом сечении балки;
- значения момента и поперечной силы в рассматриваемом сечении балки;
|
|
|
 - предельное значение момента, вычисляемое по формуле
- предельное значение момента, вычисляемое по формуле
 ; (Л.14)
; (Л.14)
 - предельное значение поперечной силы, вычисляемое по формуле
- предельное значение поперечной силы, вычисляемое по формуле
 . (Л.15)
. (Л.15)
В формулах (Л.14) и (Л.15) обозначено:
 и
и  - толщина и высота стенки соответственно;
- толщина и высота стенки соответственно;
 - площадь сечения пояса балки;
- площадь сечения пояса балки;
 ,
,  - критическое напряжение и отношение размеров отсеков стенки соответственно, определяемые согласно 9.5.3;
- критическое напряжение и отношение размеров отсеков стенки соответственно, определяемые согласно 9.5.3;
 - коэффициент, вычисляемый по формуле
- коэффициент, вычисляемый по формуле
 . (Л.16)
. (Л.16)
Здесь  ;
;
 - минимальный момент сопротивления таврового сечения, состоящего из сжатого пояса балки и примыкающего к нему участка стенки высотой
- минимальный момент сопротивления таврового сечения, состоящего из сжатого пояса балки и примыкающего к нему участка стенки высотой  (относительно собственной оси тавра, параллельной поясу балки);
(относительно собственной оси тавра, параллельной поясу балки);
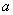 - шаг ребер жесткости.
- шаг ребер жесткости.

Рисунок Л.1 - Схема балки с гибкой стенкой
Л.4.9 Поперечные ребра жесткости, сечение которых принимают не менее указанных в Л.4.8, рассчитывают на устойчивость как стержни, сжатые силой  , определяемой по формуле
, определяемой по формуле
 , (Л.17)
, (Л.17)
где все обозначения принимают по Л.4.8.
Значение  принимают равным не менее значения сосредоточенной нагрузки, расположенной над ребром.
принимают равным не менее значения сосредоточенной нагрузки, расположенной над ребром.
Расчетную длину стержня принимают равной  , но не менее
, но не менее 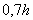 .
.
Симметричное двустороннее ребро рассчитывают на центральное сжатие, одностороннее - на внецентренное сжатие с эксцентриситетом, равным расстоянию от оси стенки до центра тяжести расчетного сечения стержня.
В расчетное сечение стержня включают сечение ребра жесткости и полосы стенки шириной  с каждой стороны ребра.
с каждой стороны ребра.
Л.4.10 Размеры сечений двутавровых балок с гибкой стенкой с ребрами, удовлетворяющие условию (Л.14), определяют по формулам:
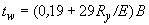 ;
;  ;
;
 ;
;  , (Л.18)
, (Л.18)
где  .
.
Эффективное значение расчетного сопротивления стали  определяют по формуле
определяют по формуле
 . (Л.19)
. (Л.19)
С целью удовлетворения условия (Л.15) при необходимости увеличивают количество ребер жесткости или толщину стенки в отсеках балки, расположенных у опор.
|
|
|
При выборе стали выполняют условие 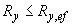 .
.
Л.4.11 В балках по Л.4.1 с условной гибкостью стенки  при действии равномерно распределенной нагрузки или при числе сосредоточенных одинаковых нагрузок в пролете 5 и более, расположенных на равных расстояниях друг от друга и от опор, допускается не укреплять стенку в пролете поперечными ребрами по рисунку Л.1, при этом нагрузка должна быть приложена симметрично относительно плоскости стенки.
при действии равномерно распределенной нагрузки или при числе сосредоточенных одинаковых нагрузок в пролете 5 и более, расположенных на равных расстояниях друг от друга и от опор, допускается не укреплять стенку в пролете поперечными ребрами по рисунку Л.1, при этом нагрузка должна быть приложена симметрично относительно плоскости стенки.
Прочность таких балок проверяют по формуле
 , (Л.20)
, (Л.20)
где  - коэффициент, учитывающий влияние поперечной силы на несущую способность балки и определяемый по формуле
- коэффициент, учитывающий влияние поперечной силы на несущую способность балки и определяемый по формуле
 .
.
При этом принимают  и
и  .
.
Л.4.12 Высоту стенки двутавровых балок минимального сечения с гибкой стенкой без ребер определяют из условия
 , (Л.21)
, (Л.21)
где 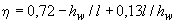 .
.
Эффективное значение расчетного сопротивления стали  определяют по формуле
определяют по формуле
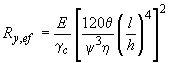 . (Л.22)
. (Л.22)
Для балок минимального сечения из стали с другим расчетным сопротивлением  высоту стенки балки определяют из условия
высоту стенки балки определяют из условия
 . (Л.23)
. (Л.23)
Размеры двутавровых балок минимального сечения с гибкой стенкой без ребер определяют по формулам:
 ;
;  ;
;
 , (Л.24)
, (Л.24)
где 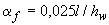 .
.
|
|
|


