Порядок переключения групп передач

 

Для получения последовательно возрастающего геометрического ряда частот вращения шпинделя в пределах n_min-n_max групповые передачи должны переключаться в определённом порядке.

Группу передач, переключаемую в первую очередь, называют основной, во вторую – первой множительной (умножающей, переборной), в третью – второй множительной и т.д., если групп больше, чем три.

В качестве основной, как и любой множительной можно запроектировать любую группу передач, независимо от её расположения в приводе и не меняя этого расположения.

Если обозначить через р_o основную группу, р_I – I множительную, р_II – II множительную, то в рассматриваемом случае возможны следующие варианты:

 

	гр."а", p a =3	гр."б", p б =2	гр."в", p в =2
а)	po	pI	pII
б)	po	pII	pI
в)	pI	po	pII
г)	pI	pII	po
д)	pII	po	pI
е)	pII	pI	po

 

Очевидно, что число вариантов переключений равно числу перестановок групп.

 

Взаимосвязь передаточных отношений в группах передач привода

 

Примем для привода по рис. 2.10 порядок переключения групп и составим для этого случая план соединения шестерен. В рассматриваемой схеме будем считать, что , и это в нижеследующие записи не введём для их упрощения.

 

 

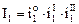
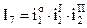
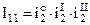
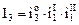
здесь I₁, I₂, I₃,... – полные передаточные отношения привода;

– передаточные отношения в основной группе;

– передаточные отношения в I множительной группе и т.д.

 

Поскольку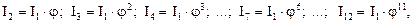

где φ – знаменатель геометрического ряда частот вращения шпинделя, то

 

- в основной группе будет обеспечиваться:

,

т.е. передаточные отношения в основной группе составляют геометрический ряд со знаменателем, равным знаменателю ряда частот вращения выходного вала привода φ;

- в I множительной группе: ,

здесь имеется геометрический ряд со знаменателем

- во II множительной группе: ,

здесь имеется геометрический ряд со знаменателем

 

В общем случае при числе передач в группе р:

 

 

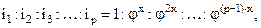
т.е. передаточные отношения в каждой группе передач образуют геометрический ряд со знаменателем , где x, назовём его характеристикой группы передач, равен:

- для основной группы x_о = 1;

- для I множительной x_I = p_о;

- для II множительной x_II = p_о·p_I = x_I· p_I.

 

В общем случае для j-той множительной группы –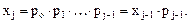

Для последней (k-той) множительной группы – Умножив правую часть последнего выражения на единицу в виде p_k/p_k, получим:

или ,

т.е. характеристику последней множительной группы можно определить, зная число передач в ней и число вариантов скоростей, обеспечиваемых на шпинделе.

 

Развёрнутые структурные формулы

 

Выбранные структуру и порядок переключения групп передач для получения последовательно возрастающего геометрического ряда можно записать с помощью развернутой структурной формулы. Её общий вид следующий:

.

Для рассматриваемого случая и выбранного порядка переключения групп имеем:

или

Из этой формулы можно заключить, что

- привод имеет 12 вариантов;

- привод имеет 3 группы передач: р_a = 3; р_б = 2; р_в = 2;

- групповые передачи расположены на 4 валах;

- порядок переключения групп передач следующий:

р_а – основная; в ней х_а=1 и знаменатель ряда передаточных отношений равен ;

р_б – I множительная; в ней х_б=3 и знаменатель ;

р_в – II множительная; в ней х_в=6 и знаменатель .

 

Все развернутые структурные формулы для случая z=12=3·2·2 (см. п/п. 3.9.1.2) следующие:

а) 12=3(1) ·2(3) ·2(6);	в) 12=3(2) ·2(1) ·2(6);	д) 12=3(4) ·2(1) ·2(2);
б) 12=3(1) ·2(6) ·2(3);	г) 12=3(2) ·2(6) ·2(1);	е) 12=3(4) ·2(2) ·2(1).

 

Предельные величины передаточных отношений в группах передач

 

Практикой станкостроения установлены следующие предельные значения передаточных отношений для любой группы передач:

прямозубых: или

косозубых:

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: