 |
Нахождение наилучшей линейной приближающей функции.
|
|
|
|
Лабораторная работа: метод наименьших квадратов
Одной из самых распространенных задач вычислительной математики является задача статистической обработки данных, и, в частности, составление эмпирических формул для нахождения зависимости одной величины от другой, когда известна таблица их значений, полученных в результате некоторой серии экспериментов.
Общей ЗАДАЧЕЙ здесь является нахождение функции определенного вида, которая наилучшим образом отражает зависимость между величинами. Особенностью данной задачи является то, что не требуется обязательное совпадение данных, полученных в результате измерений со значениями искомой функции в выделенных точках.
Такая постановка задачи является естественной, поскольку:
· результаты измерений могут быть неточными,
· выделенные точки (узлы), как правило, ничем не отличаются от всех остальных и непонятно, почему именно в них нужно требовать точного совпадения данных.
Для того, чтобы сравнивать, какая же из функций лучше отражает данную зависимость, надо договориться, как измерять степень приближения искомой функцией данной зависимости. В качестве меры приближения обычно выбирают одну из следующих:
1. Максимальное по модулю отклонение искомой функции в узлах от данных значений.
2. Сумма модулей отклонений искомой функции в узлах от данных значений.
3. Сумма квадратов отклонений искомой функции в узлах от данных значений.
Первый из перечисленных случаев соответствует приближению искомой функцией в равномерной метрике, второй - в интегральной метрике, а последний - приближению в метрике пространства функций с интегрируемым квадратом. Самым употребляемым на практике является последний случай, а, кроме того, он проще остальных в смысле организации вычислений, в том числе и автоматизированной обработки данных.
|
|
|
ПОСТАНОВКА ЗАДАЧИ.
Дана таблица зависимости функции Y от аргумента X:
| Х | Х1 | Х2 | ……… | Хn |
| У | У1 | У2 | ……… | Уn |
Надо среди функций определить такую (найти значения соответствующих параметров), что сумма квадратов разностей значений этой функции в узлах и величин Yi минимальна.
Обычно ограничиваются функциями одного из следующих видов:
1. Y=ax+b
2. Y=ax2+bx+c (реже полином более высокой степени)
3. Y=axn
4. Y=a ex
5. Y=1/(ax+b)
6. Y=a ln(x)+b
7. Y=a/x+b
8. Y=x/(ax+b)
Нахождение наилучшей линейной приближающей функции.
Разберем подробно решение задачи, когда решение ищется в виде линейной функции (вид 1). Цель - определить коэффициенты a и b таким образом, чтобы величина
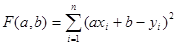
приняла наименьшее значение.
Функция F(a,b) представляет из себя многочлен второй степени относительно величин a и b с неотрицательными значениями, поэтому решение всегда существует. Более того, оно единственно, если узлов больше одного и все они разные.
Известно, что для поиска экстремумов гладких функций нескольких переменных нужно находить критические точки, т.е. те точки, в которых все частные производные функции равны нулю. В нашем случае необходимо решить следующую систему:

Это система двух линейных уравнений с двумя неизвестными a и b.
Перепишем ее в следующем виде:

Введем стандартные в статистике обозначения для моментов:

Тогда наша система перепишется в следующем виде:

которая решается стандартным образом.
Далее, осталось отметить, что раз критическая точка одна, а мы предварительно определили, что у нашей задачи решение есть, то задача решена полностью.
ПРИМЕР нахождения наилучшей линейной функции.
Пусть зависимость задана таблицей
| X | -3 | -1 | |||
| Y |
Для ручного вычисления моментов Mx, My, Mxx, Mxy построим таблицу:
|
|
|
| X | Y | X2 | XY | |
| -3 | -9 | |||
| -1 | -4 | |||
| Сумма | ||||
| Среднее значение (М) | 6.2 | 13.4 |
Отсюда получаем систему
9a+b=13.4 a=0.9
a+b=6.2 или b=5.3
Итак, наилучшая линейная функция имеет вид y=0.9x+5.3
|
|
|


