 |
Нормальное распределение данных
|
|
|
|
Нормальное распределение представляет собой теоретическую гладкую гистограмму в форме колокола без случайных отклонений. Такая кривая представляет идеальный набор данных, в котором большинство чисел сконцентрировано в средней части диапазона значений, а оставшиеся значения с затуханием симметрично расположены по обе стороны от вершины колокола. Такая степень гладкости не присуща реальным данным. На рис. 1 приведена кривая нормального распределения.

Рис. 1
Фактически существует много различных кривых нормального распределения, форма которых напоминает симметричный колокол. Они отличаются расположением центра и масштабом (шириной колокола). Чтобы построить конкретную кривую нормального распределения следует взять базовую кривую в форме колокола, переместить ее по горизонтали в точку, где предполагается разместить центр, а затем растянуть (или сжать). На рис: 2 приведено несколько кривых нормального распределения.
Почему нормальное распределение играет такую важную роль в статистике? Обычно в статистике предполагают, что распределение данных приблизительно соответствует нормальному. Специалисты статистики знают свойства нормального распределения и используют их всякий раз, когда гистограмма похожа на кривую нормального распределения.
Если непрерывная случайная величина имеет плотность распределения
f (x) =  ,
,
то она подчиняется закону нормального распределения. Для построения кривой нормального распределения надо знать два параметра: среднее значение  и стандартное квадратическое отклонение
и стандартное квадратическое отклонение  .
.
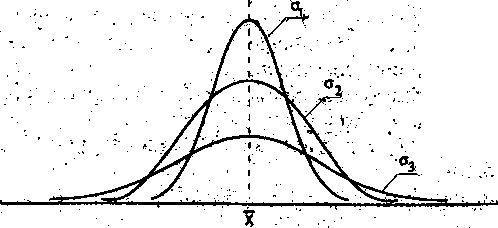
Рис. 2
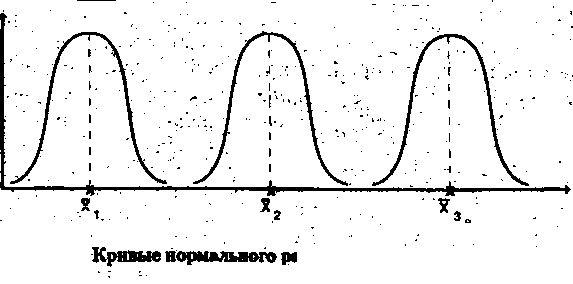
Рис. 3
Если средняя арифметическая не меняется, но растет величина среднего квадратического отклонения, распределение имеет более плосковершинный характер (рис. 2)
|
|
|
На рис. 3 приведено «семейство» кривых нормального распределения с одной и той же величиной среднего квадратического отклонения, но разными средними ( <
<  <
<  ). В этом случае кривая, не меняя своей формы, сдвигается вправо вдоль оси абсцисс.
). В этом случае кривая, не меняя своей формы, сдвигается вправо вдоль оси абсцисс.
Укажем особенности кривой нормального распределения:
1. Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению x = Mo = Me =  , ее величина равна
, ее величина равна 
2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от  , тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной x от
, тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной x от  равновероятны.
равновероятны.
3. Кривая имеет две точки перегиба, находящиеся на расстоянии 
 от
от  .
.
4. При  = const с увеличением
= const с увеличением  кривая становится более пологой. При
кривая становится более пологой. При  = const с изменением
= const с изменением  кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.
кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.
1. В промежутке  ±
±  находится 68,3% всех значений признака. В промежутке
находится 68,3% всех значений признака. В промежутке 
 2
2  находится 95,4% всех значений признака. В промежутке
находится 95,4% всех значений признака. В промежутке 
 3
3  находится 99,7% всех значений признака.
находится 99,7% всех значений признака.
Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другими.
В каком случае можно сказать, что набор данных подчиняется нормальному распределению? Хороший способ заключается в том, чтобы внимательно изучить гистограмму. На рис. 3.3.3 представлены гистограммы для различных выборок объемом 100 значений каждая из нормально распределенного набора данных. Этот рисунок демонстрирует, насколько случайной может быть форма распределения при ограниченном размере выборки.
|
|
|
Уменьшение количества данных приводит к увеличению случайности, поскольку не достаточно информации для представления полной картины распределения.
Действительно ли в реальной жизни все наборы данных подчиняются нормальному распределению? Конечно, нет. Используя гистограмму, важно определить, являются ли данные нормально распределенными. Это особенно важно, если дальнейший анализ предполагает использование стандартных статистических процедур, которые требуют нормального распределения данных. В следующем разделе мы рассмотрим один вид отличия экономических данных от нормального распределения и предложим способ справиться с этой проблемой.
Несимметричное (скошенное) распределение не является ни симметричным, ни нормальным, поскольку значения данных на одной стороне кривой затухают быстрее, чем на другой.
В бизнесе часто можно встретить асимметрию в наборах данных, которые отражают величины, выраженные положительными числами (например, объёмы продаж или размеры активов). Это связано с тем, что такие данные не могут принимать отрицательные значения (наличие границы с одной стороны) и значения не ограничены сверху. В результате на гистограмме много значений данных сконцентрировано около нуля, и количество значений становится все меньше и меньше при движении по горизонтальной оси гистограммы вправо.
Проблема с асимметрией
Одна из проблем, связанных с асимметрией данных, состоит в том, что многие из наиболее распространенных статистических методов (о которых вы узнаете в следующих главах) требуют, чтобы данные были, по крайней мере, приблизительно нормально распределенными. Если эти методы применяют к несимметричным данным, то полученный результат может быть неточным или просто неверным. И даже если результаты получаются в основном корректными, будет определенная потеря эффективности анализа, поскольку не обеспечивается наилучшее использование всей информации, содержащейся в наборе данных.
|
|
|


