Испытание материалов на растяжение и ударную вязкость

Испытания на растяжение относят к самым распространенным видам механических испытаний, при которых определяется прочность и пластичность материала. Результаты экспериментальных исследований механических свойств материала при одноосном растяжении обычно изображают в виде графиков зависимости напряжения от деформации (рис. 2.3). Чаще всего испытания проводят при «комнатной» температуре, т. е. при t = 20 °С (или Т = 293 К), и при постоянной и достаточно малой скорости деформации. При этом силу Р, растягивающую образец, относят к первоначальной площади поперечного сечения F₀, а удлинение образца Dl – к первоначальной расчетной длине образца l₀:

т. е. не учитывают изменение площади поперечного сечения образца и предполагают равномерное деформирование образца по его длине.

 

Рис. 2.3. Диаграмма растяжения

 

Условный предел прочности s_В определяется как отношение максимальной силы P_max к первоначальной площади поперечного сечения образца:

Для определения действительного предела прочности S_b максимальную силу P_max необходимо относить к действительной площади поперечного сечения образца. Поскольку длина образца после деформации , а площадь поперечного сечения равна F, то согласно постоянству объема до и после деформации: , откуда

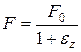
и .

На диаграмме растяжения наблюдаются области упругой деформации, исчезающей после снятия вызвавшей ее нагрузки, и пластической. Между напряжениями и деформациями в области упругости соблюдается закон Гука:

,

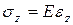где E – модуль упругости при растяжении (модуль Юнга).

Модуль упругости Е является константой материала, характеризующей его жесткость. Величина Е выражает сопротивляемость материала упругой деформации при растяжении. Следует отметить, что величина модуля упругости даже для одного и того же материала не является постоянной и колеблется в некоторых пределах. Однако в инженерных расчетах этой разницей можно пренебречь и принять для большинства материалов одно и то же значение Е как при растяжении, так и при сжатии. Модуль упругости является коэффициентом пропорциональности между нормальным напряжением σ и относительной деформацией ε и выражается зависимостью

Е = σ/ε = tg α,

где α – угол наклона прямолинейной части диаграммы растяжения σ = f (ε) к оси абсцисс.

Аналогично при сдвиге величина G является коэффициентом пропорциональности между касательным напряжением τ и относительным сдвигом γ и называется модулем упругости при сдвиге или модулем сдвига. Величина G выражается зависимостью

G = τ/γ.

В связи с тем что при растяжении или сжатии материал испытывает как продольные ε, так и поперечные ε₁ деформации, их отношение может быть выражено через коэффициент поперечной деформации, называемый также коэффициентом Пуассона μ:

μ = ε₁/ ε.

Коэффициент Пуассона так же, как и модули упругости, является характеристикой упругих свойств материала. Все три константы упругости материала связаны между собой следующей зависимостью:

G = Е/2(1 + μ).

Наибольшее напряжение, при снятии которого остаточные деформации не превышают некоторой заданной малой величины (обычно менее 0,2 %), называют пределом упругости s_УПР.

Если за участком пропорциональности напряжения и деформации следует площадка текучести, соответствующая увеличению деформации при постоянном напряжении (рис. 3.9), то это напряжение называют пределом текучести s_Т. При отсутствии таковой площадки пределом текучести считают напряжение, соответствующее некоторому установленному небольшому уровню деформации (например, 0,2 %), – s_{0,2 .}

Область справедливости закона Гука устанавливается пределом пропорциональности s_ПЦ. Поскольку пропорциональность напряжения деформации обычно выполняется во всей области упругости, при практических расчетах предел пропорциональности принимают равным пределу упругости (или меньше).

Для использования диаграмм растяжения при других, более сложных схемах деформирования напряжение заменяют интенсивностью напряжений s_i, а деформацию 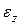– интенсивностью деформаций .

Пластичность характеризуется относительным удлинением и относительным сужением. Относительное удлинение δ – это относительное приращение (l_K – l₀) расчетной длины образца после разрыва к его первоначальной расчетной длине l₀, выраженное в процентах:

Относительное сужение ψ – это отношение разности начальной и конечной площади (S₀ – S_K) поперечного сечения образца после разрыва к начальной площади S₀ поперечного сечения, выраженное в процентах:

Испытания на растяжение не всегда оценивают склонность материала к хрупкому разрушению, поэтому применяют испытания для определения ударной вязкости, отличающиеся от обычных испытаний на растяжение тем, что образец испытывается на изгиб при ударном (динамическом) нагружении.

Ударная вязкость – способность материала сопротивляться динамическим нагрузкам, определяется как отношение затраченной на излом работы А к площади его поперечного сечения F₀ в месте надреза до испытания: КС = А/F₀.

Для испытания (ГОСТ 9454–78) изготавливают стандартные образцы, имеющие форму квадратных брусков с надрезом. Форма надреза может быть
U-образной, V-образной и в виде трещины. Испытывают образцы на маятниковых копрах. Свободнопадающий маятник копра ударяет по образцу со стороны, противоположной надрезу. При этом фиксируется работа, затраченная на излом образца (рис. 2.4).

 

 

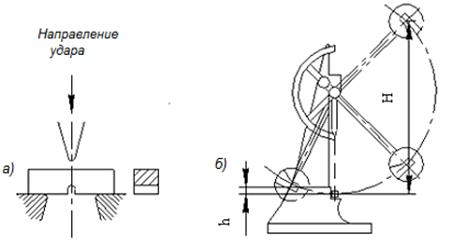
Рис. 2.4. Схема испытания на ударную вязкость:

а – образец; б – маятниковый копер

 

Определение ударной вязкости особенно важно для металлических материалов, работающих при отрицательных температурах и проявляющих склонность к хладноломкости. Чем ниже температура, при которой вязкое разрушение материала переходит в хрупкое, и больше запас его вязкости, тем он надежнее.

 

Определение твердости

Твердость – способность материала сопротивляться проникновению в него другого, более твердого материала. Высокой твердостью должны обладать металлорежущие инструменты (резцы, сверла, фрезы и т. д.), а также поверхностно упрочненные детали. Твердость металла определяют способами Бринелля, Роквелла, Виккерса и др. (рис. 2.5).

Способ Бринелля (ГОСТ 9012–59) основан на том, что в плоскую поверхность металла вдавливают под постоянной нагрузкой закаленный шарик (индентор) (рис. 2.5, а). Диаметр шарика и величину нагрузки устанавливают в зависимости от твердости и толщины испытуемого металла. Испытание выполняют на приборе ТШ (твердомер шариковый): столик прибора с установленным на нем образцом поднимают до соприкосновения с шариком. Груз опускается и вдавливает шарик в испытуемый образец. На поверхности образца образуется отпечаток. Чем больше диаметр отпечатка, тем металл мягче.

 

 

Рис. 2.5. Схемы определения твердости:
а – по Бринеллю; б – по Роквеллу; в – по Виккерсу

 

За меру твердости НВ принимают отношение нагрузки F к площади поверхности отпечатка шарика диаметром D:

НВ = , МПа.

Диаметр отпечатка измеряют оптической лупой, значение твердости определяют по таблице. Метод прост, достаточно точен и пригоден для измерения твердости материалов до НВ 6500 (средний уровень твердости).

Для испытания твердых материалов применяют способ Роквелла (ГОСТ 9013–59), который назван по имени американского металлурга ХХ века С. П. Роквелла, разработавшего этот метод.

По способу Роквелла (рис. 2.5, б) твердость металлов определяют вдавливанием в испытываемую поверхность алмазного индентора в виде конуса с углом при вершине 120° (шкалы А и С) или стального закаленного шарика диаметром ¹/₁₆ дюйма, т. е. 1,588 мм (шкала В). Значение твердости отсчитывают по циферблату индикатора, установленного на приборе.

Твердость по Роквеллу измеряют в условных единицах. За единицу твердости принята величина, соответствующая осевому перемещению наконечника на 0,002 мкм:

, .

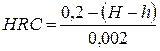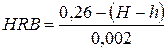При определении твердости способом Виккерса (ГОСТ 2999–75) – от названия английского военно-промышленного концерна «ВИККЕРС» – в поверхность образца вдавливается алмазный индентор (наконечник), имеющий форму правильной четырехгранной пирамиды с двугранным углом при вершине 136° (рис. 2.5, в). При испытаниях применяют нагрузки от 50 до 1000 Н в зависимости от твердости образца.

Числовое значение твердости определяют следующим образом: замеряют с помощью микроскопа длину обеих диагоналей отпечатка после снятия нагрузки и по среднему значению длины диагонали находят в таблице соответствующее значение твердости.

Для измерения твердости металлов в малых объемах (например, в зернах металла) применяют способ определения микротвердости, подобный способу Виккерса.

Для соизмерения значений твердости, определенных различными способами, применяются переводные таблицы (пример: табл. 2.1).

Таблица 2.1

Перевод величин твердости

d10, мм	По Бринеллю НВ, МПа	По Роквеллу	По Виккерсу НV, МПа
НRА	НRС	НRВ
2,34		84,5	65,0	–
2,50		81,0	59,0	–
2,60		79,0	56,0	–
2,68		78,0	53,0	–
2,78		76,0	50,0	–
2,88		74,5	47,5	–
2,98		73,0	44,0	–
3,10		71,0	41,0	–

Для оценки механических свойств материалов и приблизительного значения предела прочности можно использовать значение твердости, определенной по испытаниям способом Бринелля. Эмпирическое соотношение выглядит следующим образом:

σ_В ≈ 0,33НВ_мах,

где σ_В – временное сопротивление; НВ_мах – максимальное значение твердости при нагрузке, с которой начинается плавное понижение твердости.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: