 |
Расчетно-пояснительная записка
|
|
|
|
к курсовому проекту по дисциплине
«Прикладная механика» Проектирование редуктора общего машиностроения
Выполнил: студент группы 4325-280302D
Карманова Виктория Владимировна
Руководитель проекта: доцент кафедры
основ конструирования машин, к.т.н. Хибник Татьяна Алексеевна
Самара 2019
ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Задание №2. Вариант №2.
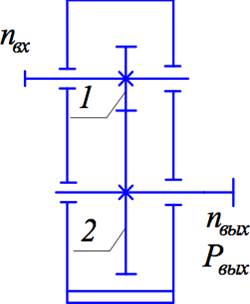 |
Выполнить эскизный проект редуктора общего машиностроения согласно кинематической схеме и исходным данным. Кинематическая схема показана на рисунке 1.
Рисунок 1 - Кинематическая схема редуктора общего машиностроения
Таблица 1- Исходные данные
| Мощность на выходном валу | 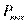 , кВт , кВт
| 3 |
| Частота вращения выходного вала |  , об/мин , об/мин
| 350 |
| Срок службы редуктора |  , ч , ч
| 8000 |
Расчетно–пояснительную записку оформляют согласно стандарту организации [1].
СОДЕРЖАНИЕ
| Введение | 4 |
| 1 Кинематический и энергетический расчет редуктора | 5 |
| 1.1 Определение общего передаточного отношения и выбор электродвигателя | 5 |
| 1.2 Определение частот вращения валов | 5 |
| 1.3 Определение мощностей на валах | 6 |
| 1.4 Определение крутящих моментов на валах | 6 |
| 2 Расчет прямозубой цилиндрической зубчатой передачи | 7 |
| 2.1 Выбор материала зубчатых колес и обоснование термической обработки | 7 |
| 2.2 Определение допускаемых контактных напряжений | 9 |
| 2.3 Определение допускаемых габаритных напряжений | 11 |
| 2.4 Определение габаритных размеров цилиндрической передачи | 12 |
| 2.5 Определение модуля и чисел зубьев | 14 |
| 2.6 Определение геометрических размеров и параметров | 15 |
| 2.7 Проверка прочности по контактным напряжениям | 17 |
| 2.8 Проверка прочности по изгибным напряжениям | 19 |
| 2.9 Расчеты на ЭВМ | 20 |
| 2.10 Определение усилий в зацеплении цилиндрической передачи | 20 |
| 3 Эскизная компоновка | 22 |
| 3.1 Выбор материалов валов | 22 |
| 3.2 Предварительное определение диаметров валов | 22 |
| 3.3 Предварительный подбор подшипников качения | 22 |
| 3.4 Разработка чертежа общего вида | 23 |
|
|
|
ВВЕДЕНИЕ
Основным материалом для изготовления зубчатых колес является сталь, причем не в сыром, а в термически обработанном виде, реже — чугун и пластмассы. Выбор материалов и методов их упрочнения для изготовления зубчатых колес редукторов определяется необходимостью обеспечения прочности, надежности, долговечности, а также технологических требований производства. Кроме того, существуют также и экономические требования, в соответствии с которым материал должен быть по возможности дешевым, а технология изготовления — простой. Эти требования часто противоречат друг другу, поэтому при выборе материалов и их термообработки обычно рассматривают несколько вариантов, чтобы выбрать оптимальный.
Разрушение зубчатых передач чаще всего носит характер усталости выкрашивания от повторных контактных напряжений, а допускаемые контактные напряжения зависят, в основном, от твердости материалов.
Условно все зубчатые передачи в зависимости от твердости рабочих поверхностей подразделяют на две группы: прирабатывающиеся и неприрабатывающиеся.
Колеса прирабатывающихся передач подвергают термообработке: отжигу, нормализации, улучшению, а колеса неприрабатывающихся передач — поверхностной закалке, химико-термической обработке. Режимы термообработки выбирают согласно химическому составу и назначению стали.
1.Кинематический и энергетический расчет редуктора
1.1 Определение общего передаточного отношения и выбор электродвигателя
В качестве электродвигателя используем асинхронные электродвигатели переменного тока серии АИР. Электродвигатели данной серии изготавливаются с различными номинальными частотами вращения валов, а именно 3000, 1500, 1000 и 750 об/мин. В связи с этим выполняем сравнительную оценку передаточных отношений редуктора по формуле(1):
|
|
|
| n н U p = дв n в ых, | (1) |
где
Н
|
Up 1
= 3000 = 8,6
 350 ,
350 ,
Up 2
= 1500 = 4,3
 350 ,
350 ,
Up 3
= 1000 = 2,9
 350 ,
350 ,
Up 4
= 750 = 2,1
 350 .
350 .
Согласно рекомендациям определили вид передачи: зубчатая цилиндрическая (тихоходная ступень), твердость зубьев которой не больше 350 НВ и U=2,5…5,6. Для данного типа зубчатой передачи среди полученных значений наиболее подходящее передаточное отношение Up= 4,3.
Номинальная мощность электродвигателя должна быть не менее потребной, т.е.
P д в ³ P д ¢ в ., поэтому выбираем трехфазный электродвигатель АИР100S4/1410 [2].
P ' дв = P вх = 3,09 кВт.
Данный двигатель имеет следующие характеристики: номинальная мощность 3 кВт, номинальная частота вращения 1500 об/мин, фактическая частота вращения 1410 об/мин.
1.2 Определение частот вращения валов
Частота вращения первого (входного) вала равна асинхронной частоте вращения вала электродвигателя: n 1 = n =1410 об / мин.
Частота вращения второго (выходного) вала известна по заданию:
n 2 = n = 350 об / мин.
 Уточненное значение общего передаточного отношения редуктора:
Уточненное значение общего передаточного отношения редуктора:
 U p =
U p =
n дв n в ых
= n I n II
= 4,1.
1.3 Определение мощностей на валах Мощность на втором (выходном) валу: P II = P = 3 кВт.
Мощность на первом (входном) валу:

|
h P
= 3,09 кВт
.
1.4 Определение крутящих моментов на валах
 Крутящий момент на iтом валу определяется мощностью и частотой вращения по следующей формуле (2):
Крутящий момент на iтом валу определяется мощностью и частотой вращения по следующей формуле (2):
| T = 9,55 ×106 P i, i n i | (2) |
где T i – крутящий момент на i том валу, Н⋅мм;
P i – мощность на iтом валу, кВт;
n i – частота вращения на i том валу, об/мин.
Крутящий момент на первом (входном) валу:
T = 9,55 ×106 P I =20929 Н мм.

|
I
Крутящий момент на втором (выходном) валу:
 T = 9,55 ×106 P II
T = 9,55 ×106 P II
=81857 Н мм.
|
II
2.Расчет зубчатых передач
2.1 Выбор материала зубчатых колес и обоснование термической обработки
|
|
|
В связи с тем, что для редукторов общего машиностроения не предъявляются специфические требования, то материалы изготовления зубчатых колес выбираются в первую очередь исходя из стоимости. К таким маркам относятся стали 40, 45, 40Х, 40 ХН. Данные материалы могут быть подвергнуты термообработке – нормализации или улучшению. В результате термообработки повышается твердость поверхности зубьев, что способствует повышению контактной и изгибной прочности зубьев, а также повышению износостойкости рабочих поверхностей [2].
Передаваемая мощность 3,09.
На основании этого выбрана сталь марки 45 с видом термообработки нормализация и твердость зуба 175НВ в сердцевине.
Тогда твердость поверхности зуба равна: HB 1 = HB 2 +15 =175 +15 =190.
2.2  Определение допускаемых контактных напряжений
Определение допускаемых контактных напряжений
| [ s ] = (s H lim b ) K, H S HL H | (3) |
где 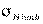 – базовый предел контактной выносливости, МПа;
– базовый предел контактной выносливости, МПа;
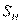 – коэффициент безопасности по контактным напряжениям;
– коэффициент безопасности по контактным напряжениям;  – коэффициент долговечности по контактным напряжениям.
– коэффициент долговечности по контактным напряжениям.
Коэффициенты безопасности по контактным напряжениям для шестерни и колеса можно принять одинаковыми в интервале S H = 1,1...1,3 [2]. Возьмем S H =1,2.
Базовый предел контактной выносливости для шестерни и колеса при нормализации или улучшении определяется по формуле: s Н lim b = 2 HB + 70.
s Н lim1 = 2×190 + 70 = 450,
s Н lim2 = 2×175 + 70 = 420.
Коэффициенты долговечности по контактным напряжениям для шестерни и колеса определяются по формуле (4):
| K = 6 N H, 0 HL N HE | (4) |
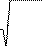
|
0
– где базовое число циклов перемены контактных напряжений;
N HE – расчётное число циклов перемены контактных напряжений.
Базовое число циклов перемены контактных напряжений при твердости поверхности
зубьев
HB < 350
для шестерни и колеса:
|
01
|
02
| N HE = 60 Cnt h K HE, | (5) |
где C – число нагружений зуба за один оборот зубчатого колеса;
n – частота вращения зубчатого колеса, об/мин;
t h – срок службы редуктора, ч;
|
|
|
K HE
– коэффициент эквивалентности по контактным напряжениям.
Число нагружений зуба шестерни и колеса за один оборот в простых однопоточных передачах составляет C = 1.
Частоты вращения зубчатых колес равны частотам вращения валов, на которых они установлены, т.е. шестерня вращается с частотой вращения входного вала, а колесо вращается с частотой вращения выходного вала.
Коэффициент эквивалентности по контактным напряжениям при постоянном режиме
работы принимается
K HE = 1.
Получаем расчетное число циклов:
|
= 60 Cnt h K HE = 60 ×1×1410 × 8000 ×1 = 676800000,
|
Расчетное значение числа циклов перемены контактных напряжений больше базового,
т.е.
N HE > N H 0
, поэтому коэффициент долговечности по контактным напряжениям
принимается
K HL = 1.
Допускаемые контактные напряжения для каждого зубчатого колеса определяются по формуле (3) и их расчеты выглядят следующим образом:
[ s Н ]1
[ s Н ]2
= 450 ×1 = 375,
 1,2
1,2
 = 420 ×1 = 350.
= 420 ×1 = 350.
1,2
В качестве допускаемых контактных напряжений для передачи принимаем наименьшее значение допускаемых контактных напряжений для шестерни и колеса, т.е [ s H ]2 = 350 МПа.
2.3  Определение допускаемых изгибных напряжений
Определение допускаемых изгибных напряжений
| [ s ] = æ s F lim b ö K K F ç S ÷ FL FC è F ø , | (6) |
где s F lim b
– базовый предел выносливости по изгибу, МПа;
S F K FL K FC
– коэффициент безопасности по изгибным напряжениям;
– коэффициент долговечности по изгибным напряжениям;
– коэффициент, учитывающий двустороннее приложение нагрузки на зуб.
Базовый предел выносливости по изгибу для шестерни и колеса при улучшении:
o F lim b = 1,8 × HB.
|
= 1,8 ×190 = 342 МПа,
o F lim2 = 1,8 ×175 = 315 МПа.
Коэффициент безопасности по изгибным напряжениям для шестерни и колеса принимаем одинаковыми: S F = 1,9 [2].
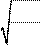
Коэффициенты долговечности по изгибным напряжениям при твердости поверхности
 зубьев
зубьев
HB < 350
для шестерни и колеса определяются по следующей формуле (7):
| K = 6 N F 0 FL N FE, | (7) |
где
N F 0 – базовое число циклов перемены изгибных напряжений;
N FE
– расчётное число циклов перемены изгибных напряжений.
Базовое число циклов перемены изгибных напряжений для шестерни и колеса
|
N = 4 ×106
Расчётное число циклов перемены изгибных напряжений для шестерни и колеса определяется по формуле (8):
| N FE = 60 Cnt h K FE, | (8) |
где C – число нагружений зуба за один оборот зубчатого колеса;
|
|
|
n – частота вращения зубчатого колеса, об/мин;
t h – срок службы редуктора, ч;
K FE
– коэффициент эквивалентности по изгибным напряжениям.
Число нагружений зуба шестерни и колеса за один оборот в простых однопоточных передачах составляет C = 1.
Частоты вращения зубчатых колес равны частотам вращения валов, на которых они установлены, т.е. шестерня вращается с частотой вращения входного вала, а колесо вращается с частотой вращения выходного вала.
Коэффициент эквивалентности по изгибным напряжениям при постоянном режиме
работы принимается
K FE = 1 [2].
Расчетное число циклов равно:
|
FE
|
FE
т.е.
Расчётное значение числа циклов перемены изгибных напряжений больше базового,
N FE > N F 0 , коэффициент долговечности по контактным напряжениям принимается
K FL = 1.
Допускаемые напряжения изгиба для каждого зубчатого колеса определяются по формуле (6):
[ s F ]1
[ s F ]2
= 342 ×1×1 = 180 МПа, 1,9

 = 315 ×1×1 = 165,8 МПа.
= 315 ×1×1 = 165,8 МПа.
1,9
2.4  Определение габаритных размеров цилиндрической передачи
Определение габаритных размеров цилиндрической передачи
| d = 77 3 TK ( U + 1) w 1 y [ s ]2 U bd H , | (9) |
где T – крутящий момент на валу шестерни, Н·мм;
K – коэффициент нагрузки;
U – передаточное отношение цилиндрической передачи;
шестерни;
y bd
– коэффициент ширины зубчатого колеса относительно начального диаметра
[ s H ] – допускаемое контактное напряжение цилиндрической передачи, МПа.
Крутящий момент на валу шестерни равен крутящему моменту на входном валу.
Коэффициент нагрузки предварительно принимается K = 1,5.
 Коэффициент ширины зубчатого колеса относительно начального диаметра шестерни определяется по формуле (10):
Коэффициент ширины зубчатого колеса относительно начального диаметра шестерни определяется по формуле (10):
| y = y ba (U + 1) bd 2 , | (10) |
где расстояния.
y ba
– коэффициент ширины зубчатого колеса относительно межосевого
Полученный коэффициент ширины зубчатого колеса:
y bd
= 0,4 × (4,1 + 1) = 1,02.
 2
2
Значение коэффициента ширины зубчатого колеса относительно начального диаметра
шестерни
y bd £ 1,6.
Диаметр начальной окружности (начальный диаметр) шестерни определяется по формуле (9) и равен:
 20929 ×1,5 × (4,1 + 1)
20929 ×1,5 × (4,1 + 1)
d w 1
(мм)
d wl = 773
1,02 × 3502 × 4,1
= 52,25 мм.
Ширина зубчатых колес определяется по формуле (11):
| b w = y bd d w 1, | (11) |
где y bd
шестерни;
- коэффициент ширины зубчатого колеса относительно начального диаметра
d w 1 - диаметр начальной окружности (начальный диаметр) шестерни, мм.
Расчетная ширина зубчатых передач: b w =1,02 × 52,25» 53 мм.
2.5 Определение модуля и чисел и зубьев
Модуль зацепления определяется из условия изгибной прочности. Модуль зацепления
 m (мм) определяется по формуле (12):
m (мм) определяется по формуле (12):
| m = 2 TKY F d w 1 b w [ s F ]1 , | (12) |
где T – крутящий момент на валу шестерни, Н·мм;
K – коэффициент нагрузки;
Y F – коэффициент формы зуба;
d w 1 – начальный диаметр шестерни, мм;
b w – ширина зубчатых колес, мм;
|
– допускаемое изгибное напряжение шестерни, МПа.
 Расчеты модуля зацепления: m = 2 × 20929 ×1,5 × 4,2 = 0,5285 мм.
Расчеты модуля зацепления: m = 2 × 20929 ×1,5 × 4,2 = 0,5285 мм.
52,3× 53×180
Принимаем минимальное значение модуля при улучшении
m min = 1,5 мм.
Крутящий момент на валу шестерни равен крутящему моменту на входном валу.
Коэффициент формы зуба предварительно принимается Y F
 Число зубьев шестерни определяется по формуле (13):
Число зубьев шестерни определяется по формуле (13):
= 4 [2].
| z = d w 1 1 m, | (13) |
где d w 1 – начальный диаметр шестерни, мм;
m - модуль зацепления, мм.
Число зубьев шестерни равно:
z = 52.3» 34,9
 1 1,5 .
1 1,5 .
Принимаем
z 1 =34.
Число зубьев колеса определяется по формуле (14):
| z 2 = z 1 U, | (14) |
где
z 1 - число зубьев шестерни;
U - значение передаточного отношения.
Получаем число зубьев колеса:
z 2 = 34× 4,1»139,4.
Принимаем
z 2 =139.
После чего определяем фактическое передаточное отношение передачи по формуле
 (15):
(15):
| U ¢ = z 2 z 1, | (15) |
где
z 1 - число зубьев шестерни;
z 2 - число зубьев колеса.
Фактическое отношение передачи по количеству зубьев колеса и шестерни равно:
 U '= 139 = 4,1.
U '= 139 = 4,1.
34
 Отклонение фактического передаточного отношения от исходного значения вычисляется по формуле (16):
Отклонение фактического передаточного отношения от исходного значения вычисляется по формуле (16):
| D U = U - U ¢ 100% U , | 16) |
где U - исходное значение передаточного отношения;
U ' - фактическое передаточное отношение.
Получаем следующее отклонение фактического передаточного отношения от
 исходного: D U = | 4,1- 4,1| ×100% = 0%.
исходного: D U = | 4,1- 4,1| ×100% = 0%.
4,1
2.6  Определение геометрических размеров и параметров Делительное межосевое расстояние определяется по формуле (17):
Определение геометрических размеров и параметров Делительное межосевое расстояние определяется по формуле (17):
| a = m (z 1 + z 2) 2 , | (16) |
где m - модуль зацепления, мм; z 1 - число зубьев шестерни; z 2 - число зубьев колеса.
Расчеты межосевого расстояния выглядят следующим образом:

 a = m (z 1 + z 2) = 1,5 × (34 + 139) = 129,75 мм.
a = m (z 1 + z 2) = 1,5 × (34 + 139) = 129,75 мм.
2 2
Межосевое расстояние при коэффициентах смещения x=0: a w = a = 129,75 мм.
Делительный диаметр шестерни: d 1 = mz 1 =1,5×34 = 51 мм. Делительный диаметр колеса: d 2 = mz 2 =1,5×139 = 208,5 мм.
Начальный диаметр шестерни при коэффициенте смещения x=0: d w 1 = d 1 = 51 мм. Начальный диаметр колеса при коэффициенте смещения x=0: d w 2 = d 2 = 208,5 мм. Угол зацепления при коэффициентах смещения x=0: a w = a = 20° .
Диаметр основной окружности шестерни определяется по формуле (17):
| d b 1 = d w 1 cos a w, | (17) |
где d w 1 - начальный диаметр шестерни, мм;
cos a w - косинус угла зацепления a w .
Результаты диаметра основной окружности шестерни по данной формуле:
d b 1 = 51× cos 20 = 48,5 мм.
Диаметр основной окружности колеса определяется по формуле (18):
| d b 2 = d w 2 cos a w, | (18) |
где d w 2
- начальный диаметр колеса, мм;
cos a w - косинус угла зацепления a w .
Результаты расчетов: d b 2 = 208,5 × cos 20 = 198,3 мм.
Диаметр вершин зубьев шестерни определяется по формуле (19):
| d a 1 = m (z 1 + 2), | (19) |
где m - модуль зацепления, мм;
z 1 - число зубьев шестерни.
Получаем:
d a 1 =1,5 × (34 + 2) = 54 мм.
Диаметр вершин зубьев колеса определяется по формуле (20):
| d a 2 = m (z 2 + 2), | (20) |
где m - модуль зацепления, мм;
z 2 - число зубьев колеса.
Полученный диаметр вершин: d a 2 = 1,5 × (139 + 2) = 211,5 мм. Диаметр впадин зубьев шестерни определяется по формуле (21):
| d f 1 = m (z 1 - 2,5), | (21) |
где m - модуль зацепления, мм;
z 1 - число зубьев шестерни.
Результаты расчетов диаметра впадин: d f 1 = 1,5 × (34 - 2,5) = 47,25 мм. Диаметр впадин зубьев колеса определяется по формуле (22):
| d f 2 = m (z 2 - 2,5), | (22) |
где m - модуль зацепления, мм;
z 2 - число зубьев колеса.
Получаем диаметр впадин зубьев колеса: d f 2 = 1,5 × (139 - 2,5) = 204,75 мм.
Делительный шаг:
P = p m = 4,71 мм.

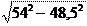 Основной шаг: P b = P cos a w = 4,48 мм.
Основной шаг: P b = P cos a w = 4,48 мм.
Радиус кривизны шестерни: r a 1
= 0,5
= 0,5
=13,2 мм.
Радиус кривизны колеса:
r a 2
= 0,5
= 0,5
= 36,8 мм.
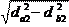
 Коэффициент торцевого перекрытия равен:
Коэффициент торцевого перекрытия равен:


|
P b 4,48
2.7 Проверка прочности по контактным напряжениям
 Коэффициент ширины зубчатого венца относительно диаметра шестерни определяется по формуле:
Коэффициент ширины зубчатого венца относительно диаметра шестерни определяется по формуле:
| y = b w bd d w 1, | (23) |
где b w
– ширина зубчатого колеса, мм;
d w 1 – начальный диаметр шестерни, мм.
Результаты расчетов ширины зубчатого венца: y bd
= 53
 52,3
52,3
= 1,01» 1.
|
Эффективное значение коэффициента неравномерности распределения нагрузки по
ширине зубчатого венца при
HB < 350
и постоянном режиме с периодическими перерывами
в работе: K b = 0,5 × (1,10 +1) = 1,05.
 Окружная скорость шестерни V (м/с) определяется по формуле (24):
Окружная скорость шестерни V (м/с) определяется по формуле (24):
| V = p d w 1 n вх 60000, | (24) |
где n вх
– частота вращения входного вала редуктора, об/мин;
d w 1 – начальный диаметр шестерни, мм.
Расчет окружной скорости шестерни: V = p × 51 × 1410 = 3,76329 м / с.
60000
Коэффициент динамической нагрузки для 8 степени точности при
HB < 350 и
рассчитанной окружной скорости прямозубой передачи
K v = 1,25 [2].
Уточняется коэффициент нагрузки:
K = K V × K b = 1,25 ×1,05 = 1,3125.
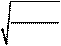 Коэффициент, учитывающий геометрию контактирующих тел, определяется по формуле (25):
Коэффициент, учитывающий геометрию контактирующих тел, определяется по формуле (25):
| Z = 2 H sin 2 a w, | (25) |
где a w
– угол зацепления, град.
Полученное значение коэффициента: Z H =
= 2,41.

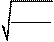 Коэффициент, учитывающий торцевое перекрытие при расчёте по контактным напряжениям для прямозубых цилиндрических передач определяется по формуле (26):
Коэффициент, учитывающий торцевое перекрытие при расчёте по контактным напряжениям для прямозубых цилиндрических передач определяется по формуле (26):
| Z = 4 - ea e 3, | (26) |
где e a
– коэффициент торцевого перекрытия.
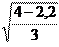 Полученное значение коэффициента: Z e =
Полученное значение коэффициента: Z e =
= 0,78.
Расчётные контактные напряжения s H
(МПа) определяется по формуле (27):
| o = 275 Z Z 2 T вх K (U ¢ р + 1) H H e d 2 b U ¢ w 1 w р , | (27) |
 где Z H
где Z H
– коэффициент, учитывающий геометрию контактирующих тел;
Z e – коэффициент, учитывающий торцевое перекрытие при расчёте по контактным напряжениям;
T вх
– крутящий момент на входном валу, Н·мм;
K – уточненное значение коэффициента нагрузки;
U ¢ р
– уточненное значение передаточного отношения редуктора;
d w 1 – начальный диаметр шестерни, мм;
b w – ширина зубчатого колеса, мм.
Контактные расчетные напряжения равны:
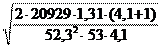 o H = 275 × 2,41× 0,78 ×
o H = 275 × 2,41× 0,78 ×
= 354,587 МП a.
 Проверяем условие прочности по контактным напряжениям: расчетные контактные
Проверяем условие прочности по контактным напряжениям: расчетные контактные
напряжения меньше допускаемых s H
354,587 МПа 350 МПа. Поскольку условие не
выполнено, допустимо увеличение ширины зубчатого колеса b w ; b w =61.
 o H = 275× 2,41× 0,78×
o H = 275× 2,41× 0,78×
= 330,52 МП a.
330,52 МПа 350 МПа. Условие выполнено.
2.8 Проверка прочности по изгибным напряжениям
Коэффициент формы зуба шестерни и колеса находятся линейной интерполяцией:
Y F 1 = 3,76
(при z1=34); Y F 2 = 3,68 (при z2=139).
Расчётные напряжения изгиба s Fi
 определяются по формуле (28):
определяются по формуле (28):
(МПа) для каждого зубчатого колеса и шестерни
| o = 2 T вх KY Fi Fi d b m w 1 w , | (28) |
где i – номер зубчатого колеса;
|
K – уточненное значение коэффициента нагрузки;
Y Fi
– коэффициент формы зуба для рассчитываемого зубчатого колеса;
d w 1 – начальный диаметр шестерни, мм;
b w – ширина зубчатого колеса, мм;
m – модуль, мм.
Получаем следующие значения расчетных напряжений изгиба:
o F 1
o F 2
= 2 × 20929 ×1,31×3,76 = 43,1 МПа,
 52,3× 61×1,5
52,3× 61×1,5
 = 2 ×81857 ×1,31×3,68 = 164,9 МПа.
= 2 ×81857 ×1,31×3,68 = 164,9 МПа.
52,3× 61×1,5
Расчётные напряжения изгиба зубьев для шестерни и колеса меньше допускаемых:
s F 1 [ s F 1 ];43,1 МПа 180 МПа, т.е. условие прочности по изгибным напряжениям для шестерни выполняется.
s F 2 [ s F 2 ];164,9 МПа 165,8 МПа, т.е. условие прочности по изгибным напряжениям для колеса выполняется.
2.9 Расчет на ЭВМ
В результате того, что ручной вариант расчета весьма трудоёмок и ограничен в получении наилучших характеристик передачи, необходимо провести оптимизацию вариантов решения. Определение оптимальных массогабаритных характеристик передачи проводится на ЭВМ. Получен расчет цилиндрической зубчатой передачи на ЭВМ [3]. Полученные результаты представлены в приложении А.
2.10 Определение усилий в зацеплении цилиндрической передачи
В зацеплении цилиндрической прямозубой передачи действует нормальная сила вдоль линии зацепления (нормально к поверхности зубьев в точках контакта). Нормальную силу Fn раскладывают на две составляющие: окружную Ft и радиальную Fr.
 Окружная сила Ft (Н) находится по формуле (29):
Окружная сила Ft (Н) находится по формуле (29):
| F = 2 T вх t d w 1, | (29) |
|
d w 1 – начальный диаметр шестерни, мм.
Значения окружной силы равны:
F = 2 × 20929 = 800,34 H.

t 52,3
Радиальная сила Fr (Н) определяется по формуле (30):
| F r = F t tg a w, | (30) |
где F t
- окружная сила, Н.
Полученные значения радиальной силы:
F r = 800,34× tg 20 = 260,05 Н,
. Нормальная сила Fn (Н) равна:
F n =
F t
 cos a w
cos a w
= F r =
 sin a w
sin a w
= 800,34 = 841,53 H.
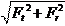
 cos 20
cos 20
3.Эскизная компоновка
3.1 Выбор материала валов
В проектируемых редукторах рекомендуется применять термически обработанные среднеуглеродистые и легированные стали 45, 40Х, одинаковые для быстроходного и тихоходного вала. Механические характеристики сталей для изготовления валов были определены по справочным данным.
НВ[175-190] — 45 — вид термообработки нормализация и улучшение.
3.2 Предварительное определение диаметров вылов
Ориентировочные значения диаметров валов определяются из условия прочности на чистое кручение по заниженному допускаемому напряжению кручения.
 Наружный диаметр вала определяется по формуле (34):
Наружный диаметр вала определяется по формуле (34):
| d = T i i 3 0, 2 éë t ùû кр , | (31) |
где
éë t кр ùû – допускаемое напряжение кручения, МПа.
Допускаемое напряжение кручения для данных валов:
[ t ] кр
=10 Н / мм 2,[ t ]
|
|
= 20 Н / мм 2
.
 Таким образом, полученные диаметры валов (входного и выходного) равны следующим значениям:
Таким образом, полученные диаметры валов (входного и выходного) равны следующим значениям:
 d 1 = =
d 1 = =
 кратное 5: d 1 = 25 мм.
кратное 5: d 1 = 25 мм.
= 21,873 мм. Принимаем значение диаметра входного вала
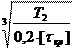 d 2 =
d 2 =
= = 27,353 мм
. Принимаем значение диаметра выходного
вала кратное 5: d 2 = 30 мм.
3.3 Предварительный подбор подшипников качения
Для опор валов цилиндрических прямых и косозубых колёс редукторов применяют чаще всего шариковые радиальные однорядные подшипники. Пр
|
|
|


