 |
Древнеиндийское доказательство
|
|
|
|
Оглавление
1 Введение
а) Цели работы
2 Жизнеописание Пифагора
3 Пифагорейская школа
4 Смерть Пифагора
5 Теорема Пифагора
а) С какого времени известна
б) Способы доказательства
в) Различные задачи на теорему
г) Интересные факты о теореме
6 Практическая часть
а) Собственные задачи
б) Кроссворд
в) Видео
7 Выводы
Введение
1. Цель работы:
Узнать о жизни и деятельности Пифагора, выяснить кто и когда таки открыл теорему Пифагора: действительно ли это был Пифагор. Найти и разобрать разные способы доказательства этой теоремы – от древности и до наших дней. Найти старинные задачи на применение теоремы Пифагора и попытаться решить некоторые из них самим.
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о “пифагоровых штанах” — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Открытие теоремы Пифагором окружено ореолом красивых легенд, которые мы попытались отыскать и изложить в нашем реферате.
|
|
|
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвопринашенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.
2. Жизнеописание Пифагора
Пифагор Самосский – великий греческий учёный. Его имя знакомо каждому школьнику. Если попросят назвать одного древнего математика, то абсолютное большинство назовёт Пифагора. Его известность связана с названием теоремы Пифагора. Хотя сейчас уже мы знаем, что эта теорема была известна в древнем Вавилоне за 1200 лет до Пифагора, а в Египте за 2000 лет до него был известен прямоугольный треугольник со сторонами 3, 4, 5, мы по-прежнему называем её по имени этого древнего учёного. Про жизнь Пифагора достоверно почти ничего не известно, но с его именем связано большое количество легенд.
Пифагор родился в 570 году до н. э на острове Самос. Отцом Пифагора был Мнесарх – резчик по драгоценным камням. Мнесарх, по словам Апулея, «славился среди мастеров своим искусством вырезать геммы», но стяжал скорее славу, чем богатство. Имя матери Пифагора не сохранилось. Пифагор имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".) Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский. Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Он направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встретился с другим ученым - Фалесом. Тот посоветовал ему отправиться за знаниями в Египет, что Пифагор и сделал. В 550 году до н. э Пифагор принимает решение и отправляется в Египет. Итак, перед Пифагором открывается неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям, охраняемым кастой жрецов, лежит через религию.
|
|
|
Вместе с египетскими мальчиками сел за известняковые пластинки и он, возмужалый Эллин с черной курчавой бородой. Очень скоро Пифагор далеко обогнал своих однокашников. Но школа писцов была лишь первой ступенью на пути к тайному знанию. После одиннадцати лет обучения в Египте Пифагор отправляется на родину, где по пути попадает в Вавилонский плен. Там он знакомится со здешней наукой, которая была более развита, чем египетская. Вавилоняне умели решать линейные, квадратные и некоторые виды кубических уравнений. Они успешно применяли теорему Пифагора более чем за 1000 лет до него самого. Сбежав из плена, он не смог долго оставаться на родине из-за царившей там атмосферы насилия и тирании. Он решил переселиться в Кротон. Именно здесь начинается самый славный период в жизни Пифагора.
3. Пифагорейская школа
В Кротоне великий ученый учреждает нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Члены союза должны были придерживаться определённых принципов: во-первых, стремиться к прекрасному и славному, во-вторых, быть полезными, в-третьих, стремиться к высокому наслаждению. Система морально-этических правил, завещанная Пифагором своим ученикам, была собрана в своеобразный моральный кодекс пифагорейцев «Золотые стихи», которые пользовались большой популярностью в эпоху Античности, эпоху Средневековья и эпоху Возрождения. Пифагорейская система занятий состояла из трёх разделов:
|
|
|
1 учения о числах – арифметике,
2 учения о фигурах – геометрии,
3 учения о строении Вселенной – астрономии.
Система образования, заложенная Пифагором, просуществовала много веков. Пифагорейцы учили, что Бог положил числа в основу мирового порядка. Бог – это единство, а мир – множество и состоит из противоположностей. То, что приводит противоположности к единству и соединяет всё в космос, есть гармония. Гармония является божественной и заключается в числовых выражениях. Кто до конца изучит гармонию, сам станет божественным и бессмертным. Музыка, гармония и числа были неразрывно связаны в учении пифагорейцев. Математика и числовая мистика были фантастически перемешаны в нём. Пифагор считал, что число есть сущность всех вещей и что Вселенная представляет собой гармоническую систему чисел и их отношений. Школа Пифагора много сделала, чтобы придать геометрии характер науки.
Основной особенностью метода Пифагора было объединение геометрии с арифметикой. Он много занимался пропорциями и прогрессиями и, вероятно, подобием фигур, так как ему приписывают решение задачи: "По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй". Пифагор и его ученики ввели понятие о многоугольных, дружественных, совершенных числах и изучали их свойства. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что "поставил арифметику выше интересов торговца". Пифагор одним из первых считал, что Земля имеет форму шара и является центром Вселенной, что Солнце, Луна и планеты имеют собственное движение, отличное от суточного движения неподвижных звезд. Учение пифагорейцев о движении Земли Николай Коперник воспринял как предысторию своего гелиоцентрического учения. Недаром церковь объявила систему Коперника "ложным пифагорейским учением".
|
|
|
Пифагорейская школа положила начало математическим наукам. Числа понимались как суть всего существующего, им придавался мистический смысл. Основу пифагорейской математики составляет учение о декаде: 1+2+3+4=10. Эти четыре числа описывают все процессы, происходящие в мире. В частности, декада отображает законы музыкальной гармонии: через нее выражаются основные музыкальные интервалы - октава (2:1), квинта (3:2), кварта (4:3). Пифагорейцам принадлежит учение о музыке сфер и о музыкальном звукоряде, отражающем гармонию Солнечной системы, где каждой планете соответствует определенная нота, а все вместе они создают интервалы музыкальной гаммы. Ими же положено и начало музыкальной психологии: музыка использовалась как средство воспитания и исцеления души и тела. В пифагорейской школе начали развиваться астрономия и медицина. Ею создано множество аллегорических комментариев Гомера, а также грамматика греческого языка.
В школе Пифагора открытия учеников приписывались учителю, поэтому практически невозможно определить, что сделал сам Пифагор, а что его ученики. Споры ведутся вокруг пифагорейского союза уже третье тысячелетие, однако общего мнения так и нет. У пифагорейцев было множество символов и знаков, которые были своего рода заповедями: например, «через весы не шагай», т.е. не нарушай справедливости; огня ножом не вороши», т. е. не задевай гневных людей обидными словами.
Но главным пифагорейским символом - символом здоровья и опознавательным знаком – была пентаграмма или пифагорейская звезда – звёздчатый пятиугольник, образованный диагоналями правильного пятиугольника. Членами пифагорейского союза были жители многих городов Греции. В своё общество пифагорейцы принимали и женщин. Союз процветал более двадцати лет, а потом начались гонения на его членов, многие из учеников были убиты.
Таким образом, пифагорейцев можно считать родоначальниками гуманитарной, естественной, точной и систематической наук.
4. Смерть Пифагора
О смерти самого Пифагора ходило много самых разных легенд. Но учение Пифагора и его учеников продолжало жить.
Относительно того, как умер Пифагор, общего мнения нет. Некоторые говорят, что он был убит собственными учениками; другие говорят, что он бежал из Кротона с небольшой группой последователей и, попав в засаду, сгорел в подожженном доме. По сообщениям Дикеарха следовало, что Пифагор умер в Метапонте: “Пифагор умер, бежав в метапонтийский храм муз, где провел сорок дней без пищи”.
|
|
|
Согласно легендам Пифагор был сыном бога Гермеса. Другая легенда гласит, что однажды река Кас, увидев его, приветствовала философа человеческим голосом. Пифагор соединял в себе черты мудреца, мистика, математика и пророка, тщательного исследователя числовых закономерностей мира и религиозного реформатора. При этом его приверженцы почитали его чудотворцем.
Еще одна версия говорит о том, что в горящем доме ученики образовали мост из тел, живыми войдя в огонь, для того, чтобы их учитель прошел по нему и спасся, и только впоследствии Пифагор умер от разрыва сердца, скорбя по поводу кажущейся тщетности своих усилий по просвещению и служению человечеству. Выжившие его ученика пытались продолжать его учение, но они всякий раз подвергались гонениям, и к сегодняшнему дню мало что осталось от свидетельств величия этого философа.
Легенда о смерти Пифагора
Сонную тишину ночного Метапонта прорезал ужасный крик. Послышалось падение на землю тяжелого тела, топот убегающих ног, и все смолкло. Когда ночной караул прибыл на место происшествия, в колеблющемся свете факелов все увидели распростертого на земле старца, и неподалеку от него - мальчик 12 с лицом, перекошенным от ужаса.
- Кто это? - спросил начальник караула у мальчика
- Это Пифагор, - ответил тот.
- Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов, и выходил только ночью. Они выследили его и убили.
- Сколько их было?
- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него. Начальник караула стал на колени и приложил руки к груди старца.
- Конец, - сказал начальник.
5. Теорема Пифагора
а) В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что именно Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных конкретных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет немецкого писателя-романиста Шамиссо:
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать, А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары. Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I.
Несколько больше было известно о теореме Пифагора вавилонянам. В одном тексте, относимом ко времени Хаммураби, т.е. к 2000 году до нашей эры, приводится приближенное вычисление гипотенузы прямоугольного треугольника; отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.
Геометрия у индусов была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 8 века до нашей эры. Наряду с чисто ритуальными предписаниями, существуют и сочинения геометрически теологического характера, называемые Сульвасутры. В этих сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.
В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена нередко употреблялся как символ математики.
Некоторые переводы знаменитой теоремы:
У Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен
квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннариции:
«Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол»
В Geometry Culmonensis (около 1400года) теорема читается так (в переводе):
“Итак, площадь квадрата, измеренного по длиной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу”
В русском переводе евклидовых «Начал», теорема Пифагора изложена так:
«В прямоугольном треугольнике квадрат из стороны, противолежащей
прямому углу, равен сумме квадратов из сторон, содержащих прямой угол». Как видим, в разных странах и разных языках существуют различные
варианты формулировки знакомой нам теоремы. Созданные в разное время и в 9 разных языках, они отражают суть одной математической закономерности, доказательство которой также имеет несколько вариант
б) В настоящее время известно более трехсот доказательств теоремы Пифагора. В нашей проектной работе мы решили перечислить и разобрать некоторые наиболее интересные доказательства.
 Древнекитайское доказательство.
Древнекитайское доказательство.
Иначе называется «Стул невесты» из-за похожей на стул фигуры, которая получается в результате всех построений. Если мысленно отрезать от первого чертежа два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a.
Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c2=a2+b2.
 Доказательство Евклида
Доказательство Евклида
В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB, BC==BD и FBC=d+ABC=ABD. Но SABD=1/2 SBJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=1\2 SABFH (BF—общее основание, АВ—общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD= SABFH. Аналогично, используя равенство треугольников ВСК. и АСЕ, доказывается, что SJCEL=SACKG.
Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED, что и требовалось доказать. Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли «ходульным» и «надуманным». Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений 1-й книги «Начал». Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь.
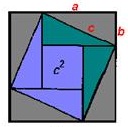
Древнеиндийское доказательство
 Доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».
Доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».
Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с. Катеты треугольника назовем а и b. В соответствии с чертежом сторона внутреннего квадрата это (a-b).
Используйте формулу площади квадрата S=c2, чтобы вычислить площадь внешнего квадрата.
И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b)22+4*1\2*a*b.
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c2=(a-b)2+4*1\2*a*b. В результате решения вы получите формулу теоремы Пифагора c2=a2+b2. Теорема доказана.
|
|
|


