Главная | Обратная связь | Поможем написать вашу работу!

Принципы разработки алгоритмов и программ

Типы алгоритмических процессов
По структуре выполнения алгоритмы и программы делятся на три вида:

· Линейные

· Ветвящиеся

· Циклические

Линейный алгоритм (линейная структура) – это такой алгоритм, в котором все действия выполняются последовательно друг за другом и только один раз. Схема представляет собой последовательность блоков, которые располагаются сверху вниз в порядке их выполнения. Первичные и промежуточные данные не оказывают влияния на направление процесса вычисления.

Алгоритмы разветвляющейся структуры
На практике часто встречаются задачи, в которых в зависимости от первоначальных условий или промежуточных результатов необходимо выполнить вычисления по одним или другим формулам.

Такие задачи можно описать с помощью алгоритмов разветвляющейся структуры. В таких алгоритмах выбор направления продолжения вычисления осуществляется по итогам проверки заданного условия. Ветвящиеся процессы описываются оператором IF (условие).

Циклические вычислительные процессы
Для решения многих задач характерно многократное повторение отдельных участков вычислений. Для решения таких задач применяются алгоритмы циклической структуры (циклические алгоритмы). Цикл – последовательность команд, которая повторяется до тех пор, пока не будет выполнено заданное условие. Циклическое описание многократно повторяемых процессов значительно снижает трудоемкость написания программ.
Существуют две схемы циклических вычислительных процессов.

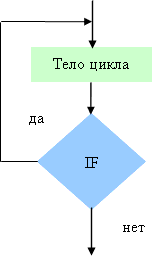
Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла. В том случае, если условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.

Особенностью второй схемы является то, что цикл выполняется хоты бы один раз, так как первая проверка условия выхода из цикла осуществляется после того, как тело цикла выполнено.

Существуют циклы с известным числом повторений и итерационные циклы. При итерационном цикле выход из тела цикла, как правило, происходит при достижении заданной точности вычисления.

30. Язык программирования Pascal был назван в честь французского учёного Блеза Паскаля, который еще в 1642 г. изобрел первую механическую счётную машину. Она представляла собой систему взаимодействующих колёсиков, каждое из которых соответствовало одному разряду десятичного числа и содержало цифры от 0 до 9. Когда колёсико совершало полный оборот, следующее сдвигалось на одну цифру (это похоже на принцип ручных счетов). Машина Паскаля умела только складывать и вычитать.Язык - система знаков. Язык ЭВМ (машинный язык) - двоичная знаковая система. Поэтому, чтобы компьютер мог понять написанную программу, она должна быть переведена на язык, понятный компьютеру. Этот процесс перевода называется трансляцией.Существуе два различных подхода к трансляции – интерпретация и компиляция. Интерпретатор перводит и выполняет программу строка за строкой. Компилятор переводит программу целиком, а затем выполняет её.Символы языка - это элементарные знаки, используемые при составлении текстов. Алфавит языка - набор таких символов. Алфавит языка Turbo Pascal 7.0 включает:все латинские прописные и строчные буквы,арабские цифры (0 – 9),символы + - * / = < >,.;: ’ _ () { } и др.

31. Операторы языка TURBO PASCAL, исполняемые и неисполняемые. Операторы (команды). Оператор — это наиболее крупное и содержательное понятие языка: каждый оператор представляет собой законченную фразу языка и определяет некоторый вполне законченный этап обработки данных. В состав опеpатоpов входят:ключевые слова;данные;выpажения и т.д.Операторы подpазделяются на исполняемые и неисполняемые. Неисполняемые опеpатоpы пpедназначены для описания данных и стpуктуpы пpогpаммы, аисполняемые — для выполнения pазличных действий (напpимеp, опеpатоp пpисваивания, опеpатоpы ввода и вывода, условный оператор, операторы цикла, оператор процедуры и дp.).

32,33. Оператор ввода. Способы ввода данных.

Оператор вывода.Для того чтобы получить данные, вводимые пользователем вручную (т.е. с консоли), применяются команды

read (<список_ввода>)
readln (<список_ввода>)
Первая из этих команд считывает все предложенные ей данные, оставляя курсор в конце последней строки ввода, а вторая - сразу после окончания ввода переводит курсор на начало следующей
строки. В остальном же их действия полностью совпадают.

Список ввода - это последовательность имен переменных, разделенных запятыми.

Например, при помощи команды

readln(k, x, c, s);
{k:byte; x:real; c:char; s:string}
программа может получить с клавиатуры данные сразу для четырех переменных, относящихся к различным типам данных.

Вводимые значения необходимо разделять пробелами, а завершать ввод - нажатием клавиши Enter.

Ввод данных заканчивается в тот момент, когда последняя переменная из списка ввода получила свое значение.

Следовательно, вводя данные при помощи приведенной на слайде выше команды, вы можете нажать Enter четыре раза - после каждой из вводимых переменных, - либо же только один раз, предварительно введя все четырепеременные в одну строчку (обязательно нужно разделить их пробелами).

Если же программе все-таки необходимо получить с консоли значение для boolean -величины, придется действовать более хитро:

Øвводить оговоренный символ, а уже на его основе присваивать логической переменной соответствующее значение.
Пример ввода и вывода на Паскале:

repeat
writeln('Согласны ли Вы с этим утверждением?');
writeln('y - да, n - нет');
readln(c); {c:char}
case c of
'y': b:=true;
'n': b:=false;
else: writeln('Ошибка!');
end;
until (c='n') or (c='y');

Второе исключение: строки, хотя они и не являются базовым типом, вводить тоже разрешается.

Признаком окончания ввода строки является нажатие клавиши Enter, поэтому все следующие за нею переменные необходимо вводить с новой строчки.

Вывод на консоль

Для того чтобы вывести на экран какое-либо сообщение, воспользуйтесь процедурами

write(<список_вывода>)
writeln(<список_вывода>)

Первая из них, напечатав на экране все, о чем ее просили, оставит курсор в конце выведенной строки, а вторая переведет его в начало следующей строчки.

Список вывода может состоять из нескольких переменных или констант, записанных через запятую; все эти переменные должны иметь тип либо базовый, либо строчный.

Например:

writeln(a, b, c);

Переменные, составляющие список вывода, могут относиться к целому, вещественному, символьному или булевскому типам.

В качестве элемента списка вывода кроме имен переменных могут использоваться выражения и строки.

Оператор Writеln без параметров реализует пропуск строки и переход к началу следующей строки.

Если для вывода информации просто перечислять переменные через запятую, товыводимые символы окажутся "слепленными".

Чтобы этого не случилось, нужно позаботиться о пробелах между выводимыми переменными:

writeln(a, ' ', b, ' ', c);

Но предпочтительнее задать для всех (или хотя бы для некоторых) переменных формат вывода:

writeln(a:5, b, c:20:5);

Если число длиннее, чем отведенное под него пространство, количество позиций будет автоматически увеличено.

Если же выводимое число короче заданного формата, то спереди к нему припишутся несколько пробелов.

Таким образом можно производить вывод красивыми ровными столбиками, а также следить за тем, чтобы переменные не сливались. это называется форматированный вывод данных, т.е при таком действии вывод подгоняется под определенный формат.

35. Переменные типы переменных. Константы. Переменная - это элемент программы, предназначенный для коррекции, хранения, передачи данных внутри программы. Перед тем как приступать к созданию очередной программы, необходимо объявить (в разделеvar) все используемые нами в дальнейшем переменные.Чтобы постоянно не прописывать много раз одно и тоже число (которое может окажется слишком громоздким), символ или строку, в Турбо Паскаль предусмотрено использование констант. Константа - это идентификатор, который обозначает некоторую не меняющуюся величину заданного программистом типа. Константы объявляются в соответствующем разделе - разделе const.В Турбо Паскаль представлены следующие виды констант:Целочисленные константы определяются числами, записанными либо в десятичной, либо в шестнадцатеричной системе счисления. Эти числа должны использоваться без десятичной точки.Вещественные константы могут быть определены числами, записанными в десятичной системе счисления с применением десятичной токи.Символьная константа - некоторый символ, заключенный в апострофы.Строковые константы - последовательность любых символов, которая заключена в апострофы.Типизированные константы - это инициализированные переменные (каждой такой константе ставится в соответствие имя, тип и начальное значение). Они могут быть использованы в программе наравне с обычными переменными.

36. Алгоритмы линейной структуры Алгоритмы линейной структуры – это самые простые алгоритмы, которые используются тогда, когда в программе нужно описать обычную последовательность действий, не содержащую ветвлений или циклов.

37. Разветвляющиеся вычислительные процессы Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направление ветвления выбирается логической проверкой, в результате которой возможны два а: «да» — условие выполнено и «нет» — условие не выполнено.
Следует иметь в виду, что, хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определенного условия (или условии), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.

38. Оператор безусловного перехода. Помимо операторов условного перехода существует также оператор безусловного перехода goto. Формат:

goto метка

Оператор goto переходит при выполнении программы к определенному оператору программы, перед которым находится метка. Метка должна быть описана в разделе описания меток той программы (процедуры или функции), в которой она используется. Нельзя перейти из одной процедуры или функции в другую.

Необходимо, чтобы в программе существовал оператор, отмеченный указанной меткой. Она записывается перед оператором и отделяется от него двоеточием.

39. Оператор условного перехода. Оператор условного перехода в Турбо Паскаль имеет вид:

if условие then оператор 1 else оператор 2;

условие - это логическое выражение, в зависимости от которого выбирается одна из двух альтернативных ветвей алгоритма. Если значение условия истинно (TRUE), то будет выполняться оператор 1, записанный после ключевого слова then. В противном случае будет выполнен оператор 2, следующий за словом else, при этом оператор 1 пропускается. После выполнения указанных операторов программа переходит к выполеннию команды, стоящей непосредственно после оператора if.

Необходимо помнить, что перед ключевым словом else точка с запятой никогда не ставится!

else - часть в операторе if может отсутствовать:

if условие then оператор 1;

Тогда в случае невыполнения логического условия управление сразу передается оператору, стоящему в программе после конструкции if.

Следует помнить, что синтаксис языка допускает запись только одного оператора после ключевых слов then и else, поэтому группу инструкций обязательно надо объединять в составной оператор (окаймлять операторными скобками begin... end). В противном случае возникает чаще всего логическая ошибка программы, когда компилятор языка ошибок не выдает, но программа тем не менее работает неправильно.

40. Циклические вычислительные процессы. ля решения многих задач характерно многократное повторение отдельных участков вычислений. Для решения таких задач применяются алгоритмы циклической структуры (циклические алгоритмы). Цикл – последовательность команд, которая повторяется до тех пор, пока не будет выполнено заданное условие. Циклическое описание многократно повторяемых процессов значительно снижает трудоемкость написания программ. Существуют две схемы циклических вычислительных процессов. Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла. В том случае, если условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.

44. Итерационные вычислительные процессы.

Оператор цикла с проверкой условия после тела цикла.

Итерационные циклы отличаются от циклов с параметром тем, что в них заранее неизвестно число повторений.

Пусть мы отправляемся за грибами и возвращаемся домой, когда корзина наполнится. Все грибники делятся на 2 категории:

Смотрят, есть ли место в корзине, а уже потом срывают грибы, если их можно поместить в корзину. (Правда, в жизни таких грибников встречать не приходилось)

Сначала срывают грибы, а уже потом думают, как их положить в корзину.

Отсюда получаются два варианта реализации итерационных циклов: с предусловием и с постусловием.

В цикле с предусловием сначала проверяется условие, а потом делается шаг. Грибник придет с полной или почти полной корзиной. В цикле с постусловием – сначала шаг, а потом проверка. Как всякий нормальный грибник, этот принесет полную или слегка переполненную корзину.

Какой алгоритм выбрать? Это зависит от конкретной задачи.

Если, сделав шаг без проверки, можно свалиться в яму, то лучше проверка вначале (как слепой с палочкой). Ну, а если шаг без проверки вас не пугает, то можно отложить ее до завершения шага.

Нужно также проанализировать событие, которого мы ожидаем. Если оно может случиться до первого шага, то нужен цикл с предусловием. А если событие не может случиться до первого шага, то нужен цикл с постусловием.

45. Подпрограммы: процедуры и функции.При решении новых задач можно попытаться воспользоваться ранее написанными программами. Алгоритм, ранее разработанный и целиком используемый в составе других алгоритмов, называется вспомогательным. Применение вспомогательных алгоритмов позволяет разбить задачу на части, структурировать ее.

Вся программа условно может быть разделена на две части: основную и вспомогательную. В основной части производится простейшая обработка информации, организуется обращение к разным вспомогательным модулям (подпрограммам).

Вспомогательный алгоритм тоже может вызывать другие вспомогательные, длина такой цепочки вызовов теоретически не ограничена. Здесь и далее следующие пары слов используются как синонимы: алгоритм и программа, вспомогательный алгоритм и подпрограмма, команда и оператор, программа и модуль. Вспомогательными и основными алгоритмы являются не сами по себе, а по отношению друг к другу.

При использовании вспомогательных алгоритмов необходимо учитывать способ передачи значений исходных данных для них и получения результата от них. Аргументы вспомогательного алгоритма — это переменные, в которых должны быть помещены исходные данные для решения соответствующей подзадачи. Результаты вспомогательного алгоритма — это также переменные, где содержаться результаты решения этих подзадач, а также результатом может быть конкретное действие, которое совершает компьютер под действием подпрограммы.

Подпрограммы могут быть двух видов: подпрограмма без параметров и подпрограмма с параметрами. Обращение к подпрограмме может быть организовано из любого места основной программы или другой подпрограммы сколько угодно раз.

При работе с подпрограммами важными являются понятия формальных и фактических параметров. Формальные параметры — это идентификаторы входных данных для подпрограммы. Если формальные параметры получают конкретные значения, то они называются фактическими. Формальные параметры могут получить конкретные значения только в той программе, где производится обращение к данному модулю-подпрограмме. Тип и порядок записи фактических параметров должны быть такими же, как и формальных параметров. В противном случае результат работы программы будет непредсказуемым. Из этого следует, что фактические параметры используются при обращении к подпрограмме из основной, а формальные параметры — только в самом модуле.

Подпрограмма с параметрами используется для записи многократно повторяющихся действий при разных исходных данных. Подпрограммы с параметрами можно разделить на два типа: подпрограммы-функции и просто подпрограммы с параметрами (их называют процедурами).

При составлении подпрограмм с параметрами надо соблюдать следующие правила:

1) каждая подпрограмма имеет свое имя и список формальных параметров;

2) процедура из основной программы вызывается командой вызова, которая по форме ничем не отличается от вызова команды исполнителя. Результат присваивается одной или нескольким переменным, которые находятся в списке формальных параметров. Но результатом могут быть, конечно, не только значения переменных, но какое либо действие, выполненное ЭВМ.

46. Локальные и глобальные переменные. Любые идентификаторы, введенные внутри какого-либо блока (процедуры, функции) для описания переменных, констант, типов, процедур, называются локальными для данного блока. Такой блок вместе с вложенными в него модулями называют областью действия этих локальных переменных, констант, типов и процедур. Константы, переменные, типы, описанные в блоке program, называются глобальными. Казалось бы, проще иметь дело вообще только с глобальными переменными, описав их все в program. Но использование локальных переменных позволяет системе лучше оптимизировать программы, делать их более наглядными и уменьшает вероятность появления ошибок.

47,48.Массив. Предположим, что программа работает с большим количеством однотипных данных. Скажем около ста разных целых чисел нужно обработать, выполнив над ними те или иные вычисления. Как вы себе представляете 100 переменных в программе? И для каждой переменной нужно написать одно и тоже выражение вычисления значения? Это очень неэффективно.

Есть более простое решение. Это использование такой структуры (типа) данных как массив. Массив представляет собой последовательность ячеек памяти, в которых хранятся однотипные данные. При этом существует всего одно имя переменной связанной с массивом, а обращение к конкретной ячейке происходит по ее индексу (номеру) в массиве.

Итак, массив – это именованная группа однотипных данных, хранящихся в последовательных ячейках памяти. Каждая ячейка содержит элемент массива. Элементы нумеруются по порядку, но необязательно начиная с единицы (хотя в языке программирования Pascal чаще всего именно с нее). Порядковый номер элемента массива называется индексом этого элемента.

Помним, все элементы определенного массива имеют один и тот же тип. У разных массивов типы данных могут различаться. Например, один массив может состоять из чисел типа integer, а другой – из чисел типаreal.

Индексы элементов массива обычно целые числа, однако могут быть и символами, а также описываться другими порядковыми типами. Т.е. для индекса можно использовать тип, в котором определена дискретная последовательность значений, и все эти значения можно пересчитать по порядку. Индексировать можно как константами и переменными, так и выражениями, результат вычисления которых дает значение перечислимого типа.

Если индекс массива может приобретать все допустимые значения определенного перечислимого типа, то при описании массива возможно задание имени типа вместо границ изменения индекса. При этом границами индекса будут первое и последнее значения в описании типа индекса. Границы изменения индексов могут задаваться с помощью ранее объявленных констант. Рекомендуется предварительно объявлять тип массива в разделе описания типов.

Массивы бывают следующих видов:

1. Одномерные – каждый элемент массива получает два индекса (

2. Многомерные – каждый элемент получает более 2-х индексов

49. Подпрограммы. Процедуры и функции: их отличие Подпрограммы. Функции - это процедуры особого характера, результатом работы которых является некоторое значение, подобное переменной.
Функция, как и процедура, может иметь список параметров, следующих за именем функции в круглых скобках. Но если имя процедуры используется только для ее вызова, то с именем функции связывается ее значение. На примере сложения двух целых чисел проиллюстрируем возможности Турбо Паскаля 7.0 по оформлению программ при помощи процедур и функций, а также рассмотрим различия между этими двумя подходами.

50. Формальные и фактические параметры. Их роль Параметры, указываемые при описании подпрограммы, называются формальными, а параметры, указываемые при вызове подпрограммы, – фактическими.

Список фактических параметров подпрограммы должен совпадать по количеству и типам со списком формальных параметров. Список формальных параметров необязателен и может отсутствовать (в этом случае будут отсутствовать и фактические параметры). При описании и вызове подпрограммы без параметров круглые скобки не указываются. Следующие подряд однотипные параметры можно объединять в подчиненные списки. Другими словами, можно указывать их через запятую, а за последним параметром – их тип. Параметры подпрограммы могут быть значениями, переменными, константами.

Параметры-значения передаются в подпрограмму через стек в виде их копий. Поэтому любые изменения таких параметров в теле процедуры ни как не отражаются на значениях внешних переменных. Параметры-значения используются для передачи в подпрограмму исходных данных, используемых для расчета. Такие параметры при описании подпрограммы не предваряются никакими зарезервированными словами. Для каждой из них указывается соответствующий тип данных.

Параметры-переменные указываются в описании подпрограммы после зарезервированного слова var. Действие зарезервированного слова var имеет силу до ближайшей точки с запятой. При вызове подпрограммы на месте параметра-переменной в качестве фактического параметра указывается переменная того же типа. При использовании параметра-переменной в подпрограмму передается сама переменная. Это позволяет вернуть в точку вызова подпрограммы измененные значения внешних переменных, которые были указаны в качестве параметров. Иными словами, изменения значений параметров-переменных в теле подпрограммы приводит также к изменению значений внешних переменных, указанных в качестве параметров при вызове подпрограммы.

Параметры-константы используются в подпрограммах. Если подпрограмма не должна менять передаваемое значение. В этом случае параметр передается в виде адреса той области памяти, в которой располагается константа. При передаче параметра-константы как параметра-значения (что, в принципе, возможно) быстродействие программы уменьшается. Перед именем параметра-константы указывается зарезервированное слово const, действие которого также распространяется до ближайшей точки с запятой.

50,51.51,52,53,54 Под нелинейными уравнениями понимаются алгебраические и трансцендентные уравнения вида где х- действительное число,- нелинейная функция, а под системой нелинейных уравнений - система вида не явяющаяся системой линейных алгебраич. уравнений; решением является N-мерный вектор. Уравнение и система могут трактоваться как нелинейное операторное уравнение с нелинейным оператором L, действующим из векторного конечномерного пространства в. Численными методами решения Н. у. наз. итерационные методы, определяемые переходом от уже известного приближения на n-й итерации к новому приближению и позволяющие при достаточно большом числе итераций найти решение уравнения с нужной точностью е. Важнейшие итерационные методы приближенного решения уравнения как относительно общего вида, так и специального вида, характерного для дискретных (сеточных) методов решения краевых задач для уравнений и систем уравнений с частными производными сильно эллиптич. типа, и являются предметом рассмотрения настоящей статьи. Нелинейные операторные уравнения, связанные с рассмотрением бесконечномерных пространств, являются весьма широким математич. понятием, содержащим в себе как частные случаи, напр., нелинейные интегральные уравнения и нелинейные краевые задачи. Численные методы их приближенного решения включают в себя также методы их аппроксимации конечномерными уравнениями; эти методы рассматриваются отдельно. Одним из важнейших методов решения уравнения является метод простой итерации, предполагающий возможность замены уравнения (3) эквивалентной системой где - элемент конечномерного нормированного пространства, а оператор Р, отображающий в, является оператором сжатия: Тогда в силу общего принципа сжатых отображений уравнение имеет единственное решение, итерационный метод простой итерации сходится при любом начальном приближении, и для погрешности на n-й итерации справедлива оценка Пусть нек-рое решение системы удается окружить шаром, и система рассматриваемая вместе с дополнительным условием эквивалентна системе (рассматриваемой вместе с условием причем неравенство справедливо для и любого. Тогда при выборе начального приближения из в методе тоже гарантируется сходимость к с оценкой погрешности Для дважды непрерывно дифференцируемых функций при наличии хорошего начального приближения к решению системы часто эффективным методом повышения точности является метод Ньютон а- Канторовича. В этом методе уравнение из, определяющее нек-рую поверхность, заменяется уравнением касательной плоскости к, проводимой через точку, где - ранее полученное приближение к решению При нек-рых дополнительных условиях метод Ньютона - Канторовича приводит к оценке погрешности типа где и - нек-рые константы. На каждой итерации этого метода необходимо решать систему линейных алгебраич. уравнений с матрицей при неизвестных Иногда эту матрицу сохраняют на нескольких итерациях, иногда производные заменяют разностными аппроксимациями. Метод Ньютона - Канторовича относится к группе методов линеаризации Другим методом из этой группы является метод секущих (Большое число итерационных методов (так наз. методов спуска) основано на замене задачи решения уравнения задачей минимизации нек-рого функционала I(и). Напр., в качестве I(и)можно взять В ряде случаев, когда исходные Н. у. сами являлись уравнениями Эйлера для задачи минимизации нек-рого функционала I(и), такая вариационная формулировка задачи является еще более естественной; операторы Lв подобных ситуациях являются градиентами функционалов I(и)и наз. потенциальными операторами Среди различных вариантов методов спуска можно назвать метод покоординатного спуска, различные градиентные методы и, в частности, метод наискорейшего спуска, метод сопряженных градиентов и др., а также и их модификации Ряд итерационных методов для решения уравнений описывающих нек-рое стационарное состояние, можно трактовать как дискретизации соответствующих нестационарных задач. Поэтому методы из этого класса называют установления методами Примером таких нестационарных задач являются задачи, описываемые системой обыкновенных дифференциальных уравнении: Введение дополнительной независимой переменной характерно и для метода дифференцирования по параметру. Его суть состоит во введении вспомогательного параметра выборе непрерывно дифференцируемых функций и замене системы на систему при система (олжна легко решаться, а функции должны совпадать с вообще говоря, определяет как функцию от, и искомое решение совпадает с. Если систему (продифференцировать по, то получится система обыкновенных дифференциальных уравнений Если на отрезке решить для нее задачу Коти с начальным условием, являющимся решением системы то будет найдено и нек-рое решение системы Дискретизация (10) по и приводит к численному методу для решения В методе продолжения по парапетру система (9) решается при причем при каждом указанном значении применяется нек-рый итерационный метод с начальным приближением, совпадающим с приближенно полученным решением системы при предыдущем значении. Оба названных метода по сути дела являются итерационными методами решения) со специальной процедурой нахождения хорошего начального приближения. Для случая систем большую трудность представляет задача локализации решения. Так как большинство итерационных методов сходится лишь при наличии достаточно хорошего приближения к решению, описанные выше два метода часто позволяют избавиться от необходимости непосредственной локализации решения. Для локализации также часто используются теоремы, основанные на топологич. принципах и монотонности операторов Для решения уравнени), являющихся простейшими частными число известных и применяемых на практике итерационных методов очень велико Помимо уже рассмотренных можно указать, напр., итерационные методы высших порядков (включающие в себя метод Ньютона как частный случай, и большое число итерационных методов, специально ориентированных на нахождение действительных или комплексных корней многочленов где - действительные или комплексные числа (Проблема локализации решения уравнения сводится к отысканию интервала, на концах к-рого непрерывная функция принимает значения разных знаков. Для случая, когда является многочленом, она теряет свою остроту, т. к. известны теоретич. оценки (и имеются методы нахождения всех корней с нужной точностью без задания хороших приближений к ним Итерационные методы для решения уравнений возникающих в сеточных аналогах нелинейных краевых задач для уравнений с частными производными, являются частными случаями методов решения сеточных систем (Одним из наиболее интенсивно применяемых методов решения вероятно, является модифицированный метод простой итерации, записываемый в виде Где уравнение (3) рассматривается как операторное уравнение в N-мерном евклидовом пространстве;, где S- обозначение множества линейных симметричных и положительных операторов, отображающих H в Н. Целесообразно изучение таких методов проводить не в пространстве H, а в пространстве Н B с новым скалярным произведением: где - скалярное произведение в Н. Если оператор Lтаков, что для него выполнены условия строгой монотонности и Липшиц-непрерывности
то уравнение (3) имеет единственное решение, метод (11) при подходящем выборе сходится при любом с оценкой погрешности: где (см. [13], [15]). В более общем варианте этой теоремы достаточно требовать выполнения (12), (13) для решения м и всех v, принадлежащих шару и принадлежности этому шару (см. [13]). В этом случае и константы, могут зависеть от R. Для проверки таких условий достаточно, напр., с помощью априорных оценок локализовать и, получая а затем, если (12) и (13) выполнены для любых ии vиз взять В (14) константу qможно уменьшить, если оператор Lдифференцируем и для его производной, представленной в виде суммы симметрия, части и кососимметрич.

Воспользуйтесь поиском по сайту: