Принцип калориметрических измерений

Определение тепловых эффектов различных процессов

 

Методические указания к лабораторной работе по курсу

Химия Модуль 2

 

 

Составители: Хохлачева Н.М.

Ильина Е.Б.

Мареичева Е.Е.

Cоловьева И.В.

 

Под редакцией Бабаевского П.Г.

 

Москва 2012

Нина Матвеевна Хохлачева

Елена Борисовна Ильина

Елена Евгеньевна Мареичева

Ирина Витальевна Соловьева

 

Под редакцией Петра Гордеевича Бабаевского

 

 

Определение тепловых эффектов различных процессов

 

 

Методические указания к лабораторной работе по курсу

Химия Модуль 2

 

 

СОДЕРЖАНИЕ

стр.

Введение.................................................. 4

1.Основные определения..................................... 5

1.1.Примеры теоретического расчета тепловых эффектов

физико-химических процессов............................... 9

2. Экспериментальное определение теплового эффекта

2.1. Принцип калориметрических измерений................... 11

2.2. Определение истинного изменения температуры............ 13

3. Лабораторные работы

3.1. Лабораторная работа 1. Определение удельной и молярной

теплоты растворения соли калориметрическим методом......... 16

3.2. Лабораторная работа 2. Определение теплоты образования

твердого раствора из двух твердых компонентов.................20

4. Контрольные вопросы..................................... 25

5.Задачи для самостоятельной работы....................... 26

Библиографический список................................... 32

 

 

ВВЕДЕНИЕ

 

Методические указания предназначены для лабораторного практикума по курсу Химия Модуль 2 при изучении темы: "Первый закон термодинамики и его приложение к физико-химическим процессам" для студентов направления 5516 "Материаловедение и технология новых материалов", 5535 "Защита окружающей среды" и специальностей 1104, 1106, 1107 технологии металлический материалов МАТИ-РГТУ им.К.Э. Циолковского.

Целью предлагаемой работы является ознакомление с калориметрическим методом определения тепловых эффектов термохимических процессов. Выполнение лабораторного практикума преследует цель обучения студентов навыкам: правильной постановки эксперимента, математической обработки результатов наблюдений, работы со справочными данными и с методами вычисления тепловых эффектов по закону Гесса. Для самостоятельной работы студентам предлагаются индивидуальные задачи.

 

 

Теоретическая часть

 

В основе изучения термохимических процессов лежит первый закон термодинамики:

Q = DU + W, (1)

где Q - количество сообщенной системе теплоты;

DU = U₂ – U₁ – приращение внутренней энергии;

W - суммарная работа, совершенная системой.

Во многих случаях единственной работой, совершаемой системой, является работа расширения:

W = p (V₂ – V₁) = p DV. (2)

Если процесс протекает при постоянном объеме, т.е. когда pDV=0, то

Q_V = DU. (3)

Таким образом, количество теплоты, сообщенной системе при постоянном объеме, равно приращению внутренней энергии системы.

В случае изобарного процесса можно записать:

U₂ – U₁ = Q_P – p(V₂ – V₁) или

Q_P =(U₂+ pV₂) – (U₁ + pV₁)

Введем функцию состояния энтальпию Н º U + pV,

и получим, что

Q_P = H₂ – H₁ = DH. (4)

Количество теплоты, сообщенной системе при постоянном давлении, равно приращению энтальпии системы.

Физико-химические процессы чаще проводятся при постоянном давлении, поэтому для расчетов изобарных тепловых эффектов используется изменение энтальпии DН, или сокращенно энтальпия процесса.

Тепловой эффект считают положительным для эндотермических процессов (DН > 0), что соответствует поглощению теплоты системой; и отрицательным − для экзотермических процессов (DН < 0), которые сопровождаются выделением теплоты.

Следствие первого закона термодинамики применительно к термохимическим процессам носит название закона Гесса:

тепловой эффект физико - химических процессов, протекающих при постоянном объеме или постоянном давлении не зависит от пути процесса (промежуточных стадий), а определяется только начальным и конечным состояниями системы (т.е. состоянием исходных веществ и продуктов реакции).

Иначе говоря,

если из данных исходных веществ можно различными путями получить заданные конечные продукты, то независимо от вида промежуточных стадий каждого пути, общий тепловой эффект для всех будет одним и тем же и равен алгебраической сумме теплот каждой стадии данного пути.

 

Термохимией называется раздел физической химии, в котором рассматривается применение закона Гесса (первого начала термодинамики) для вычисления тепловых эффектов различных физико-химических процессов: химических реакций, фазовых переходов, процессов растворения, гидратообразования, нейтрализации, разбавления растворов и др.

Теплота растворения твердого соединения с ионной кристаллической решеткой определяется суммой двух величин: теплотой разрушения кристаллической решетки (эта теплота затрачивается DН_плав>0) и теплотой сольватации (гидратации) ионов молекулами растворителя (экзотермический процесс DН_сольв < 0). Знак теплоты растворения может быть как положительным, так и отрицательным в зависимости от соотношения этих тепловых эффектов.

DН_раств. = DН_плав. + DН_{сольв.(гидрат)}. (5)

Теплота растворения зависит от концентрации химического соединения в растворе. Теплота, которая поглощается или выделяется при растворении одного моля вещества в таком количестве растворителя, чтобы образовался раствор с определенной моляльностью m, называется молярной интегральной теплотой растворения.

Теплотой разведения DН_{развед .} называют тепловой эффект сопровождающий разбавление раствора, содержащего один моль растворенного вещества, от концентрации m₂ до меньшей концентрации m₁. Согласно закону Гесса, она равна разности соответствующих интегральных теплот растворения:

DН_{развед.} = DН_m1 -- DН_m2. (6)

Теплоту образования кристаллогидрата соли DН_{гидрат.} так же можно определить основываясь на законе Гесса по справочным данным: интегральной теплоте растворения безводной соли DН_раств1 и интегральной теплоте растворения кристаллогидрата DН_раств.2.

DН_раств1 = DН_гидрат + DН_раств.2. (7) Образование кристаллогидрата рассматривается как промежуточная стадия перехода от безводной соли к раствору в больших количествах воды.

Теплота нейтрализации. При взаимодействии 1 моль сильной кислоты с сильным основанием в разбавленных водных растворах выделяется почти одинаковое количество теплоты:

Н⁺ + ОН⁻ = Н₂О_(ж); DН = − 55,9 кДж/моль.

Нейтрализация слабых кислот сильными основаниями или сильных кислот слабыми основаниями сопровождается одновременной диссоциацией слабого электролита. При этом выделяется или поглощается теплота диссоциации DН_дисс., которая зависит от теплоты, поглощаемой при распаде молекулы на ионы, и теплоты гидратации ионов молекулами воды. Теплота диссоциации может быть как положительной, так и отрицательной. Таким образом теплота нейтрализации слабых кислот и оснований DН_{нейтр.слаб.элек-та} складывается из двух величин: теплоты образования воды из ионов и теплоты диссоциации слабого электролита:

DН_{нейтр.слаб.эл-та} = − 55,9 + DН_дисс. (8)

 

Примеры решения задач

Пример 1. Вычислите тепловой эффект реакции образования аммиака (DН_х) из простых веществ 1/2 N₂ + 3/2 H₂ = NH₃,

по тепловым эффектам реакций:

2 Н₂ + O₂ = 2 H₂O_(ж); DН₁ = -571,68 кДж (I)

4 NH₃ + 3O₂ = 6 H₂O_(ж) + 2 N₂; DН₂ = -1530,28 кДж (II)

Р е ш е н и е: На основании закона Гесса с термохимическими уравнениями можно оперировать также, как и с алгебраическими. H₂O_(ж) и O₂ не входят в уравнение образования аммиака, поэтому, чтобы исключить их из уравнений (I) и (II), умножим уравнение (I) на три и вычтем из него уравнение (II):

6Н₂ + 3О₂ - 4 NH₃ - 3O₂ = 6 H₂O_(ж) - 6 H₂O_(ж) - 2 N₂ ; (III)

После преобразования уравнения (III) и деления его на четыре получим исходное уравнение: 3/2 H₂ + 1/2 N₂ = NH₃.

Отсюда в соответствии с законом Гесса для тепловых эффектов проведем аналогичные преобразования и получим:

DН_х = (3 DН₁ - DН₂ ) / 4 = [ 3 (-571,68) - (-1530,28) ] / 4 = - 46,19 кДж/моль

 

Пример 2. Теплота растворения соли Na₂SO_{3 (тв)} при 18^оС равна -11,30 кДж/моль. Теплота гидратации этой соли при переходе в Na₂SO₃ ^.7Н₂О _(тв) равна -58,16 кДж/моль. Определить теплоту растворения кристаллогидрата Na₂SO₃ ^.7Н₂О_(тв).

Р е ш е н и е: Согласно закону Гесса, образование кристаллогидрата рассматривается как промежуточная стадия перехода от безводной соли к раствору в больших количествах воды (см.уравнение 7).

DН_{раствNa2SO3 (тв)} = DН_гидрат + DН_{раствNa2SO3.7Н2О} .

Отсюда: DН_{раствNa2SO3.7Н2О} = -11,3 – (- 58,16) = 46,86 кДж/моль.

 

Пример 3. Теплоты нейтрализации NaOH и NH₄OH соляной кислотой соответственно равны -55.9 кДж/моль и -51,34 кДж/моль. Какова теплота диссоциации NH₄OH? Нейтрализация осуществляется в разбавленных растворах.

Р е ш е н и е: Согласно закону Гесса, теплота нейтрализации слабого основания DН_{нейтр.слаб.осн .} складывается из двух величин (см. уравнение 8): теплоты образования воды из ионов DН_{нейтр.сильн.осн.} и теплоты диссоциации слабого электролита.

Отсюда:

DН_дисс. = DН_{нейтр.слаб.осн.} – DН_{нейтр.сильн.осн.} = -51,34 – (-55.9) = 4,56кДж/моль.

Практическая часть

Принцип калориметрических измерений

 

Экспериментальное определение тепловых эффектов проводят в специальном приборе -- калориметре (рис.1). Он позволяет определять тепловые эффекты процессов растворения, гидратообразования, химических реакций и др., протекающих при температурах близких к комнатным (20 – 50^оС).

4

5 -

3

2

 

1

 

 

 

 

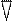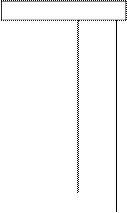
Рис.1. Лабораторный калориметр:

1 – калориметрический сосуд; 2 – крышка; 3 – мешалка; 4 – термометр; 5 – отверстие для введения исследуемого вещества.

 

Калориметрический сосуд состоит из воздушного термостата и помещенного в нем калориметрического стакана. Калориметрический сосуд может быть металлический, фарфоровый или стеклянный. Изолирующей системой является воздушная оболочка, которая образуется между другим сосудом и крышкой. Внутренний калориметрический сосуд устанавливается в калориметре на асбестовых или пластмассовых подставках. В крышке имеются отверстия для термометра, мешалки, введения исследуемого вещества. Для уменьшения потерь тепла в окружающую среду изменение температуры при взаимодействии веществ в калориметрическом сосуде не должно превышать 2 – 3^о и реакция должна протекать быстро.

При калориметрических опытах величина и знак теплового эффекта Q процесса в калориметре определяются по изменению температуры калориметра Dt. Давление в калориметрической системе остается постоянным (равным атмосферному), поэтому тепловой эффект Q_p равен изменению энтальпии процесса DН. Знак теплового эффекта процесса будет обратным знаку Dt (т.к. поглощение тепла сопровождается уменьшением температуры, а выделение тепла - ее повышением).

Уравнение теплового баланса в калориметре можно записать в виде:

Q_p = DН = - å (c_{p i} g_i) Dt, (9)

где g_i - масса исследуемого раствора в калориметре, а также массы вспомогательных устройств калориметрической системы (стакана, мешалки, термометра и т.д.);

c_{p i} – удельные теплоемкости исследуемого раствора и вспомогательных устройств калориметрической системы;

Dt – изменение температуры процесса, с учетом поправки на теплообмен с окружающей средой (истинное изменение температуры опыта).

Теплоемкость калориметрической системы, участвующей в теплообмене, постоянна для каждого эксперимента, и ее называют постоянной калориметра К. По физическому смыслу, константа калориметра К численно равна количеству тепла, необходимого для нагревания всех частей калориметра на один градус.

Уравнение теплового баланса можно записать с учетом этого, по-иному:

Q_p = DН = - (с_р-ра g_р-ра + К) Dt [Дж], (10)

где с_р-ра – удельная теплоемкость исследуемого раствора [Дж/ г К];

g_р-ра - масса исследуемого раствора [ г ];

К - константа калориметра [Дж/ К].

Таким образом, для вычисления исследуемого теплового эффекта необходимо предварительно найти значение постоянной калориметра К.

Экспериментальная задача сводится к измерению истинного скачка температуры, который происходит вследствие выделения или поглощения теплоты в результате опыта.

 

Определение истинного изменения температуры в калориметре при термохимическом процессе.

Расчет величины Dt с учетом теплообмена с окружающей средой может быть проведен графически.

Весь калориметрический процесс можно разделить на три периода:

1) начальный период: калориметрический стакан прибора (рис.1) заполняют калориметрической жидкостью (например, дистиллированной водой) и в течении 5-8 минут измеряют температуру в калориметрической системе до начала изучаемого процесса, записывая показания термометра через одну минуту.

2) главный период: проводят процесс, тепловой эффект которого определяется (например, растворяют навеску соли). Температуру непрерывно продолжают отсчитывать через те же промежутки времени. За счет выделения или поглощения тепла в процессе происходит резкое изменение температуры.

3) конечный период: по завершении главного периода вновь устанавливается равномерный ход выравнивания температуры, и в течение еще приблизительно 15 минут производят замеры температуры с тем же интервалом.

На основании экспериментальных данных строят график изменения температуры от времени в ходе калориметрического опыта. На оси абсцисс откладывают время в масштабе 1 мин=0.5см; на оси ординат температуру, выбор масштаба которой зависит от величины Dt. При Dt £ 1^o выбирают масштаб 1^о = 10 см; при Dt ³1^о выбирают масштаб 1^о = 5 см.

Типичный вид температурной кривой правильно поставленного калориметрического опыта при измерении эндотермического эффекта показан на рис.2.

Рис.2. Определение изменения температуры в ходе калориметрического опыта

 

После того как на график нанесены все экспериментальные точки, получается кривая ABCD. Участок АВ соответствует начальному периоду эксперимента, ВС - главный период; CD - конечный период. Чтобы определить изменение температуры Dt, не искаженное теплообменом с окружающей средой, происходящим в течение главного периода, проводят геометрическое построение. Для этого верхнюю и нижнюю точки главного периода (точки В и С) сносят на ось ординат, получают точки n и m. Через середину отрезка nm, точку К, проводят прямую параллельную оси абсцисс до пересечения с экспериментальной кривой в точке f. Из точки f восстанавливают перпендикуляр к оси абсцисс. Продолжение линии АВ (начального периода) и CD (конечного периода) до пересечения с перпендикуляром позволяет получить отрезок EF, который показывает истинное изменение температуры в калориметрическом опыте. Отрезок EF, равный Dt, выражают в градусах в соответствии с масштабом. Для экзотермического процесса Dt > 0 и для эндотермического - Dt < 0.

Характер линии ВС зависит от условий протекания теплового процесса (например, размешивания). Наклон линий АВ и CD зависит от характера теплообмена с окружающей средой.

 

 

лабораторная Работа 1

Определение удельной и молярной теплоты растворения соли

Цель работы:

1. Ознакомиться с калориметрическим методом определения тепловых эффектов.

2. Определить константу калориметра.

3. Определить теплоту растворения соли.

 

Удельной теплотой растворения называют тепловой эффект, сопровождающий растворение твердого вещества в жидкости и отнесенный к 1 г растворенного вещества. Молярной теплотой растворения называют тепловой эффект, отнесенный к одному молю растворяемого вещества.

Теплота растворения зависит от концентрации раствора и интегральной теплотой растворения называют тепловой эффект растворения одного моля (молярная) или одного грамма (удельная) вещества в данном количестве растворителя.

 

Порядок выполнения работы

1. Определение константы калориметра.

Для вычисления теплового эффекта изучаемого процесса растворения (см.уравнение 10) необходимо предварительно определить постоянную калориметра К. Эту величину определяют по понижению температуры при растворении в воде соли KCl. Зная молярную интегральную теплоту растворения этой соли, рассчитывают К по уравнению теплового баланса для 1 моля растворенного вещества:

DН_m^o = - [(G + ) c_p-pa + K ] , [Дж/моль] (11)

где G – масса воды в калориметре, [ г ];

g – масса навески соли KCl, [ г ];

с_р-ра = 4,1 [Дж/ г К] – удельная теплоемкость водного раствора (теплоемкости разбавленных водных растворов неорганических солей практически одинаковы);

М_KCl - молекулярная масса соли KCl;

Dt - истинное изменение температуры в процессе растворения. которое определяется графически;

DН_m^o - значение молярной интегральной теплоты растворения соли KCl, соответствующее концентрации полученного раствора, находят по справочным таблицам. Предварительно необходимо рассчитать моляльность m полученного раствора (число молей вещества на 1000 г воды):

m = (12)

и по справочнику [3] (табл.31) для данной концентрации раствора KCl найти значение молярной интегральной теплоты растворения этой соли DН_m^o.

 

Проведение опыта:

1) Взвесить на технических весах 5 г измельченного КСl.

2) В калориметрический стакан отмерить цилиндром 150 мл дистиллированной воды.

3) Собрать прибор, как указано на рис.1 (см. 2.1. стр. 11) и приступить к выполнению калориметрических измерений. В течение начального периода, при непрерывном перемешивании дистиллированной воды, записывать показания термометра каждую минуту. В начале главного периода высыпать в калориметрический стакан через специальное отверстие в крышке калориметра взвешенную навеску соли и продолжить измерение температуры до конца опыта, не прекращая перемешивание раствора.

4) Полученные результаты записывать по форме в таблицу 1.

Таблица 1.

Изменение температуры с течением времени при протекании процесса растворения соли KCl.

 

t, мин

toC

начальный период

главный и конечный период

 

5) По полученным данным построить график зависимости температуры от времени, как указано на рис.2. Определить графически Dt процесса растворения соли KCl (см. стр.11).

6) Рассчитать константу калориметра К [ Дж/К ] по уравнению (11).

 

2. Определение удельной и молярной теплоты растворения исследуемой соли.

Последовательность эксперимента:

1) Взвесить на технических весах 5 г исследуемой соли по заданию преподавателя.

2) Далее опыт провести, как указано в разделе 2.1 пункты (2 – 3).

3) Результаты опыта записывать в таблицу 2.

 

Таблица 2.

Изменение температуры с течением времени при протекании процесса растворения исследуемой соли.

 

t, мин

toC

начальный период

главный и конечный период

 

 

4) По полученным данным построить график зависимости температуры от времени, как указано на рис.2. Определить графически Dt процесса растворения исследуемой соли.

5) Рассчитать удельную теплоту растворения исследуемой соли по уравнению:

 

q = - [(G + ) c_p-pa + K ] Dt / , [Дж / г ] (13)

где q - удельная теплота растворения соли;

G – масса воды в калориметре, [ г ];

g – масса навески исследуемой соли, [ г ];

с_р-ра = 4,1 [Дж/ г К] – удельная теплоемкость исследуемого водного раствора;

К – константа калориметра, вычисленная в предыдущем опыте;

Dt - истинное изменение температуры в процессе растворения исследуемой соли, которое определяется графически.

6) Рассчитать интегральную молекулярную теплоту растворения исследуемой соли по уравнению:

 

DН^о_{m экспер.} = q М_соли, [Дж/моль] (14)

где М_соли – молекулярная масса исследуемой соли.

7) Сравнить полученную экспериментальную величину молекулярной теплоты растворения DН^о_{m экспер} с табличной величиной DН^о_{m табл} (справочник [3] табл.31).

Рассчитать ошибку эксперимента по уравнению:

В,% = 100 % ^. (DН^о_{m табл} − DН^о_{m экспер}) / DН^о_{m табл} , (15)

где В,% - относительная ошибка эксперимента %.

 

Лабораторная Работа 2

Определение теплоты образования твердого раствора из двух твердых компонентов

 

Цель работы:

1. Ознакомиться с калориметрическим методом определения тепловых эффектов.

2. Определить константу калориметра.

3. Определить теплоту растворения твердого раствора.

4. Рассчитать теплоту образования твердого раствора.

 

В работе предлагается определить теплоту образования твердого раствора KCl ^. KBr из хлорида калия (KCl) и бромида калия (KBr), которые неограниченно растворимы друг в друге как в жидком, так и в твердом состояниях.

Величина и знак теплового эффекта при образовании твердого раствора из индивидуальных кристаллических веществ позволяют судить о характере взаимодействия их в твердом растворе.

Теплоту образования твердого раствора DН^о_{обр.тв.р.} из кристаллических компонентов непосредственно в калориметрах определить нельзя, так как скорость процесса мала. Однако величину DН^о _{обр.тв.р.} можно определить косвенным путем. Для этого следует определить теплоты растворения твердого раствора (DН^о_KCl.KBr) и механической смеси того же состава (DН^о_{KCl + KBr}). По закону Гесса:

DН^о _{обр.тв.р.} = DН^о_{KCl + KBr} - DН^о_KCl.KBr (16)

 

Порядок выполнения работы

1, Определение константы калориметра.

Для вычисления теплового эффекта изучаемого процесса растворения необходимо предварительно определить постоянную калориметра К. (См. работу 1 стр.14)

 

2. Определение удельной и молярной теплоты растворения твердого раствора.

Проведение опыта:

1) Взвесить на технических весах 5 г измельченного исследуемого твердого раствора KCl ^. KBr.

2) В калориметрический стакан отмерить цилиндром 150 мл дистиллированной воды.

3) Собрать прибор, как указано на рис.1 и приступить к выполнению калориметрических измерений (см. 2.1. стр. 11). В течение начального периода, при непрерывном перемешивании дистиллированной воды, записывать показания термометра каждую минуту. В начале главного периода высыпать в калориметрический стакан через специальное отверстие в крышке калориметра взвешенную навеску твердого раствора и продолжить измерение температуры до конца опыта, не прекращая перемешивание раствора.

4) Полученные результаты записывать по форме в таблицу 3.

Таблица 3.

Изменение температуры с течением времени при протекании процесса растворения твердого раствора.

 

t, мин

toC

начальный период

главный и конечный период

 

5) По полученным данным построить график зависимости температуры от времени, как указано на рис.2. Определить графически Dt процесса растворения твердого раствора (см. стр.11).

6) Рассчитать удельную теплоту растворения твердого раствора по уравнению:

q _KCl.KBr = - [(G + ) c_p-pa + K ] Dt / , [Дж / г] (17)

 

где q _KCl.KBr - удельная теплота растворения твердого раствора;

G – масса воды в калориметре, [ г ];

g – масса навески твердого раствора, [ г ];

с_р-ра = 4,1 [Дж/ г К] – удельная теплоемкость исследуемого водного раствора;

К – константа калориметра, вычисленная в предыдущем опыте;

Dt - истинное изменение температуры в процессе растворения исследуемой соли, которое определяется графически.

7) Рассчитать молекулярную теплоту растворения твердого раствора

 

DН^о _KCl.KBr = q _KCl.KBr М _KCl.KBr, [Дж/моль] (18)

где М_KCl.KBr – молекулярная масса исследуемого твердого раствора. Эту величину определяют следующим образом. Твердый раствор состоит из 50 мас% KCl и 50 мас% KB r и молекулярная масса твердого раствора рассчитывается по уравнению:

 

, (19)

 

где n_KCl и n_KBr - числа молей KCl и KBr в навеске;

М_KCl и M_KBr - соответствующие молекулярные массы;

g_KCl.KBr – масса навески твердого раствора,

 

3. Расчет теплоты образования твердого раствора.

1) Рассчитать теплоту растворения механической смеси (50%KCl+50% KBr) по уравнению:

DН^о_{KCl + KBr} = (n_KCl DН^о_m,KCl + n_KBr DН^о_m,KBr) / (n_KCl+ n_KBr), (20)

где DН^о_m,KCl и DН^о_m,KBr - интегральные молярные теплоты растворения KCl и KBr соответственно. Их значения находят по справочным таблицам. Т.к. теплота растворения зависит от концентрации соединения в растворе, необходимо рассчитать моляльность m полученного раствора (число молей вещества на 1000 г воды):

m = (21)

и по справочнику [3] (табл.31) найти значение DН_m^o молярной интегральной теплоты растворения данной соли, соответствующее концентрации полученного раствора.

2) Рассчитать теплоту образования твердого раствора DН^о _{обр.тв.р.} по уравнению (16).

3) Сделать выводы по знаку теплоты образования твердого раствора.

 

 

Контрольные вопросы

 

1. Какими функциями определяется количество теплоты, переданное в изохорических и изобарических процессах?

2. Дайте определение эндотермических и экзотермических процессов.

3. Сформулируйте закон Гесса.

4. В чем заключается физический смысл теплоты растворения твердого вещества в жидкости?

5. Что называется удельной, молекулярной интегральной теплотой растворения? Каковы их единицы измерения?

6. Что называется теплоемкостью вещества, какова ее размерность? Какие виды теплоемкости используются для термодинамических расчетов?

7. Какова зависимость теплового эффекта от температуры?

8. Как определить истинное изменение температуры в опыте, неискаженное теплообменом с окружающей средой?

9. Что называется константой калориметра? Какова ее размерность? От каких величин она зависит?

10. Как определить тепловую постоянную калориметра?

11. Каковы причины ошибок в данной работе? Как определить абсолютную и относительную ошибки эксперимента?

 

Задачи для самостоятельной работы.

 

1. Вычислите количество теплоты, которое требуется на разложение 1 моль безводного карбоната натрия

Na₂CO₃ (к) = Na₂O (к) + CO₂ (г)

если известно, что

Na₂CO₃ (к) + SiO₂ (к) = Na₂SiO₃ (к) + CO₂ (г); DН⁰ = 81,04 кДж

Na₂О (к) + SiO₂ (к) = Na₂SiO₃ (к); DН⁰ = - 243,17 кДж

 

2. Определите энтальпию разложения Н₂O₂ на воду и кислород по уравнению Н₂O₂ = H₂O(ж) + 1/2O₂ (г), используя следующие данные:

SnCl₂ (р) + 2HCl (р) + Н₂O₂ (p) = SnCl₄ (р) + 2H₂O (ж); DН⁰ = - 393,3 кДж

SnCl₂ (р) + 2HCl (р) + 1/2O₂ (г) = SnCl₄ (р) + H₂O (ж); DН⁰ = - 296,6 кДж

 

3. Рассчитать теплоту образования жидкого сероуглерода по предполагаемому уравнению: С_{(графит)} + 2S_(мон) = CS₂ (ж) по следующим данным:

S_(мон) + О₂(г) = SO₂(г); DН⁰ = - 296,9 кДж

CS₂ (ж) + 3О₂(г) = СО₂(г) + 2SO₂(г); DН⁰ = - 1109,0 кДж

С_{(графит)} + О₂(г) = СО₂(г); DН⁰ = - 393,5 кДж

 

4. Вычислите изменение энтальпии (298 К) в реакции

2Н₂S (г) + SO₂ (г) = 3S (к) + 2H₂O (г), если

Н₂S (г) + 3/2О₂ (г) = H₂O (ж) + SO₂ (г); DН⁰ = - 561,1 кДж

S _(k) + O₂ = SO_2(г); DН⁰ = –296,2 кДж/моль.

 

5. Вычислите энтальпию образования водного раствора азотистой кислоты по уравнению 1/2H₂(г) + 1/2N₂(г) + О₂ (г) = HNO₂ (p), воспользовавшись энтальпиями (298 К) следующих реакций:

NH₄NO₂ (p) = N₂ (г) + 2H₂O (ж); DН⁰ = - 320,0 кДж

NH₃ (р) + HNO₂ (p) = NH₄NO₂ (p); DН⁰ = - 37,7 кДж

NH₃ (р) = ½ N₂ (г) + 3/2 H₂ (г) DН⁰ = + 84,9 кДж

H₂ (г) + ½ О₂ (г) = H₂O (ж); DН⁰ = - 285,8 кДж

6. Даны тепловые эффекты реакций:

С + О₂ = СО₂ ; DН⁰ = - 405,8 кДж

СО + 1/2О₂ = СО₂; DН⁰ = - 284,5 кДж

Рассчитать тепловой эффект реакции:

С_{(графит)} + ½ О₂ = СО

 

7. Вычислите стандартную энтальпию образования жидкого метилового спирта С (к) + 2Н₂ (г) + ½ О₂ (г) = СН₃ОН (ж), воспользовавшись следующими данными:

Н₂ (г) + ½ О₂ (г) = H₂О (ж); DН⁰ = - 285,8 кДж

С (к) + О₂ (г) = СО₂ (г); DН⁰ = - 393,7 кДж

СН₃ОН (ж) + 3/2 О₂ (г) = СО₂ (г) + 2H₂О (ж); DН⁰ = - 715,0 кДж

 

8. Вычислите изменение энтальпии DН⁰ в процессе превращения диметилового эфира в этиловый спирт:

СН₃ОСН₃ (г) = СН₃СН₂ОН(г),

если

СН₃ОСН₃ (г) + 3О₂ (г) = 2СО₂ (г) + 3H₂О (г); DН⁰ = - 1454 кДж

СН₃СН₂ОН(г) + 3О₂ (г) = 2СО₂ (г) + 3H₂О (г); DН⁰ = - 1402 кДж

 

9. Определите энтальпию гидратации карбоната натрия

Na₂CO₃ (к) + 10 H₂О (ж) = Na₂CO₃ 10 H₂О (к)

если известны энтальпии растворения безводной соды

Na₂CO₃ (кр.) + ∞ H₂О (ж) = Na₂CO₃ (р-р); DН⁰ = - 24,6 кДж

и кристаллогидрата

Na₂CO₃ 10 H₂О (к) + (∞−10)H₂О (ж) = Na₂CO₃ (р-р); DН⁰ = + 66,6 кДж

 

10. Даны тепловые эффекты реакций:

С + О₂ = СО₂ ; DН⁰ = - 405,8 кДж

СО + 1/2О₂ = СО₂; DН⁰ = - 284,5 кДж

Н₂ + 1/2О₂ = Н₂О_(г); DН⁰ = - 246,8 кДж

Используя необходимые уравнения, рассчитать тепловой эффект реакции:

С + Н₂О_(г) = СО + Н₂

 

11. Рассчитайте энтальпию реакции

F(г) + Li(г) = F ^- (г) + Li ⁺ (г)

если

F(г) + е ^- = F ^- (г); D Н⁰_{сродства} = - 322 кДж

Li(г) = Li ⁺ (г) + е ^- ; D Н⁰_иониз = 520 кДж

 

12. Даны тепловые эффекты реакций:

С + О₂ = СО₂ ; DН⁰ = - 405,8 кДж

Н₂ + 1/2О₂ = Н₂О_(г); DН⁰ = - 246,8 кДж

Рассчитать тепловой эффект реакции:

С + 2 Н₂О_(г) = СО₂ + 2 Н₂.

 

13. Даны тепловые эффекты реакций:

С + О₂ = СО₂ ; DН⁰ = - 405,8 кДж

СО + 1/2О₂ = СО₂; DН⁰ = - 284,5 кДж

Рассчитать тепловой эффект реакции:

2СО = СО₂ + С.

 

 

14. На основании приведенных ниже данн

Поделиться:

Воспользуйтесь поиском по сайту: