 |
Практические расчеты на устойчивость
|
|
|
|
Для сжатых стержней кроме условия прочности должно быть удовлетворено также условие устойчивости, которое можно выразить неравенством
 ,
| (8.18) |
где 
- допускаемое напряжение при расчете на устойчивость.
Ослабление сечений стержня заклепками или болтами в металлических конструкциях, врубками — в деревянных происходит не по всей его длине, а лишь на отдельных небольших участках. Сопротивление же стержня выпучиванию зависит от жесткости стержня на всем его протяжении. Поэтому местные ослабления практически не влияют на величину критической силы.
Допускаемое напряжение при расчетах на устойчивость назначается с запасом против критического напряжения, т.е. выражается формулой
 ,
| (8.19) |
где 
— нормативный (или требуемый) коэффициент запаса устойчивости, значения которого принимаются различными для различных материалов и зависят от гибкости стержня.
Коэффициент запаса устойчивости принимается более высоким, чем коэффициент запаса прочности. Это вызывается рядом обстоятельств, практически не поддающихся учету (начальная кривизна стержня, нецентральное действие нагрузки и др.), которые уменьшают критическую нагрузку, но почти не влияют на прочность конструкции.
Выразим допускаемое напряжение через допускаемое напряжение 
, принимаемое при расчетах на прочность:
 ,
| (8.20) |
где 
— коэффициент уменьшения основного допускаемого напряжения для сжатых стержней (коэффициент продольного изгиба).
Значения коэффициента приведены в таблице 8.1. Они зависят от материала стержня и его гибкости.
Условие устойчивости (8.18) после замены через с помощью формулы (8.20) принимает вид
 .
| (8.21) |
Кроме условия устойчивости сжатые стержни должны удовлетворять и условию прочности
|
|
|
 .
| (8.22) |
Таблица 8.1
Гибкость
| Коэффициенты для различных материалов
| ||||
| Сталь Ст 3,4,2, ОС | Сталь Ст5 | Сталь СПК | чугун | дерево | |
| 1,00 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75 0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19 0,17 0,16 | 1,00 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70 0,62 0,51 0,43 0,36 0,33 0,29 0,26 0,24 0,21 0,19 0,17 0,16 0,14 0,13 | 1,00 0,97 0,95 0,91 0,87 0,83 0,79 0,72 0,65 0,55 0,43 0,35 0,30 0,26 0,23 0,21 0,19 0,17 0,15 0,14 0,13 | 1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,20 0,16 - - - - - - - - - - - | 1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,10 0,9 0,8 |
Подбор сечения сжатых стержней представляет собой более сложную задачу, чем растянутых стержней [2]. Это объясняется тем, что величина , входящая в расчетную формулу, зависит от размеров и формы поперечного сечения и поэтому заранее не может быть назначена. Ввиду этого решение обычно проводится путем последовательных попыток.
Рассмотрим два вида расчета на устойчивость сжатых стержней - проверочный и проектировочный [3].
Проверочный расчет сжатых стержней. Порядок проверочного расчета на устойчивость при использовании таблицы коэффициентов следующий:
1) исходя из известных размеров и формы поперечного сечения, определяем наименьший осевой момент инерции 
, площадь 
, вычисляем минимальный радиус инерции
и гибкость
;
2) по таблице находим коэффициент и вычисляем допускаемое напряжение на устойчивость по формуле
;
3) сравниваем действительное напряжение 
с допускаемым напряжением 
.
Пример 8.1. Проверить на устойчивость сжатую деревянную колонну
Рис. 8.7. Расчетная схема
колонны
|
(рис. 8.7) квадратного поперечного сечения (
) длиной 
, если основное допускаемое напряжение 
, а сжимающая сила 
.
Определяем следующие величины:
площадь -
;
момент инерции -
;
радиус инерции -
;
приведенную длину -
;
гибкость -
|
|
|
.
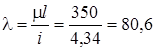По таблице 8.1 интерполяцией находим, что
.
Тогда
;
.
Так как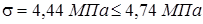 
, то устойчивость колонны обеспечена.
Проектировочный расчет. В расчетной формуле на устойчивость
, или 
,
имеются две неизвестные величины - коэффициент и искомая площадь поперечного сечения. Поэтому при подборе сечений приходится пользоваться методом последовательных приближений, варьируя величину коэффициента . Обычно в первой попытке берут 
. Принимая какое-либо из этих значений 
, определяют требуемую площадь и подбирают сечение. Подобранное сечение проверяют и устанавливают фактическое значение 
. Если значительно отличается от , то напряжение отличается от допускаемого. Тогда следует повторить расчет, т.е. сделать вторую попытку, приняв среднее по величине значение между и :
.
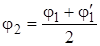В результате второй попытки устанавливают 
. Если требуется третья попытка, то
и т.д. Обычно при подборе сечений требуется не более двух-трех попыток.
Пример 8.2. Подобрать по сортаменту двутавровое поперечное сечение стержня длиной 5 м, находящегося под действием центральной сжимающей нагрузки 320 кН. Оба конца стержня защемлены. Материал - Ст 3. Основное допускаемое напряжение 
.
Определяем расчетную длину стержня:
.
Подбираем поперечное сечение путем последовательных приближений.
Первая попытка: принимаем =0,5; требуемая площадь поперечного сечения
.
По сортаменту подбираем двутавр № 27 с площадью 
и минимальным радиусом инерции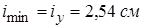 
. Гибкость стержня
.
По таблице 8.1 при линейной интерполяции
.
Перейдем ко второму приближению, приняв 
.
Необходимая площадь поперечного сечения стержня
.
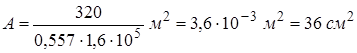По сортаменту подбираем двутавр № 24 а с площадью 
и минимальным радиусом инерции 
. Гибкость стержня
.
По таблице 8.1 находим коэффициент :
.
Переходим к третьему приближению, приняв
.
Вычисляем необходимую площадь:
.
По сортаменту подбираем двутавр № 24 с площадью 
и минимальным радиусом инерции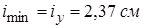 
. Гибкость стержня
.
Для 
коэффициент
.
Вычисляем напряжение:
.
Перенапряжение составляет
.
Окончательно принимаем для стержня двутавр № 24.
Пример 8.3. Определить величину допускаемой нагрузки на деревянную стойку высотой и сечением 
. Концы стойки закреплены шарнирно. 
.
Решение. Площадь сечения стойки 
.
|
|
|
Наименьший момент инерции сечения стойки
.
Минимальный радиус инерции
.
Гибкость стойки
.
По таблице 8.1 для 
интерполированием находим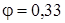 
.
Допустимая сила равна напряжению, умноженному на площадь сечения и на коэффициент , т.е.
.
Пример 8.4. Определить допускаемую нагрузку на стойку двутаврового профиля № 30 а (сталь Ст. 3), защемленную в основании и шарнирно закрепленную верхним концом. Высота стойки , коэффициент запаса устойчивости 
; 
.
Решение. Из таблицы сортамента для заданного двутаврового профиля № 30а выписываем необходимые данные для решения задачи: 
; 
; наименьший радиус инерции 
.
Определяем гибкость стойки:
,
следовательно, критическую нагрузку на стойку определяем по формуле Эйлера
,
где 
.
Пример 8.5. Стержень прямоугольного сечения закрепляется таким образом, что в плоскости наибольшей жесткости концы его могут свободно поворачиваться, а в плоскости наименьшей жесткости поворот концевых сечений исключен (рис. 8.8).
Определить допускаемое значение центрально приложенной сжимающей силы, если 
. Материал стержня - сталь 45, 
.
Решение. В рассматриваемом случае закрепление концов стержня в главных плоскостях инерции различно, поэтому расчет следует вести исходя из опасности потери устойчивости вокруг той из главных осей, относительно которой гибкость стержня максимальна.
Определяем радиусы инерции сечения:
;
.
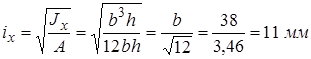Рис. 8.8. Расчетная схема стержня.
|
Определяем значение гибкости относительно главных осей 
; 
(концы стержня могут поворачиваться):
;
; 
(концы стержня не могут поворачиваться):
.
Таким образом, опаснее потеря устойчивости в плоскости наибольшей жесткости, т.е. 
.
Определяем допускаемое значение сжимающей силы. Расчет ведем по формуле Эйлера, так как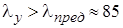 
:
.
Пример 8.6. Проверить на устойчивость сжатую стойку трубчатого сечения (рис. 8.9) из хромомолибденовой стали (
, 
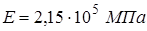), если требуемый коэффициент запаса устойчивости 
.
Решение. Определяем предельную гибкость стойки:
.
Для определения гибкости стойки вычисляем момент инерции ее поперечного сечения (в данном случае любая центральная ось главная и все центральные моменты инерции равны между собой)
|
|
|
;
затем площадь сечения
Рис. 8.9. Расчетная схема стойки
|
и радиус его инерции
.
Коэффициент приведения длины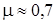 
(см. рис. 8.9).
Гибкость стойки
.
Так как гибкость стойки больше предельной 
, то критическую силу определяем по формуле Эйлера
.
Определяем коэффициент запаса устойчивости и сравниваем с заданным:
.
Пример 8.7. Определить допускаемую нагрузку для стойки из стали Ст3 (рис. 8.10), 
. Принять, что швеллеры, из которых состоит стойка,
Рис. 8.10. Расчетная схема стойки
|
надежно связаны между собой и сечение работает как монолитное. Расстояние с между швеллерами выбрать из условия равноустойчивости стойки во всех направлениях.
С каким коэффициентом запаса устойчивости работает стойка при нагрузке, равной допускаемой?
Решение. Равноустойчивость стойки во всех направлениях будет обеспечена при равенстве моментов инерции относительно осей х и у. Момент инерции сечения относительно оси х не зависит от расстояния с и определяется непосредственно на основе табличных данных:
,
где 
-момент инерции одного швеллера по ГОСТ 8240-72. Момент инерции относительно оси у
где 
- момент инерции швеллера относительно собственной главной центральной оси 
; 
- площадь сечения одного швеллера.
Условие равноустойчивости
;
подставляя числовые значения, получаем
,
откуда 
;
.
Определяем допускаемую нагрузку:
Гибкость стойки
,
где 
(по ГОСТ 8240-72); 
(интерполируя данные таблицы 8.1).
;
.
Определяем коэффициент запаса устойчивости, который соответствует таблице для данных материала и гибкости:
.
Так как гибкость стойки меньше предельной (для стали Ст3 
), то 
определяем по эмпирическому соотношению
;
.
8.2. Контрольные вопросы
1. В чем заключается явление потери устойчивости сжатого стержня?
2. Что называется критической силой и критическим напряжением?
3. Какое дифференциальное уравнение из теории изгиба лежит в основе вывода формулы Эйлера?
4. Что называется гибкостью стержня?
5. Какой вид имеет формула Эйлера, определяющая величину критической силы? Выведите эту формулу.
6. Как влияют жесткость 
поперечного сечения и длина 
стержня на величину критической силы?
7. Какой момент инерции обычно входит в формулу Эйлера? Возможны ли здесь исключения?
8. Что представляет собой коэффициент приведения длины и чему он равен при различных условиях закрепления концов сжатых стержней?
9. Как устанавливается предел применимости формулы Эйлера?
10. Что называется предельной гибкостью? Выведите выражение, определяющее предельную гибкость.
|
|
|
11. Какой вид имеет формула Ясинского для определения критических напряжений и при каких гибкостях она применяется для стержней из стали Ст3?
12. Как определяется критическая сила по Ясинскому?
8. Какой вид имеет график зависимости критических напряжений от гибкости для стальных стержней?
14. Если сжатый стержень ошибочно рассчитан по формуле Эйлера в области ее неприменимости, опасна ли эта ошибка или она приведет к перерасходу материала на изготовление стержня?
15. Какой вид имеет условие устойчивости сжатого стержня? Какая площадь поперечного сечения стержня подставляется в это условие?
16. Что представляет собой коэффициент , как определяется его значение? Как производится проверка стержней на устойчивость с его помощью?
17. Как подбирается сечение стержня при расчете на устойчивость?
|
|
|
