Метод прямоугольного треугольника

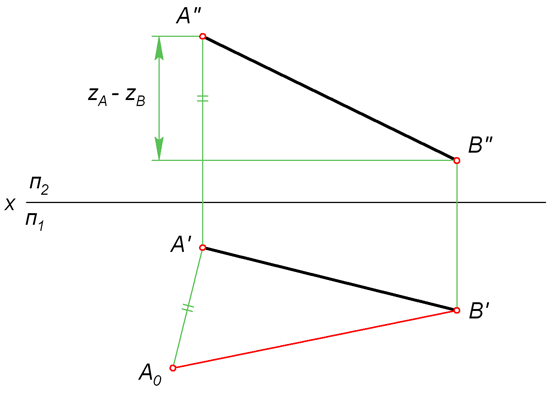
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

 

17. Сушность способа замены плоскостей

Этот способ заключается в том, что заданную систему плос­костей проек­ций заменяют новой системой так, что предмет (прямая или плоскость), не изменяя своего положения в про­странстве, оказывается в частном положении относительно новой системы плоскостей проекций. Плоскости проекций обра­зуют новую ортогональную систему.

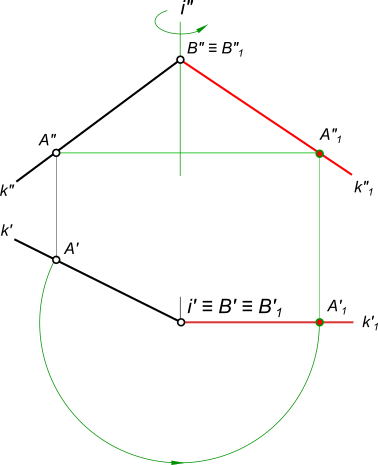
18. Вращение вокруг оси, перпендикулярной плоскости проекции, является частным случаем параллельного перемещения. Отличие от параллельного перемещения состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.

Способ вращения вокруг оси, перпендикулярной плоскости проекции, применим для перемещения отрезка прямой общего положения в частное.

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства параллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.

2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C'' и D'', следуя этому свойству, заняли положение C''₁ и D''₁.

3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

20. Многогранник - (определение) геометрическое тело, ограниченное со всех сторон плоскими многоугольниками – гранями. Стороны граней называются ребрами, а концы ребер - вершинами. По числу граней различают 4-гранники, 5-гранники и т.д. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани. Многогранник называется правильным, если его грани правильные многоугольники (т.е. такие, у которых все стороны и углы равны) и все многогранные углы при вершинах равны. Существует пять видов правильных многогранников:тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

21. 1.Поверхностьюназывается совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве по определённому закону. Следовательно, всякую поверхность можно представить как перемещение линии по другим линиям. Линия, образующая поверхность, называетсяобразующей. Линия, по которой перемещается образующая, называетсянаправляющей. Образующие могут быть постоянными и изменяться.

Образование поверхностей. Поверхность можно задать на чертеже, задав её множеством принадлежащих ей точек и линий. При этом точки выбирают так, чтобы они давали возможность с достаточной степенью точности определить форму поверхности и решать на ней различные задачи.

Поверхности на комплексном чертеже могут быть заданы:

1.Проекциями направляющих и способом перемещения по ним образующих.

2.Семейством линий, принадлежащих поверхности - каркасный способ задания поверхности.

3.Очерком поверхности, т.е. линиями, ограничивающими на комплексном чертеже область существования проекций.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой).

26. Разверткой поверхности называют плоскую фигуру, полученную в результате совмещения поверхности с плоскостью.

По развертыванию поверхности делятся на два класса:

развертываемые, которые можно совместить с плоскостью без разрывов и складок, и неразвертываемые, которые невозможно совместить с плоскостью без разрывов и складок.

Развертываются все многогранные поверхности, из кривых поверхностей – только линейчатые, у которых смежные образующие параллельны между собой (цилиндрические) или пересекаются по одной точке (конические). Все остальные поверхности относятся к неразвертываемым.

новные свойства развертки развертываемой поверхности:

1. Прямая на поверхности переходит на прямую на развертке.

Параллельные прямые на поверхности переходят в параллельные прямые при развертке.

3. Длина линии на поверхности равна ее длине на развертке.

Площадь развертки равна площади поверхности. Все размеры на развертке имеют натуральную величину.

Поделиться:

Воспользуйтесь поиском по сайту: