Комбинированные методы шифрования

Лабораторная работа № 11

 

Создание ПП для шифрования и дешифрования с помощью аналитических преобразований

Цель работы:

Изучить методы криптографического преобразования данных, ознакомиться с принципами шифрования.

Теоретические сведения:

 

Шифрование с помощью аналитических преобразований

Достаточно надежное закрытие информации может быть обес­печено при использовании для шифрования некоторых аналити­ческих преобразований. Для этого можно использовать методы ал­гебры матриц, например умножение матрицы на вектор по правилу:

Если матрицу А = (а₀) использовать в качестве ключа, а вместо компонента вектора B-(bj) подставить символы текста, то компо­ненты вектора С- (cj) будут представлять собой символы зашифро­ванного текста.

Приведем пример, взяв в качестве ключа квадратную матрицу третьего порядка

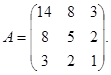
Заменим буквы алфавита цифрами, соответствующими их порядковому номеру в алфавите: А—0, Б—1, В—2 и т. д. Тогда отрывку текста ВАТАЛА будет соответствовать последовательность 2, 0, 19, 0, 12, 0. По принятому алгоритму шифрования выполним необходи­мые действия:

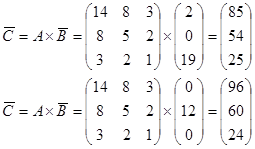
При этом зашифрованный текст будет иметь вид: 85, 54, 25, 96, 60, 24.

 

Дешифрование осуществляется с использованием того же пра­вила умножения матрицы на вектор, только в качестве ключа бе­рется матрица, обратная той, с помощью которой осуществляется зшифрование, а в качестве вектора-сомножителя — соответствую­щие фрагменты символов закрытого текста; тогда значениями век­тора-результата будут цифровые эквиваленты знаков открытого текста.

Матрицей, обратной данной А, называется матрица А^-1, получаю­щая из присоединенной матрицы делением всех ее элементов на определитель данной матрицы. В свою очередь присоединенной на­зывается матрица, составленная из алгебраических дополнений A_ij, к элементам данной матрицы, которые вычисляются по формуле:

где — определитель матрицы, получаемой вычеркиванием i-й строки и j-го столбца исходной матрицы А.

Определителем матрицы называется алгебраическая сумма п! членов (для определителя n-го порядка), составленная следующим образом: членами служат всевозможные произведения п элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член суммы берется со знаком «+», если его индексы состав­ляют четную подстановку, и со знаком «-» — в противоположном случае. Для матрицы третьего порядка, например, определитель вы­числяется следующим образом:

Тогда процесс раскрытия выглядит так:

Таким образом, получена последовательность знаков раскрыто­го текста 3, 0, 19, 0, 12, 0, что соответствует исходному тексту. Этот метод шифрования является формальным, что позволяет легко реа­лизовать его программными средствами.

Комбинированные методы шифрования

Одним из важнейших требований, предъявляемых к системе шифрования, является ее высокая стойкость. Однако повышение стойкости любого метода шифрования приводит, как правило, к су­щественному усложнению самого процесса шифрования и увеличе­нию затрат ресурсов (времени, аппаратных средств, уменьшению пропускной способности и т. п.).

Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т. е. последовательное шифрова­ние исходного текста с помощью двух или более методов.

Как показали исследования, стойкость комбинированного шиф­рования S_k не ниже произведения стойкостей используемых спосо­бов S_i т. е.

Комбинировать можно любые методы шифрова­ния и в любом количестве, однако на практике наибольшее распро­странение получили следующие комбинации: 1) подстановка + гаммирование; 2) перестановка + гаммирование; 3) гаммирование + + гаммирование; 4) подстановка + перестановка. Типичным приме­ром комбинированного шифра является национальный стандарт США криптографического закрытия данных (DES).

Кодирование

Одним из средств криптографического закрытия информации, также имеющим длительную историю практического использова­ния, является кодирование, под которым понимается замена элементов закрываемых данных некоторыми цифровыми, буквенными или комбинированными сочетаниями — кодами. Нетрудно заме­тить, что между кодированием информации и ее шифрованием под­становкой существует значительная аналогия. Однако между этими методами можно найти и различия.

При шифровании подстановкой заменяемыми единицами ин­формации являются символы алфавита, и, следовательно, шифрова­нию могут подвергаться любые данные, для фиксирования которых используется данный алфавит. При кодировании замене подверга­ются смысловые элементы информации, поэтому для каждого спе­циального сообщения в общем случае необходимо использовать свою систему кодирования. Правда, в последнее время разработаны специальные коды, имеющие целью сократить объем информации при записи ее в ЗУ.

Специфика этих кодов заключается в том, что для записи часто встречающихся символов используются короткие двоичные коды, а для записи редко встречающихся - длинные.

Примером такого кода для английского языка может служить код Хаффмена, показанный в таблице 3.2.

Такое кодирование имеет криптографическую стойкость на уровне шифрования простой заменой.

При смысловом кодировании основной кодируемой единицей является смысловой элемент текста. Для кодирования составляется специальная таблица кодов, содержащая перечень кодируемых эле­ментов и соответствующих им кодов. Введем, например, следую­щую кодовую таблицу:

Автоматизированные системы управления
Автоматизация управления
Осуществляет
Позволяет

Тогда предложение «Автоматизированные системы управления позволяют осуществлять автоматизацию управления» после кодиро­вания будет иметь вид: 001 632 415 002.

Выполнение работы:

Метод кодирования

Используя таблицу, зашифруете текст: In this book the reader will find a comprehensive survey.

Таблица 3.2	Коды Хаффмена
А
О
N
D
Р
V
К
Q
Z
X
J
R
I
Е
S
W
В
Н
F
С
М
U
G
Y

Метод Вижинера

Требуется зашифровать сообщение: МАКСИМАЛЬНО ДОПУСТИМОЙ ЦЕНОЙ ЯВЛЯЕТСЯ ПЯТЬСОТ РУБ ЗА ШТУКУ. В соответствии с пер­вым правилом записываем под буквами шифруемого текста буквы ключа.

Получаем: максимально допустимой ценой является пятьсот руб. за штуку - сальерисаль ерисальери салье рисальер исальер иса ль ериса

Дальше осуществляется непосредственное шифрование в соот­ветствии со вторым правилом, а именно: берем первую букву шифру­емого текста (М) и соответствующую ей букву ключа (С); по букве шифруемого текста (М) входим в рабочую матрицу шифрования и выбираем под ней букву, расположенную в строке, соответствующей букве ключа (С), — в нашем примере такой буквой является Э; вы­бранную таким образом букву помещаем в шифрованный текст. Эта процедура циклически повторяется до зашифрования всего текста.

Контрольный лист

 

Содержание отчета:

Вывод о проделанной работе_____________________________________________________

_____________________________________________________________________________

 

Контрольные вопросы:

1. Что из себя представляет блочная симметричная криптографическая система?__________________________________________________________________________________________________________________________________________________

 

2. Объясните, что такое композиционный блочный шифр и итерацион­ный блочный шифр:

__________________________________________________________________________________________________________________________________________________________

 

3. Какими характеристиками оценивается стойкость криптографических систем?___________________________________________________________________________________________________________________________________________________________________________

 

4. Что подразумевается под понятием «вычислительная сложность алго­ритма»?___________

__________________________________________________________________________________________________________________________________________________________

 

5. Для каких целей применяются случайные последовательности и про­стые числа в криптографии?________________________________________________________________

_____________________________________________________________________________

 

 

6. Чем характеризуются односторонние функции с секретом?___________________________

______________________________________________________________________________

 

7. Чем отличается криптографическая система с открытым ключом?_____________________

 

____________________________________________________________________________

Дата _______ Оценка_____________

Подпись преподавателя_________________

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: