Уравнения изопроцессов и постоянная адиабаты

ВВЕДЕНИЕ

Термодинамический процесс представляет собой переход газа из одного состояния в другое, характеризуемое иным, по сравнению с исходным, значением термодинамических параметров. Среди огромного многообразия процессов особое значение имеют так называемые изопроцессы, т.е. процессы, в которых один из параметров состояния остается неизменным. К таким процессам относятся: изобарический, изохорический, изотермический и адиабатический процессы.

Целью настоящей работы является изучение изохорного, изотермического и адиабатного процессов.

Уравнения изопроцессов и постоянная адиабаты

Состояния большинства реальных газов при давлениях от атмосферного и ниже удовлетворительно описываются уравнением состояния идеального газа (уравнение Менделеева-Клайперона):

(1.1)

где р — давление, V - объем, М - масса газа, - молярная масса, Т - температура, R - газовая постоянная. Рассмотрим изопроцессы идеального газа. В условиях постоянства температуры связь между давлением и объемом дается соотношением:

pV = const (1.2)

Или, разрешая (1.2) относительно р, получаем р = С/V, где С = (М/ 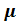)RТ - константа. Изучая в реальном эксперименте зависимость р от V в условиях, когда постоянство температуры обеспечено, можно не только убедиться в характере зависимости, но и, зная температуру, оценить количество вещества. Необходимым условием осуществления изотермического процесса является его медленное протекание, ибо только при этом условии возможно установление теплового равновесия между рабочим газом и окружающей средой, т.е., установление равенства температур между ними.

При изохорном процессе изменение состояния газа происходит при постоянном объеме (V = const => dV=0 => dA=pdV=0). В этом случае, при неизменном количестве газа, связь между давлением и температурой определяется уравнением:

(1.3)

Признаком адиабатического процесса является, как известно, отсутствие теплообмена с окружающей средой. Поэтому первое начало термодинамики dQ = dU + pdV может быть записано следующим образом:

0 = dU + pdV (1.4)

где dU – изменение внутренней энергии газа.

Используя величину C_V — молярную теплоемкость при постоянном объеме, уравнение (1.4) можно переписать

0 = v C_V dT + p dV (1.5)

где 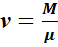— число молей вещества, Выражение (1.5) представляет собой дифференциальное уравнение, для решения которого необходимо выполнить известную процедуру разделения переменных. для этого выразим р из уравнения состояния, подставим в (1.5) и поделим уравнение на Т:

(1.6)

После деления (1.6) на C_V, приводим уравнение к виду

(1.7)

Интегрирование уравнения дает соотношение

(1.8)

С учетом известного уравнения Майера С_p = С_V + R, а также используя коэффициент Пуассона g = C_p / C_V, получаем уравнение адиабаты (уравнение Пуассона) в виде

TV ^g-1 = const (1.9)

Выражая Т из (1.1) и подставляя в (1.9), получаем уравнение Пуассона в переменных р, V

pV ^g = const (1.10)

Изучая зависимость между переменными р, V в адиабатическом процессе, можно определить коэффициент Пуассона γ (показатель адиабаты), который, как известно, связан с числом степеней свободы i молекулы газа соотношением

(1.11)

Знание i позволяет судить о конфигурации молекулы газа. Необходимым условием осуществления адиабатического процесса является его быстрое протекание, поскольку в этом случае теплообмен между газом и окружающей средой не успевает произойти, и таким образом выполняется условие теплоизоляции.

Уравнения (1.2) и (1.10) могут быть обобщены в виде уравнения

pV ⁿ = const (1.12)

где n принимает значения от 1 γ.

Процесс, описываемый уравнением (1.12) с любым постоянным показателем степени n называется политропным процессом, характеризуемым постоянством теплоемкости.

Рассмотрим метод определения γ используемый в данной работе (метод Клемана-Дезорма). Исследования адиабатического расширения газа, в данном методе удобно проводить в переменных P и T. Вначале в рабочий объем нагнетается воздух. Вследствие этого воздух нагревается. Далее происходит изохорическое остывание газа до температуры окружающей среды. После установления термодинамического равновесия с окружающей средой в рабочем объеме устанавливается состояние газа характеризуемое температурой Т ₁ равной температуре окружающей среды и давлением P ₁, которое превышает атмосферное давление P ₀ на небольшую величину P ′, т.е. P ₁ = P ₀ + P ′ и P ′ << P ₀. На короткое время откроем и закроем кран соединяющий рабочий объем с окружающей средой. После открытия крана давление упадет до атмосферного, а температура понизится ниже комнатной вследствие расширения газа. Это процесс можно считать адиабатным, если за время открытия крана теплообменом с окружающей средой можно пренебречь. В этом состоянии система будет характеризоваться давлением P ₂ = P ₀ и температурой T ₂ которая будет ниже комнатной T ₁ (температура понижается, поскольку расширение происходит за счет внутренней энергии газа). Преобразовав уравнение адиабаты (1.10) с помощью уравнения Менделеева-Клайперона (1.1) к переменным P и T получим:

(1.13)

После закрытия крана происходит медленное изохорическое нагревание системы через стенки сосуда до температуры окружающей среды T ₁. Вследствие нагрева давление в системе будет возрастать и установится какое-то давление P ₃ = P ₀ + P ″. Причем P ″ << P ₀. Изохорический процесс выравнивания температуры подчиняется закону Гей-Люссака:

(1.14)

Исключая с помощью (1.14) отношение температур T ₁/ T ₂ из (1.13), найдем

Отсюда, учитывая, что P ₂ = P ₀, находим γ

(1.15)

В нашем случае давления P ₁ и P ₃ отличаются от атмосферного на малые величины P ′ и P ″, соответственно. Разлагая логарифмы в ряд по малому параметру и пренебрегая членами второго и более высоких порядков малости в выражении 1.15, получим:

(1.16)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: