 |
Анализ цепи по постоянному току
|
|
|
|
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
АНАЛИЗ ЦЕПИ ПО ПОСТОЯННОМУ ТОКУ
Для получения схемы цепи постоянного тока необходимо приравнять значение частоты в выражениях е1(t), e2(t), e3(t) нулю.
Полученное значение для ЭДС источников определить их, как источники постоянной ЭДС – E1, E2, E3.
Привести эквивалентные схемы цепи постоянного тока в двух случаях - при подключении источников и при t→∞.
ОБЯЗАТЕЛЬНО ОБЪЯСНИТЬ ХАРАКТЕР И ПРИЧИНУ ИСПОЛЬЗОВАНИЯ ЭКВИВАЛЕНТНЫХ ЭЛЕМЕНТОВ.
Провести анализ схем(определить токи всех ветвей и напряжения на всех элементах), составив необходимое и достаточное число уравнений.
АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКОВ ВО ВРЕМЕННОЙ ОБЛАСТИ
Привести схему электрической цепи во временной области.
Составить необходимое и достаточное число уравнений цепи, применяя метод уравнений Кирхгофа.
Составить необходимое и достаточное число уравнений, применяя метод контурных токов.
Составить матрицы коэффициентов и правых частей уравнений.
Записать решение для токов в виде матричного соотношения.
УКАЗАНИЕ. Решение систем уравнений относительно неизвестных токов не проводить.
АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ
1.3.1. Перевести схему цепи из временной области в комплексную. Привести рисунок схемы в соответствующих обозначениях.
1.3.2. Перевести, полученные матричные уравнения в предыдущем пункте для метода уравнений Кирхгоффа и метода контурных токов, в комплексную форму
1.3.3. Составить необходимое и достаточное число уравнений по методу узловых потенциалов в комплексном виде.
1.3.4. Записать все три системы уравнений в матричной форме.
|
|
|
1.3.5. Решить две любые из систем. На основе полученного решения провести полный анализ схемы (определение токов всех ветвей и напряжений на всех элементах).
1.3.6. Перевести результаты анализа во временную форму.
1.3.7. Построить на комплексной плоскости векторную диаграмму напряжений путём обхода контура (по выбору студента) и убедиться в выполнении 2-го закона Кирхгоффа.
1.3.8. Определить сопротивления ветвей этого контура и построить их на комплексной плоскости в виде векторных диаграмм.
ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ВХОДНОГО СОПРОТИВЛЕНИЯ И ПЕРЕДАТОЧНОЙ ФУНКЦИИ
1.4.1. ПРЕОБРАЗОВАТЬ исходную схему электрической цепи
1.4.1.1 - исключить источники напряжения e1(t), e2(t), e3(t),
1.4.1.2 - преобразовать в схеме «звезду» в «треугольник».
1.4.2. Получить формулы для входного сопротивления со стороны узлов 1, 0, а также выражение для передаточной функции на узлах 3,0.
Получение этих выражений следует провести с помощью пакета MACHCAD. 1.4.3. Построить частотные характеристики по полученным выражениям входного сопротивления и передаточной функции в указанном пакете программ.
Первый диапазон частот брать от нуля до до 5000 р/с. Провести уточнение диапазона частот каждому студенту индивидуално с целью представления частотных характеристик наиболее информативно.
Графики АЧХ и ФЧХ делать в едином масштабе для совмещения и изучения хода кривых в локальных экстремумах.
Выделить в другом масштабе участки графиков, где наблюдаются локальные экстремумы кривых
Проверить частотные характеристики входного сопротивления и передаточной функции, используя программу схемотехнического моделирования MICRO-CAP.
Каждому значению частоты, для которого существует локальный экстремум, поставить в соответствие эквивалентную схему резонанса напряжений или резонанса токов.
Полученные частотные характеристики объяснить с помощью эквивалентных моделей схемы, которая была взята в пункте 1.4.1.1.
|
|
|
ПРИНЦИПИАЛЬНАЯ СХЕМА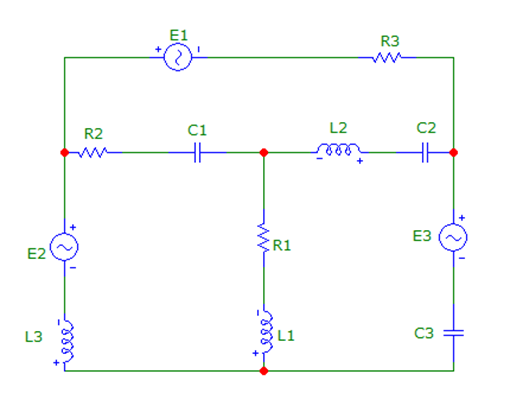 
R1=35 Ом; R2=50 Ом; R3=90 Ом;
L1=4,5 Гн; L2=19 Гн; L3=7,3 Гн;
C1=3,7 МкФ; C2=4 МкФ; C3=0,5 МкФ;
F=50 Гц;
E1(t)=1*sin(ωt-31); E2(t)=5*sin(ωt+17); E3(t)=10*sin(ωt-71)
Анализ цепи по постоянному току
ω1,ω2,ω3 приравниваем к нулю полученные значения ЭДС источников-источники постоянной ЭДС
E1(t)=1*sin(ωt-31); E1=sin(-31)≈-0,52В
E2(t)=5*sin(ωt+17); E2=sin(17)≈1,46В
E3(t)=10*sin(ωt-71);E3=sin(-71)≈-9,46В
1.1.1) При t 0(Рассматривается момент включения схемы)
 |
 |
| |||||||||||||||
 | |||||||||||||||
|
| ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 |
Iк1=0
Iк2=0 Применяем 2 закон Кирхгофа
Iк3=0
(к1) E1-UL1=0
(k2) E2-UL1-UL3=0
(k3) E3+UL1+UL2=0
 | |
E1=UL2 E1=UL2
E2-UL1-UL3=0 E2+E3+E1=UL2
E3+UL1+UL2=0 E3+E1=-UL1
UL1=-E3-E1=9,46+0,52=9,98 В
UL2=E1=-0,52 В
UL3=E1+E2+E3=-0,52+1,46-9,46=-8,52 В
Токи всех ветвей равны нулю: I = 0.
Напряжения на емкостных элементах равны нулю: Uc = 0.
1.1.2) При t ∞(Рассматривается стационарный процесс)
|
|
|
|
|
|
Iк1=0(из-за C2,C1)
Iк2=0(из-за C1) Применяем 2 закон Кирхгофа
Iк3=0(из-за C2,C3)
(к1) Е1-UC2-UC1=0
(к2) Е2+UC1=0
(к3) Е3-UC3+UC2=0
 | |||
| |||
E1-UC2+E2=0 E1+E2=UC2
E2=-UC1 E2=-UC1
E3-UC3+UC2=0 E3-UC1+E1+E2=0
UC1=-E2=-1,46 В
UC2=E1+E2=1,46-0,52=0,94 В
UC3=E1+E2+E3=-0.52+1,46-9,46=-8,52 В
Токи всех ветвей равны нулю: I = 0.
|
|
|
