Способы определения вероятнейшего места и исключения ошибок измерения.

ОМС по компасным пеленгам 3-х ориентиров.

Элементы теории способа. Сущность и порядок ОМС.

Способ ОМС по 3-м пеленгам основан на измерении 3-х пеленгов на ориентир. Каждому пеленгу соответствует своя изолиния – изоазимута. При визуальном измерении расстояния до ориентиров небольшие, значит на карте прокладываются непосредственно изолинии. Уравнение изолинии в общем виде:

Можно получить 3 уравнения, решая которые получим место судна. Можно получить тремя способами:

1. графический

2. графо – аналитический

3. аналитический

Прокладывая на карте 3 изолинии, из-за ошибок измерений они не пересекаются в одной точке и образуют треугольник. Если треугольник погрешностей мал, значит предполагается наличие в измерениях случайных погрешностей, если треугольник большой, значит наличие промаха или значительные систематические ошибки. Получив большой треугольник погрешностей следует выяснить причины появления треугольника. Для этого повторяют измерения, проявляя правильность опознавания и измерений. Установив причины приступают к определению вероятнейшего места судна и исключению ошибок измерений.

Виляние случайных ошибок:

При влиянии только случайных ошибок теоретические основы нахождения вероятнейшего места заключаются в следующем: Вероятнейшее место судна рассматриваем как точку пересечения изолиний соответствующих измеренным величинам функции U, исправленных поправками.

Выражая функции U через координаты точек и решая систему уравнений получим значение поправок. Определение производим с учётом весов отдельных ЛП.

Влияние систематических ошибок:

Следствие: ошибки при малой ΔМК. Для определения вероятнейшего места необходимо исключить эти ошибки.

Теоретические основы:

Составляются уравнения трёх изолиний: Решаются уравнения относительно неизвестных поправок. Решение приводит к выводу: необходимо провести биссектрисы углов под которыми пересекаются изолинии. Точки пересечения биссектрис – вероятнейшее место (геометрическое решение).

Сущность и порядок ОМС:

В быстрой последовательности берут пеленги, переводят их в ИП и прокладывают на карте в виде отрезков изолиний.

1. Заблаговременно подбираются надёжные ориентиры в соответствии с принципами подбора ориентиров

2. Производится опознавание ориентиров

3. Выполняется измерение пеленгов с учётом рекомендаций:

3.1. Первыми пеленгуются ориентиры, которые ближе к ДП

3.2. Если скорость <12 узлов, значит пеленги не приводят к одному моменту

3.3. Если скорость >12 узлов, то пеленги приводят к одному моменту (берётся 5 пеленгов A,B,C,B,A и рассчитываются средние значения A,B). фиксируется при пеленговании третьего ориентира.

3.4. При неодинаковой видимости ориентиров первыми берутся пеленги на измерение которых нужно затратить больше времени.

4. Определяются истинные пеленги.

5. ИП прокладываются на карте. Проложенные изолинии образуют треугольник. Появление треугольника погрешностей вызвано: промахами во взятии отсчётов, ошибки в опознавании, неправильно принятой ΔК и случайными ошибками в пеленговании.

6. Получив треугольник погрешностей выясняют причины.

7. Установив причины приступают к определению вероятнейшего места судна и исключению ошибок измерений.

Способы определения вероятнейшего места и исключения ошибок измерения.

При действии систематических ошибок:

1. По известным пеленгам ориентиров A, B, C рассчитываются углы между ИП получив два угла определяем место судна по двум углам, это и будет вероятнейшим местом. С карты снимают пеленги из этого места на ориентиры, это и будут ИП. Определяется ΔК по трём пеленгам:

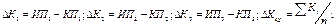
2. Учитываемую ΔК изменяют на 2-4° - разгон треугольника: прокладывают 6 изолиний (3 с учётом принимаемых поправок, 3 с учётом новой изменённой поправки), получаем два треугольника погрешностей. Через сходственные вершины треугольников проводят прямые линии, точка пересечения линий определяет действительное положение судна. Определяется и ΔК.

Покажем наиболее характерные расположения треугольников погрешностей:

Случай неопределённости

Если все ориентиры находятся на одной окружности или прямой, значит нельзя сделать ОМС - ситуация неопределённости. Случай неопределённости имеет место: если α+β+В=360° (все 3 ориентира и место судна на одной прямой), если α+β+В=180° (все 3 ориентира и место судна на одной окружности), где α, β- углы, В- угол при среднем ориентире:

 

При действии случайных ошибок:

Действие случайных ошибок отличается тем что ошибка каждого пеленга может иметь различное значение. В общем случае случайные ошибки так же вызовут появление треугольника. Исключить их действие невозможно, значит при действии только случайных ошибок определяется только вероятнейшее место.

Рассмотрим практические приёмы:

1. Если треугольник погрешностей мал, т. е. стороны его на путевой карте не превышают 3-5 мм и если треугольник близок к равностороннему, значит вероятнейшее место в его середине.

2. При равнобедренном и косоугольном треугольниках вероятнейшее место берётся ближе к меньшей его стороне и к углу близкому к прямому.

3. Метод смещения изолиний:

Для каждой изолинии рассчитывается смещение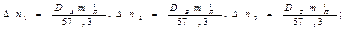

На карте прокладываются изолинии и от каждой прокладывается смещение:

Находят центр площади образованный перекрытиями всех трёх полос. Её центр- вероятнейшее место. Если все три полосы не перекрываются, значит нужно увеличить .

Совместное влияние:

При совместном действии необходимо выяснить: какая ошибка преобладает. Для этого при получении большого треугольника погрешностей повторяются наблюдения несколько раз (2-3 раза). Если в нескольких близких друг другу определениях размеры и ориентировка треугольников заметно не меняется, значит систематические ошибки преобладают. Если же размеры треугольников меняются, значит основное влияние оказывают случайные ошибки.

Практические методы:

1. Если углы между пеленгами ≈120° и получается равносторонний треугольник, значит вероятнейшее место в центре треугольника.

2. Повторяем наблюдения и получаем несколько треугольников близких друг к другу наблюдениях. Для каждого треугольника погрешностей определяем место одним из способов исключения методической ошибки и определяем ΔК (среднее арифметическое). Определяем оценку точности ΔК по методу наименьших квадратов Если ΔК_ср>m_Δ, значит преобладают систематические ошибки и ΔК_ср принимаем к учёту. Если ΔК_ср<m_Δ, значит ΔК_ср не принимаем.

Поделиться:

Воспользуйтесь поиском по сайту: