 |
Дополнительный член в формуле прямоугольников.
|
|
|
|
Содержание.
1. Введение. Постановка задачи……..…………………………2стр.
2. Вывод формулы……………………………………………….3стр.
3. Дополнительный член в формуле прямоугольников……….5стр.
4. Примеры………………………………………………………..7стр.
5. Заключение……………………………………………………..9стр.
6. Список литературы…………………………………………...10стр.
Постановка задачи.
Задача вычисления интегралов возникает во многих областях прикладной математики. В большинстве случаев встречаются определённые интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определёнными интегралами, сами подынтегральные функции не являются элементарными. Распространенными являются также случаи, когда подынтегральная функция задается графиком или таблицей экспериментально полученных значений. В таких ситуациях используют различные методы численногоинтегрирования, которые основаны на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью. Пусть требуется вычислить интеграл 
при условии, что a и b конечны и f(x) является непрерывной функцией на всем интервале (a, b). Значение интеграла I представляет собой площадь, ограниченную кривой f(x),осью x и прямыми x= a, x= b. Вычисление I проводится путем разбиения интервала от a до b на множество меньших интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок.
|
|
|
Вывод формулы прямоугольников.
Прежде, чем перейти к формуле прямоугольников, сделаем следующее замечание:
З а м е ч а н и е. Пусть функция f (x) непрерывна на сегменте [ a, b ], а
- некоторые точки сегмента [ a, b ]. Тогда на этом сегменте найдётся точка 
такая, что среднее арифметическое 
.
В самом деле, обозначим через m и M точные грани функции f (x) на сегменте [ a, b ]. Тогда для любого номера k справедливы неравенства 
. Просуммировав эти неравенства по всем номерам 
и поделив результат на n, получим
Так как непрерывная функция принимает любое промежуточное значение, заключённое между m и M, то на сегменте [a, b] найдётся точка такая, что
.
Первые формулы для приближенного вычисления определённых интегралов проще всего получаются из геометрических соображений. Истолковывая определенный интеграл 
как площадь некоторой фигуры, ограниченной кривой 
, мы и ставим перед собой задачу об определении этой площади.
Прежде всего, вторично используя эту мысль, которая привела к самому понятию об определенном интеграле, можно разбить всю фигуру (рис. 1) на полоски, скажем, одной и той же ширины 
, а затем каждую полоску приближенно заменить прямоугольником, за высоту которого принята какая-либо из ее ординат. Это приводит нас к формуле
(1)
где 
, а R – дополнительный член. Здесь искомая площадь криволинейной фигуры заменяется площадью некоторой состоящей из прямоугольников ступенчатой фигуры (или – если угодно – определенный интеграл заменяется интегральной суммой). Эта формула и называется формулой прямоугольников.
|
|
|
(рис.1)
На практике обычно берут 
; если соответствующую среднюю ординату 
обозначить через 
, то формула перепишется в виде
.
Дополнительный член в формуле прямоугольников.
Перейдём к отысканию дополнительного члена в формуле прямоугольников.
Справедливо следующее утверждение:
У т в е р ж д е н и е. Если функция f (x) имеет на сегменте [ a, b ] непрерывную вторую производную, то на этом сегменте найдётся такая точка
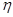, что дополнительный член R в формуле (1) равен
(2)
Доказательство.
Оценим 
, считая, что функция f(x) имеет на сегменте [- h, h ] непрерывную вторую производную Для этого подвергнем двукратному интегрированию по частям каждый из следующих двух интегралов:
Для первого из этих интегралов получим
Для второго из интегралов аналогично получим
Полусумма полученных для 
и 
выражений приводит к следующей формуле:
(3)
Оценим величину 
, применяя к интегралам и формулу среднего значения и учитывая неотрицательность функций 
и 
. Мы получим, что найдутся точка 
на сегменте [- h, 0] и точка 
на сегменте
[0, h ] такие, что
В силу доказанного замечания на сегменте [-h, h] найдётся точка 
такая, что 
Поэтому для полусуммы мы получим следующее выражение:
Подставляя это выражение в равенство (3), получим, что
(4)
где
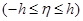. (5)
Так как величина 
представляет собой площадь некоторого прямоугольника с основанием 
(рис.1), то формулы (4) и (5) доказывают, что ошибка, совершаемая при замене 
указанной площадью, имеет порядок 
Таким образом, формула 
тем точнее, чем меньше h. Поэтому для вычисления интеграла 
естественно представить это интеграл в виде суммы достаточно большого числа n интегралов
И к каждому из указанных интегралов применить формулу (4). Учитывая при этом, что длина сегмента равна 
, мы получим формулу прямоугольников (1), в которой
Здесь 
. Мы воспользовались формулой, доказанной в утверждении, для функции 
|
|
|
