 |
Прямая линия на плоскости.
|
|
|
|
Скалярное произведение двух векторов.
. Следствия: а) 
,
б) 
.
Геометрическое свойство: 
.
Алгебраические свойства: 1.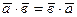 
;
2. 
;
3. 
;
4. 
; причем 
.
Выражение скалярного произведения в декартовых координатах:
Пусть 
, 
. Тогда 
.
Следствия: 1. 
2. 
3. Пусть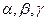 
- углы, которые вектор образует с осями координат ОХ, ОУ, ОZ.
Тогда 
, 
, 
, и
. (
называются направляющими
косинусами).
Векторное произведение двух векторов.
: 
;
- правая тройка;
.
Геометрические свойства: 1. 
.
2. 
есть площадь параллелограмма, построенного на
приведенных к общему началу векторах 
.
Алгебраические свойства: 1. 
;
2. 
;
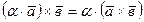3. 
;
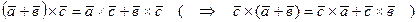4. 
для любого 
.
Выражение векторного произведения в декартовых координатах:
Пусть , . Тогда 
.
Следствие: 
.
3. Смешанное произведение трех векторов.
умножим векторно на 
; полученный вектор 
умножим скалярно на 
. Получившееся
число называется смешанным произведением векторов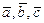 
.
Геометрический смысл: Смешанное произведение векторов 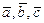равно объему параллелепипеда,
построенного на приведенных к общему началу векторах 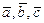, взятому со знаком “+”, если
тройка правая, со знаком “-“, если тройка левая. Если же векторы компланарны, их смешанное
произведение равно нулю.
Следствия: 1. 
2. 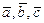компланарны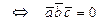 
3. если среди 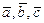два вектора коллинеарны, то 
.
Выражение смешанного произведения в декартовых координатах:
Пусть , , 
. Тогда 
.
Следствие: 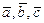компланарны 
.
.
.
Вопросы к коллоквиуму по векторной алгебре и аналитической геометрии.
(Учебник: В.А.Ильин, Э.Г.Поздняк “ Аналитическая геометрия “)
1. Скалярное произведение двух векторов (глава 2 параграф 2 пункты 2,3,4).
2. Векторное произведение двух векторов (глава 2 параграф 3 пункты 2,3,5,6).
|
|
|
3. Смешанное произведение трех векторов (глава 2 параграф 3 пункт 4).
4. Преобразование декартовых прямоугольных координат на плоскости (глава 3 параграф 1).
5. Различные виды уравнения прямой на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности прямых (глава 5 параграф 1 пункты 1,2,4,5,6).
6. Расстояние от точки до прямой на плоскости.
7. Плоскость в пространстве. Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей. Уравнение плоскости, проходящей через 3 точки (глава 5 параграф 3 пункты 1,3,4).
8. Расстояние от точки до плоскости.
9. Различные способы задания прямой линии в пространстве. Угол между прямыми. Условие параллельности и перпендикулярности прямых (глава 5 параграф 4 пункты 1,2,3,4).
10. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости (глава 5 параграф 4 пункт 6).
11. Эллипс: определение, каноническое уравнение (глава 6 параграф 1 пункт 1).
12. Парабола: определение, каноническое уравнение (глава 6 параграф 1 пункт 3).
13. Гипербола: определение, каноническое уравнение, асимптоты (глава 6 параграф 1 пункт 2,
параграф 2 пункт 2).
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Прямая линия на плоскости.
1. Преобразование декартовых прямоугольных координат на плоскости.
Пусть точка О’(a,b) – начало новой системы
координат O’X’Y’, оси которой повернуты на угол 
.
Тогда координаты точки в исходной и новой системах
координат связаны соотношениями
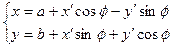
2. Общее уравнение прямой L: 
.
Cледствия: а) Пусть L: 
. Тогда вектор 
- нормальный вектор прямой
(т.е. 
).
б) Пусть L проходит через точку 
и перпендикулярна вектору .
Тогда L: 
.
3. Каноническое уравнение прямой.
Пусть L проходит через точку и параллельна вектору 
. (q называется
направляющим вектором прямой).
Тогда L: 
.
Следствие: Пусть L проходит через точки 
и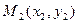 
.
|
|
|
Тогда L: 
.
4. Параметрические уравнения прямой.
Пусть L проходит через точку и параллельна вектору .
Тогда L: 
.
5.Прямая с угловым коэффициентом.
L: 
, где 
, b – смещение.
Следствие: Пусть L проходит через точку
и имеет угловой коэффициент k.
Тогда L: 
.
6. Угол между прямыми. Условие параллельности и перпендикулярности прямых.
Пусть 
; 
.
Тогда один из углов между прямыми совпадет с углом между их нормалями. Следовательно,
а) 
,
б) 
,
в) 
.
7. Расстояние от точки до прямой L: :
.
Следствие: Точки и 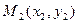лежат по одну сторону от прямой L (т.е. отрезок
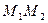не пересекает прямую L) в том и только в том случае, когда числа
и 
одного знака.
Плоскость в пространстве.
1. Общее уравнение плоскости 
.
Cледствия: а) Пусть . Тогда вектор 
- нормальный вектор
плоскости (т.е. 
).
б) Пусть 
проходит через точку 
и перпендикулярна вектору
. Тогда : 
.
2. Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей.
Пусть 
; 
.
Тогда один из углов между плоскостями совпадет с углом между их нормалями. Следовательно,
а) 
,
б) 
,
в)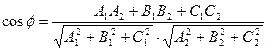 
.
3.Уравнение плоскости , проходящей через три различные точки 
, 
,
, не лежащие на одной прямой:
: 
.
4. Расстояние от точки до плоскости :
.
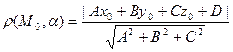Следствие: Точки и 
лежат по одну сторону от плоскости (т.е.
отрезок 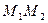не пересекает плоскость ) в том и только в том случае, когда числа
и 
одного знака.
|
|
|
