 |
Интегральная теорема Лапласа.
|
|
|
|
Бернулли,Муавр-Лаплас,Пуассон
1)Определение. Схемой Бернулли называется последовательность независимых в совокупности испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом успех в одном испытании происходит с вероятностью 
, а неудача — с вероятностью 
.
Под независимостью в совокупности испытаний понимается независимость в совокупности любых событий, относящихся к разным испытаниям. В испытаниях схемы Бернулли, когда с одним испытанием можно связать только два взаимоисключающих события, независимость в совокупности испытаний означает, что при любом 
независимы в совокупности события 
успех в первом испытании 
успех в -ом испытании 
. Эти события принадлежат одному и тому же пространству элементарных исходов, полученному декартовым произведением бесконечного числа двухэлементных множеств 
:
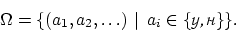
Здесь буквами «у» и «н» обозначены успешный и неудачный результаты испытаний соответственно.
Обозначим через 
число успехов, случившихся в испытаниях схемы Бернулли. Эта величина может принимать целые значения от нуля до в зависимости от результата испытаний. Например, если все испытаний завершились неудачей, то величина равна нулю.
Теорема (формула Бернулли). Для любого 
имеет место равенство:
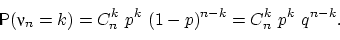
Доказательство. Событие 
означает, что в испытаниях схемы Бернулли произошло ровно 
успехов. Рассмотрим один из благоприятствующих событию 
элементарных исходов:
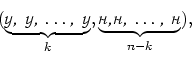
когда первые испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна 
. Другие благоприятствующие событию элементарные исходы отличаются лишь расположением успехов на местах. Есть ровно 
способов расположить успехов на местах. Поэтому событие состоит из элементарных исходов, вероятность каждого из которых также равна .
|
|
|
QED
Определение. Набор чисел 
называется биномиальным распределением вероятностей.
2) Пусть в каждом из 
независимых испытаний событие A может произойти с вероятностью 
, 
(условия схемы Бернулли). Обозначим как и раньше, через 
вероятность ровно 
появлений события А в испытаниях. кроме того, пусть 
– вероятность того, что число появлений события А находится между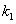 
и 
.
Локальная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
где 
- функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).
Интегральная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
P(n; k1, k2) 
где 
- функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
а) 
б) при больших 
верно 
.
Теоремы Лапласа дают удовлетворительное приближение при 
. Причем чем ближе значения 
к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).
3) При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 
вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
– среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для 
и 
. При больших 
рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
|
|
|
|
|
|
