Главная | Обратная связь | Поможем написать вашу работу!

Полная группа событий, противоположные события. Условная вероятность. Теорема умножения вероятностей.

Достоверное, невозможное, случайное события, совместные и несовместные события: 3 определения вероятностей.

* Достоверное событие - это событие, которое обязательно происходит при каждом проведении рассматриваемого эксперимента. Этому событию соответствует все множество исходов данного эксперимента;

* Невозможное событие – это событие, которое никогда не может произойти при проведении данного эксперимента. Этому событию соответствует пустое множество исходов данного эксперимента;

*Событие называется случайным если при одних и тех же условиях оно может как произойти, так и не произойти. Случайным считается событие, связанное со случайным экспериментом;

*Два события А и В называются совместным, если они могут произойти одновременно, при одном исходе эксперимента, и несовместными, если они не могут произойти одновременно ни при одном исходе эксперимента.

* 3 определения вероятностей

1.Классическое определение: Вероятностью P(A) события в данном опыте называется отношение числа m исходов опыта, благоприятствующих событию A, к общему числу n возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий: Р(А)=m/n

Свойства:

1. 0 ≤ P(A) ≤ 1

2.Вероятность достоверного события равна 1.

3. Вероятность невозможного события равна нулю.

4. P(A)= 1- P(A)

2. Частость события А называют статистической вероятностью, которая обозначается Р*(А)=mA/n, где mA - число экспериментов, в которых появилось событие А;

n - общее число экспериментов.

3. Аксиоматический подход к определению вероятности: третьим подходом к определению вероятности является аксиоматический подход, при котором вероятности задаются перечислением их свойств. В этом случае вероятность задается как числовая функция Р(А) на множестве всех событий, определяемых данным экспериментом, которая удовлетворяет следующим аксиомам:

1. 0≤P(A)≤1

2. P(A)=1, если А - достоверное событие.

3. P(A∩ B)=P(A)+P(B), если А и В несовместны.

4. Геометрическое определение вероятности: Пусть пространство элементарных событий 1 C представляет собой некоторую область плоскости. Тогда в качестве событий могут рассматриваться области А, содержащиеся в 1 C. Вероятность попадания в область А точки, наудачу выбранной из области 1 C, называется геометрической вероятностью события А и находится по формуле

P(A) = S(A)/S(C1) где S(A) и S(C1) – площади областей А и С1

Если С1 представляет собой отрезок P(A) = l(A)/L(C1) где l(A) и L(C1) – длины отрезков

Если С1 представляет собой трехмерную область P(A) = V(A)/V(C1) где V(A), V(C1) – объемы

Сумма, произведение событий. Формулы комбинаторики: перестановки, размещения, сочетания.

*Суммой событий А и В называется событие С=А+В, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А и В(т.е.или А, или В, или оба вместе).

*Произведением событий А и В называется событие С=А*В которое происходит тогда и только тогда, когда происходят оба события А и В.

*Разностью событий А и В называется событие С=А-В, которое происходит тогда и только тогда, когда происходит событие А, но не происходитсобытие В.

* Комбинаторика – раздел математики, в котором изучаются различные соединения (комбинации) элементов конечных множеств. Многие комбинаторные задачи могут быть решены с помощью двух правил –правила умножения и правила сложения.

* Размещением из n элементов по k элементов (0 £ k £ n) называется любое упорядоченное подмножество данного множества, содержащее k элементов.

А n = n(n-1)(n-2)…(n-k+1) = n!/(n-k)! Где n! = 1× 2 ×3×.....× n;

* Перестановкой из n элементов называется размещение из n элементов по n элементов.

Pn = An = n!

*Сочетанием из n элементов по k (0≤ k≤ n) называется любое подмножество данного множества, которое содержит k элементов. Любые два сочетания отличаются друг от друга хотя бы одним элементом.

C n = (n(n-1)(n-2)…(n-k+1))/k! = n!/(k!(n-k)!)

Теоремы сложения вероятностей для совместных и несовместных событий.

Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:

n n

P (∑ Ai) = ∑ P(Ai)

i=1 i=1

Сумма вероятностей событий, образующих полную группу, равна единице. События называются совместными, если они могут появиться одновременно в одном опыт.

Теорема. Вероятность сложения двух совместных событий равна суммевероятностей этих событий без вероятности их совместного появления: P(A+ B) = P(A)+ P(B)- P(AB)

Для трех событий А, В и С имеем: P(A+ B +C) = P(A)+ P(B)+ P(C)- P(AB)- P(AC)- P(BC)+ P(ABC)

Замечание. В случае трех и большего числа событий для нахождения вероятности суммы

S этих событий проще найти вероятность противоположного события S, а затем воспользоваться равенством P(S) =1- P(S).

Полная группа событий, противоположные события. Условная вероятность. Теорема умножения вероятностей.

*Условная вероятность

Пусть А и В – некоторые события, при чем P(B) > 0

Условной вероятностью события А при условии В называется вероятность события А, найденная при условии, что событие В произошло.

P (A) = (P(AB)) / P(B)

Аналогично определяется условная вероятность события В при условии А

P (B) = (P(AB)) / P(A) (P(A)≠0) или P(B/A) = (P(AB)) / P(A)

* Теорема (правило умножения вероятностей)

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

P(AB) = P(A) *P (B) = × или P(AB) = P(B) * P (A)

A B

Эта теорема обобщается на любое конечное число событий:

P (ABC… LM) = P(A) * P (B) * P (C) … P (M)

A AB AB..L

*Противоположные события

Событие А влечет событие В, если из того, что происходит событие А следует наступление события В А ∩ В

Противоположным событию А называется А, которое происходит тогда и только тогда, когда не происходит событие А.

*Полная группа событий

Полной группой событий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.

60. Стокса формула

Стокса формула, формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности S, ограниченной контуром L. С. ф. имеет вид:

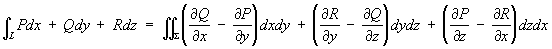причём направление обхода контура L должно быть согласовано с ориентацией поверхности S. В векторной форме С. ф. приобретает вид:

где а = Pi + Qj + Rk, dr — элемент контура L, ds — элемент поверхности S, n — единичный вектор внешней нормали к этой поверхности. Физический смысл С. ф. состоит в том, что циркуляциявекторного поля по контуру L равна потоку вихря поля через поверхность S. С. ф. предложена Дж. Г.Стоксом в 1854.

61. Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля пообъёму

, ограниченному этой поверхностью: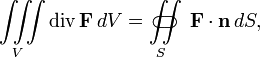

то есть интеграл от дивергенции векторного поля 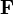, распространённый по некоторому объёму , равен потоку вектора через поверхность , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

63. Скалярные и векторные поля.

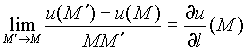- определение производной функции (скалярного поля) и(М) в точке М по направлению .

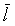- определение производной вектор-функции (векторного поля) в точке М по направлению l

Пусть функция задана в некоторой области пространства , . Поверхность в пространстве , определённая уравнением 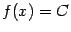, где 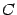-- постоянная, называется поверхностью уровня 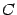функции . Если , то множество, заданное уравнением 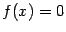, называется линией уровня.

64. Оператор (16.1)

называется оператором Гамильтона или набла-оператором и обозначается символом s

(«набла»).

Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю:

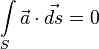Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.

Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля.

то есть для сил потенциалом 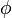является . Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия

дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Воспользуйтесь поиском по сайту: