 |
Приближённые формулы для определения объёмов древесины стволов и их частей
|
|
|
|
Содержание
Введение
Приближённые формулы для определения объёмов древесины стволов и их частей
Погрешность измерений
Таблицы объёмов древесных стволов
Определение запаса насаждений. Учёт запаса насаждений
Техника перечёта
Заключение
Список литературы
Приложение
Введение
Прибайкальский район, на территории которого расположены земли Прибайкальского сельского лесхоза, богат лесными ресурсами. Общая площадь земель в Прибайкальском лесхозе составляет 55591 га, из них 54082 га покрыты растительностью.
Ежегодно возникает необходимость производить всесторонний учёт запасов древесины.
Действия, направленные на учёт леса, определение объёмов древесины, называют лесной таксацией.
Лесная таксация имеет дело с измерениями, дающими объективную оценку леса, и при решении своих задач широко применяет способы математики. Различные математические расчёты и математический анализ, при многих графических построениях и изучении полученных кривых, используются методы аналитической геометрии. В своей работе я рассмотрела вопросы, связанные с вычислением объёмов деревьев.
При этом могут быть два случая: первый, когда требуется найти объёмов срубленного дерева, и второй, когда нужно найти объём растущего дерева.
Определить объём срубленного дерева проще, т.к. его можно непосредственно измерить на всём его протяжении. При нахождении объёма растущего дерева для установления его диаметров на различной высоте приходится применять иные приёмы, т.к. произвести замеры непосредственно на всём протяжении растущего дерева невозможно. В своей работе я провела математическое обоснование практических приёмов, применяемых при определении объёмов древесины на примере Прибайкальского сельского лесхоза.
|
|
|
Также я рассмотрела вопрос о погрешности измерений, возникающей при вычислении объёмов деревьев как срубленных, так и растущих.
Приближённые формулы для определения объёмов древесины стволов и их частей
Дерево состоит из корней, ствола и сучьев, образующие крону. Наиболее ценной частью дерева, на долю которой приходится в среднем 60–85% его объёма, является древесный ствол. Форма древесных стволов весьма разнообразна. У деревьев, выросших в густом лесу, ствол более правильной формы, у одиночно растущих деревьев – обычно неправильной, при этом у них сильно развита крона.
Если древесный ствол разрезать горизонтальной плоскостью, то в сечении будет круг или эллипс. Так, поперечные сечения ствола у сосны без коры во всех частях близки к эллипсам.
Площади кругов, по сравнению с эллипсами, дают незначительное превышение, вытекающее из следующего.
При равенстве a и b площади эллипса и круга равны. По мере увеличения разницы между величинами a и b увеличиваются также различия в площадях.
Если древесный ствол разрезать по сердцевине вертикальной плоскостью, то в сечении получится фигура, ограниченная кривой, которая расположена симметрично по отношению к вертикальной оси (Рис. 1).
При таком положении ствол можно рассматривать как тело вращения, ограниченное некоторой кривой. Зная уравнение этой кривой, можно было бы определить объём ствола. Многочисленные исследования кривых ствола показали, что они неправильны и непостоянны. Уравнения, точно определяющего характер этой кривой, до сих пор не найдено.
Образующая древесного ствола – слишком сложная кривая, и рассматривать мы её будем как сочетание разных кривых (рис. 3).
При обследовании большого количества стволов выясняется, что в нижней части ствола образующая имеет обычно вогнутую форму, на большей части ствола она выпуклая и лишь на коротких участках приближается к прямой.
|
|
|
Способы определения объёма ствола основываются на применении образующей ствола, характеризующейся уравнением
y2 = Ax2, (1)
У отдельных древесных пород в разных частях ствола показатель степени m изменяется от 0 до 3. В зависимости от значения m уравнения принимают следующий вид:
при m = 0 y2 = A (2)
при m = 1 y2 = Ax (3)
при m = 2 y2 = Ax2 (4)
при m = 3 y2 = Ax3 (5)
В первом случае формула (2) – это уравнение прямой, параллельной оси абсцисс. При вращении её вокруг оси абсцисс образуется цилиндр. Во втором случае (3) – это уравнение параболы второго порядка. Получаемое при этом тело вращения называется параболоидом второго порядка. В третьем случае (4) – две пересекающихся прямые при вращении образуют обыкновенный конус. И, наконец, в последнем случае (5) – это уравнение носит название уравнения параболы Нейля, а при вращении кривой такого рода получается нейлоид.
Отдельные части ствола приближаются к этим четырём геометрическим формам: нижняя – к нейлоиду, средняя (отдельные короткие отрезки) – к цилиндру, вершинная – к конусу, а большая часть – к параболоиду второго порядка.
Вычисление объёмов этих тел известны из курса стереометрии.
Vцил = Sосн * h
Vкон = 1/3 Sосн * h
Объём параболоида равен объёму цилиндра, имеющего с параболоидом одинаковые основания и высоту, умноженному на коэффициент f0=1/(2r+1). Этот множитель может быть близким к единице или меньше единицы, в зависимости от r. Множитель f0 называют коэффициентом абсолютной формы.
Тела вращения имеют следующие показатели:
Показатель Коэффициент
степени абсолютной
формы
Цилиндр………………………………………………0 1
Полукубический параболоид……………………….1/3 3/5
Параболоид Апполона……………………………….1/2 1/2
Кубический параболоид……………………………..2/3 3/7
Конус…………………………………………………..1 1/3
Нейлоид……………………………………………….3/2 1/4
Значения r вычисляются по формуле
,
где y2 и y1 – ординаты точек кривой; x2 и x1 – соответствующие абсциссы.
У древесных стволов чаще всего r варьирует от 8,51 до 0,55, что соответствует значению f0 от 0,49 до 0,45.
|
|
|
Великий русский учёный Д.И. Менделеев для определения объёмов стволов применил уравнение кубической параболы, характеризующее образующую древесного ствола:
g = A+Bx+Cx2+Dx3, (6)
где g – площадь сечения; x – расстояние от шейки корня до места измерения диаметров; A, B, C, D – некоторые постоянные коэффициенты.
По диаметрам в разных сечениях, определяемых по приведённым выше уравнениям, могут быть найдены площади поперечных сечений древесных стволов по следующей формуле (6). Определив площади поперечных сечений стволов, легко найти объём ствола или его части. Этот объём можно рассматривать как сумму бесконечно тонких поперечных отрезков, имеющих высоту dx и площадь основания g.
Соответственно этому
(7)
(8)
Первообразной для xn, будет функция 
, отсюда
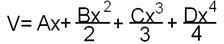(9)
Для определения объёма ствола или его части сначала можно ограничиться двумя членами подынтегрального выражения. В этом случае
g = A + Bx (10)
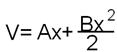(11)
Для нахождения коэффициентов А и В берут два конкретных сечения: g 0 – у основания ствола и g L – на расстоянии L от шейки корня и составляют два уравнения, определяющих площади этих сечений:
g0 = A + Bx0 и gL = A + BxL.
В этих уравнениях x 0 = 0, x L = L. Поэтому можем написать
g 0 = A; gL = A + BL.
Решая последнее уравнение относительно В, получим
Подставив в формулу (11) вместо A и B вычисленные значения этих коэффициентов и вместо x равную ему величину L, получим
Эта формула называется простой формулой Смалиана.
Возьмём одно поперечное сечение на половине целого ствола или его части, а второе – в тонком конце. Местоположение первого сечения определяется величиной L /2, а второго – на расстоянии L от основания ствола. Обозначив первое сечение через g L /2, а второе gL, можно написать
| |
Из первого уравнения вычтем второе
Заменив во втором уравнении величину A выражением 
, получим
Подставим найденные значения A и B в основную формулу (11)
|
|
|
Заменив x через L, получим
Обозначим поперечное сечение на половине ствола или его части gL/2 греческой буквой γ (гамма), тогда формула примет следующий вид:
V = γL.
Эта формула – основная в лесной таксацией. Она называется формулой срединного сечения или формулой объёмов цилиндров.
В рассмотренной формуле были использованы два члена подынтегрального выражения, для более точного результата можно взять три члена подынтегрального выражения. Проведя аналогичные вычисления, получим формулу
Эта формула пригодна для определения объёмов всех тел вращения: цилиндра, параболоида, конуса и нейлоида. И называется она формулой Ньютона. Располагая поперечные сечения в иных точках можно вывести другие формулы, а если ствол разделить на n отрезков длиной l, то получим формулу
Это сложная формула средних сечений. При пользовании рассмотренными выше простыми формулами для определения объёма древесный ствол уподобляют правильному геометрическому телу, в данном случае параболоиду, так как для образующей древесного ствола взято уравнение кубической параболы. Для определения объёма вершинной части применяют формулу объёма конуса V=1/3gh, где g – площадь основания, h – высота.
Из всех полученных формул наиболее удобна формула срединного сечения.
V = γL,
где γ – площадь срединного сечения, а L – расстояние от основания ствола. Эта формула имеет более высокую точность и применяется на практике.
Погрешность измерений
Форма круглого делового леса близка к усечённому конусу. Пусть R – радиус большего, r – радиус меньшего конца бревна. Тогда его почти точный объем (объём усечённого конуса) можно, как известно, найти по формуле
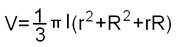
Пусть V1 – значение объёма, вычисленное по упрощённой формуле. Тогда 
;
ΔV = V – V1 = 
>0, т.е. V>V1. Значит, упрощённая формула даёт занижение величины объема. Так как ΔV/V= ¼ (r2+R2-2Rr)/(r2+R2+rR) < ¼, то допускаемая относительная погрешность не превзойдёт 25%. Положим теперь R/r = x. Тогда ΔV/V= ¼(1+x2-2x)/(1+x2+x) = ¼ f(x), 1<x<2.
Отсюда видно, что относительная погрешность не зависит от длины бревна, а определяется отношением R/r. Поскольку f ‘(x) = 3 (x2-1)/(1+x2+x)2>0 при x>1, то функция f возрастает на промежутке [1; 2]. Значит ΔV/V = ¼ f(x)<1/4 f(2)=1/28 при 1<x<2, и относительная погрешность не превосходит 3,6%.
В лесной практике такая погрешность считается вполне допустимой. С большей точностью практически невозможно измерить ни диаметр торцов (ведь они несколько отличаются от кругов), ни длину бревна, поскольку измеряют не высоту, а образующую конуса (длина бревна в десятки раз больше диаметра, и это не приводит к большим погрешностям). Таким образом, на первый взгляд неправильная, но более простая формула для объёма усечённого конуса в реальной ситуации оказывается вполне правомерной. Многократно проводившиеся с помощью специальных методов проверки показали, что при массовом учёте делового леса относительная погрешность при использовании рассматриваемой формулы не превосходит 4%.
|
|
|
|
|
|
12 |
