 |
Линейных пассивных четырехполюсников
|
|
|
|
Министерство образования и науки РФ
Пермский государственный технический университет
Кафедра конструирования РЭС
ПАССИВНЫЕ ЛИНЕЙНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
Варианты заданий и методические указания
К выполнению контрольной работы
По курсу «Основы теории цепей», часть II
Пермь 2005
УДК 681.3

Кузнецова Т.А., Кулютникова Е.А.
Пассивные линейные четырехполюсники: Варианты заданий и методические указания к выполнению контрольной работы по курсу «Основы теории цепей». Ч. II/ Перм. гос. техн. ун-т. – Пермь, 2005. – 23 с.
Изложены краткие теоретические сведения, задания и пример расчета пассивных линейных четырехполюсников. Предназначено для студентов всех отделений электротехнического, химико-технологического и аэрокосмического факультетов университета.
Рецензент канд. техн. наук Г.В. Кропачев
ãПермский государственный
технический университет, 2005
ЗАДАНИЕ
1. По номеру варианта вычертить схему, подлежащую расчету, и вычислить параметры элементов цепи.
2. Определить матрицу А -параметров. Проверить соответствие вычисленных А -параметров соотношению  . Вычислить значения сопротивлений элементов Т- и П-образной схем замещения и изобразить эти схемы.
. Вычислить значения сопротивлений элементов Т- и П-образной схем замещения и изобразить эти схемы.
3. Вычислить характеристические сопротивления, меру передачи, коэффициенты затухания и фазы.
4. Определить двумя способами передаточные коэффициенты kUU, kUI, kII, kIU для случая, когда четырехполюсник работает в согласованном режиме.
5. Вычислить двумя способами действующие значения входных и выходных токов и напряжений I 1, I 2, U 2 при нагрузке четырехполюсника на сопротивление  , если на вход четырехполюсника подать напряжение
, если на вход четырехполюсника подать напряжение  .
.
|
|
|
6. Найти значение передаточных коэффициентов kUU, kUI, kII, kIU при нагрузке четырехполюсника на сопротивление  .
.
7. Включить каскадно два заданных одинаковых четырехполюсника. Определить А -параметры эквивалентного четырехполюсника. Проверить соответствие рассчитанных А Э-параметров соотношению  . Определить двумя способами напряжение и ток, а также активную, реактивную, полную и мгновенную мощности (P, Q, S, p (t)) на входе и выходе полученной цепи, если ток на входе
. Определить двумя способами напряжение и ток, а также активную, реактивную, полную и мгновенную мощности (P, Q, S, p (t)) на входе и выходе полученной цепи, если ток на входе 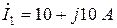 при согласованной нагрузке и при
при согласованной нагрузке и при  . Проверить выполнение баланса мощности.
. Проверить выполнение баланса мощности.
Выбор варианта
1. Расчетная цепь выбирается из схем, приведенных на рис. 1 – 35. Для первых 35 вариантов принимается режим прямого питания четырехполюсника (вход – зажимы 1–1¢, выход – зажимы 2–2¢), в следующих 35 вариантах – режим обратного питания (вход – зажимы 2–2¢, выход – зажимы 1–1¢), остальные 30 вариантов как первые.
2. Выбор варианта производится по последним двум цифрам зачетной книжки или задается преподавателем по его усмотрению.
3. Значения параметров цепи находятся из соотношения
 ,
,
где K – индекс сопротивления в схеме,
M выбирается в соответствии с табл. 1.
 |


Таблица 1
| Значение M для специальностей | |||||||||||
| нормативные сроки обучения | сокращенные сроки обучения (ускоренники) | ||||||||||
| АТ ТК | АСУ АУЦ | АЭП КЗИ | АТП | ЭС | КТЭИ | АТ | ТК | АСУ | АЭП | ЭС | КТЭИ АТП |
| 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАСЧЕТУ
ЛИНЕЙНЫХ ПАССИВНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
При расчете значений элементов А -матрицы можно воспользоваться параметрами холостого хода и короткого замыкания  ,
,  ,
,  ,
, 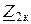 .
.
 ,
,  равны выходным сопротивлениям четырехполюсника со стороны входа при соответственно разомкнутых и замкнутых накоротко вторичных (выходных) зажимах четырехполюсника, а
равны выходным сопротивлениям четырехполюсника со стороны входа при соответственно разомкнутых и замкнутых накоротко вторичных (выходных) зажимах четырехполюсника, а  ,
, 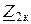 – входным сопротивлениям четырехполюсника со стороны вторичных зажимов при соответственно разомкнутых и замкнутых накоротко первичных (входных) зажимах четырехполюсника.
– входным сопротивлениям четырехполюсника со стороны вторичных зажимов при соответственно разомкнутых и замкнутых накоротко первичных (входных) зажимах четырехполюсника.
|
|
|
Зная значения любых трех параметров  ,
,  ,
,  ,
, 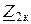 , можно определить А -параметры по следующим формулам:
, можно определить А -параметры по следующим формулам:
 ,
,  . (1)
. (1)
Из двух значений, определяемых при извлечении корня, правильно выбирается одно. Правильность расчета А -параметров можно проверить, используя соотношение
 . (2)
. (2)
Поскольку любой пассивный линейный четырехполюсник характеризуется тремя независимыми параметрами, его можно представить в виде эквивалентных Т- и П-образных схем замещения (рис. 36).
При этом значения элементов Т-образной схемы находятся из соотношений:
 . (3)
. (3)
Параметры П-образной схемы могут быть определены следующим образом:
 . (4)
. (4)
 |
Связь между токами и напряжениями на входе и выходе четырехполюсника можно выразить с помощью характеристических сопротивлений
 и
и  и меры передачи
и меры передачи
 ,(5)
,(5)
где  – коэффициент ослабления (затухания),
– коэффициент ослабления (затухания),  – коэффициент фазы.
– коэффициент фазы.
Значения характеристических сопротивлений находятся из выражений:

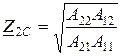 (6)
(6)
или

 . (7)
. (7)
Мера передачи однозначно определяется из формулы
 (8)
(8)
или
 . (9)
. (9)
Коэффициенты передачи  ,
,  ,
,  ,
,  характеризуют связь между значениями напряжения и токов на входе с напряжением и током на выходе:
характеризуют связь между значениями напряжения и токов на входе с напряжением и током на выходе:
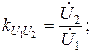


 (10)
(10)
При согласованной нагрузке, т.е. при подключении к выходным зажимам четырехполюсника  , имеют место следующие выражения:
, имеют место следующие выражения:
 (11)
(11)
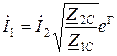 . (12)
. (12)
Отсюда
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
Зная сопротивление нагрузки  , можно найти значение входного сопротивления со стороны первичных зажимов
, можно найти значение входного сопротивления со стороны первичных зажимов
 . (17)
. (17)
Для определения коэффициентов передачи  ,
,  ,
,  ,
,  при произвольной нагрузке воспользуемся соотношениями
при произвольной нагрузке воспользуемся соотношениями
 (18)
(18)
Из этих выражений можно найти
 (19)
(19)
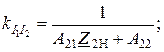 (20)
(20)
 (21)
(21)
 (22)
(22)
Цепная схема включения четырехполюсников (каскадное соединение) изображена на рис. 37.
 |
При этом
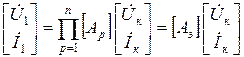 . (23)
. (23)
Для двух четырехполюсников, соединенных по каскадной схеме,
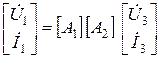 . (24)
. (24)
Эквивалентная матрица для двух четырехполюсников, соединенных каскадно,
 . (25)
. (25)
Пример расчета
Схема, подлежащая расчету, представлена на рис. 38. Параметры элементов цепи:


1. Определение A -параметров.
Найдем параметры холостого хода и короткого замыкания
 ;
;



A -параметры определяем по формулам (1)
 ,
, 


Правильность расчетов проверяем по соотношению (2)
|
|
|
 Точность расчета
Точность расчета
 .
.
Таким образом, получили следующую матрицу А -параметров:

2. Определение параметров эквивалентной Т-образной схемы замещения по формулам (3):
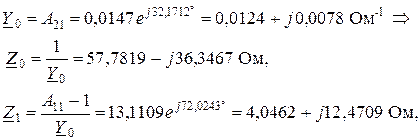

 |
Полученная Т-образная схема замещения представлена на рис. 39 (сопротивления указаны в Омах).
3. Определение параметров эквивалентной П-образной схемы замещения по формулам (4):

 |
Полученная П-образная схема замещения представлена на рис. 40 (сопротивления указаны в Омах).
4. Определение характеристических параметров четырехполюсника  ,
,  ,
,  .
.
Способ 1. Использование А -параметров четырехполюсника. По формулам (6) получим



Из формулы (8):


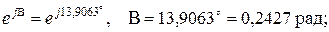

Способ 2. Использование параметров холостого хода и короткого замыкания. По формулам (7) найдем:

 а по формуле (9)
а по формуле (9)

или

Отсюда для определения меры передачи  поступим следующим образом:
поступим следующим образом:

откуда



5. Определение передаточных коэффициентов при условии, что четырехполюсник работает в согласованном режиме, т.е. в качестве нагрузки используется характеристическое сопротивление  .
.
Способ 1. Использование А -параметров четырехполюсника. По формулам (19) – (22) получим:




Аналогично рассчитываются передаточные функции для  .
.
Способ 2. Передаточные параметры также можно определить через вторичные (характеристические) параметры по формулам (13) – (16):
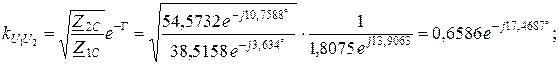



6. Вычисление действующих значений входных и выходных токов и напряжений I 1, I 2, U 2 при нагрузке четырехполюсника на сопротивление  при условии, что на вход четырехполюсника подано напряжение
при условии, что на вход четырехполюсника подано напряжение  .
.
Перейдем от мгновенного значения входного напряжения к соответствующему комплексному действующему значению

Тогда вычислить действующие значения входных и выходных токов и напряжений I 1, I 2, U 2 можно следующими способами.
Способ 1. При помощи характеристических параметров, используя формулы (11) – (12),
– определение выходного напряжения

мгновенное значение выходного напряжения

Действующее значение  можно было также вычислить по формуле:
можно было также вычислить по формуле:

– Определение входного тока
|
|
|

мгновенное значение входного тока
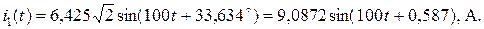
Действующее значение 
– Определение выходного тока
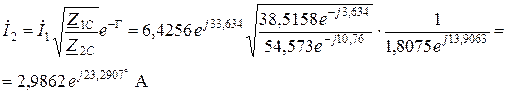
или по формуле

Мгновенное значение выходного тока

Действующее значение 
Способ 2. При помощи передаточных коэффициентов, используя формулы (19) – (22):
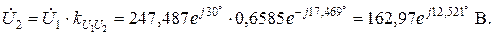


|
|
|


