 |
Математико-статистические таблицы
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ГОРОДСКОГО ХОЗЯЙСТВА ИМЕНИ О.Н. БЕКЕТОВА
ЖУРАВЕЛЬ В.В., ВОРОНКОВ А.А.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОГО ЗАДАНИЯ
ПО КУРСУ: ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ
МОДЕЛИ И МЕТОДЫ
Эконометрика
ХАРЬКОВ 2012
ОБЩИЕ ПОЛОЖЕНИЯ
Современный экономист должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели. Быстрое развитие и широкое применение средств вычислительной техники предопределяют требования к подготовке современного экономиста, который должен с помощью современных пакетов прикладных программ уметь анализировать сложные социально-экономические явления. Экономико-математическое моделирование - один из базовых курсов подготовки экономистов. Эта дисциплина основана на фундаменте знаний экономической теории, матричной алгебры, теории математической и общей статистики.
Для закрепления знаний по данному курсу и приобретения навыков, необходимых для построения и анализа экономико-математических моделей, для студентов заочного отделения предусмотрена контрольная работа. Контрольная работа включает перечень задач по основным темам курса, которые студенты выполняют самостоятельно. Контрольная работа должна быть оформлена в соответствии с установленными требованиями, обязательно должна соответствовать номеру варианта, содержать условия решаемых задач, необходимые расчеты и пояснения, выводы. Номер варианта определяется по последним цифрам номера зачетной книжки. После сдачи на проверку контрольная работа проверяется и при условии правильного решения допускается к защите студентом на экзамене. Если контрольная работа не зачтена, ее необходимо переработать в соответствии с представленными замечаниями.
|
|
|
Ввиду большого объема вычислений при построении и анализе экономико-математических моделей, в контрольных работах разрешается использовать современные пакеты прикладных статистических программ: STATISTICA, SPSS, SAS, Econometric Views, Mesosaur- Econometric, Excel и т. д.
При выполнении контрольной работы особое внимание следует обратить на базовые понятия, основные формулы расчетов характеристик экономико-математических моделей, примеры их построения и анализа, которые приведены ниже.
Пример. Парная регрессия и корреляция
По предприятиям, производящим однородную продукцию приводятся данные за 200X г.
| Номер предприятия | Объем производства продукции, ед. продукции, 
| Затраты, грн., 
|
Требуется:
1. Построить линейное уравнение парной регрессии от .
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции с помощью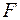 
-критерия Фишера и 
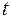-критерия Стьюдента.
4. Выполнить прогноз затрат при прогнозном значении объема производства продукции , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике построить исходные данные и теоретическую прямую.
Решение
1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу.
| Номер предприятия |
|
| 
| 
| 
| 
| 
| 
|
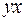
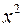
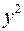
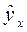
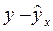
| -16 | 12,0 | |||||||
| -4 | 2,7 | |||||||
| -23 | 17,2 | |||||||
| 2,6 | ||||||||
| 1,9 | ||||||||
| 10,8 | ||||||||
| 0,0 | ||||||||
| 0,0 | ||||||||
| 5,3 | ||||||||
| 3,1 | ||||||||
| 7,5 | ||||||||
| -10 | 5,8 | |||||||
| Итого | 68,9 | |||||||
| Среднее значение | 85,6 | 155,8 | 13484,0 | 7492,3 | 24531,4 | – | – | 5,7 |
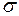
| 12,84 | 16,05 | – | – | – | – | – | – |
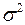
| 164,94 | 257,76 | – | – | – | – | – | – |
;
|
|
|
.
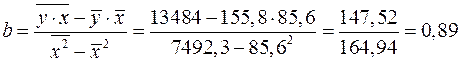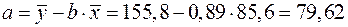Получено уравнение регрессии: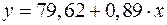 
.
С увеличением объема производства на 1 ед. затраты возрастают в среднем на 0,89 грн.
2. Тесноту линейной связи оценит коэффициент корреляции:
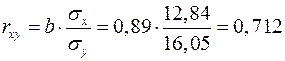; R2= 
.
Это означает, что 51% вариации затрат () объясняется вариацией фактора – объема производства.
Качество модели определяет средняя ошибка аппроксимации:
.
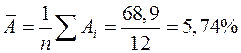Качество построенной модели оценивается как хорошее, так как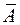 
не превышает 8-10%.
3. Оценку значимости уравнения регрессии в целом проведем с помощью 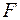-критерия Фишера. Фактическое значение 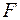-критерия:
.
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 
и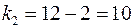 
составляет 
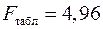. Так как 
, то уравнение регрессии признается статистически значимым.
Оценку статистической значимости параметров регрессии проведем с помощью 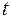-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.
Табличное значение 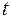-критерия для числа степеней свободы 
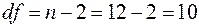и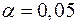 
составит 
.
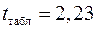Определим случайные ошибки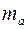 
, 
, 
:
;
;
.
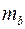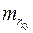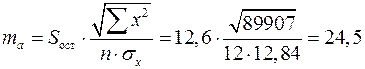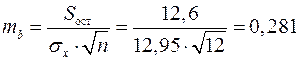Тогда
;
;
.
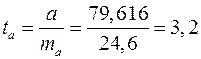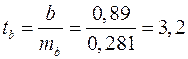Фактические значения 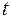-статистики превосходят табличное значение:
; 
; 
,
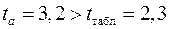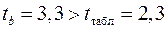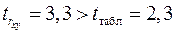поэтому параметры 
, 
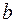и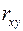 
не случайно отличаются от нуля, а статистически значимы.
Рассчитаем доверительные интервалы для параметров регрессии и 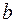. Для этого определим предельную ошибку для каждого показателя:
;
.
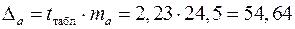Доверительные интервалы
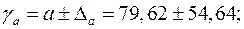
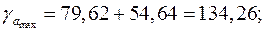
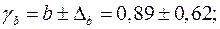
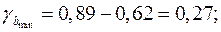
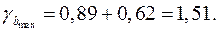
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью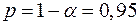 
параметры и 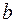, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение объема производства составит: 
ед. продукции, тогда прогнозное значение затрат составит: 
грн.
|
|
|
5. Ошибка прогноза составит:
Предельная ошибка прогноза, которая в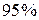 
случаев не будет превышена, и составит:
грн.
Доверительный интервал прогноза:
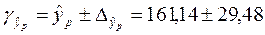грн.;
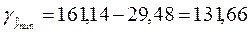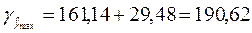грн.;
грн.;
Выполненный прогноз затрат является надежным (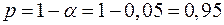
) и находится в пределах от 131,66 грн. до 190,62 грн.
6. В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. 1):
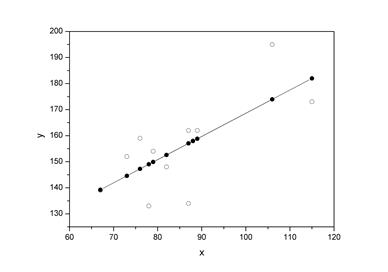
Рис. 1.
Варианты индивидуальных заданий
По предприятиям, производящим однородную продукцию приводятся данные за 20XX г. (см. таблицу своего варианта).
Требуется:
1. Построить линейное уравнение парной регрессии от .
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции с помощью 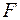-критерия Фишера и 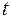-критерия Стьюдента.
4. Выполнить прогноз затрат при прогнозном значении объема производства , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике построить исходные данные и теоретическую прямую.
Вариант 1
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 2
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 3
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
|
|
|
Вариант 4
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 5
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 6
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 7
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 8
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 9
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Вариант 10
| Номер предприятия | Объем производства продукции, ед. продукции,
| Затраты, грн.,
|
Математико-статистические таблицы
Таблица значений 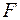-критерия Фишера при уровне значимости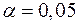 
| 
| |||||||||
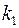
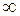
| 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 233,9 | 238,9 | 243,9 | 249,0 | 254,3 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
|
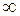
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
|
|
|
Критические значения 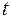-критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01 (двухсторонний)
| Число степеней свободы d.f. |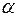 
| Число степеней свободы d.f. |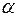
| ||||
| 00,10 | 0,05 | 0,01 | 00,10 | 0,05 | 0,01 | ||
| 6,3138 | 12,706 | 63,657 | 1,7341 | 2,1009 | 2,8784 | ||
| 2,9200 | 4,3027 | 9,9248 | 1,7291 | 2,0930 | 2,8609 | ||
| 2,3534 | 3,1825 | 5,8409 | 1,7247 | 2,0860 | 2,8453 | ||
| 2,1318 | 2,7764 | 4,5041 | 1,7207 | 2,0796 | 2,8314 | ||
| 2,0150 | 2,5706 | 4,0321 | 1,7171 | 2,0739 | 2,8188 | ||
| 1,9432 | 2,4469 | 3,7074 | 1,7139 | 2,0687 | 2,8073 | ||
| 1,8946 | 2,3646 | 3,4995 | 1,7109 | 2,0639 | 2,7969 | ||
| 1,8595 | 2,3060 | 3,3554 | 1,7081 | 2,0595 | 2,7874 | ||
| 1,8331 | 2,2622 | 3,2498 | 1,7056 | 2,0555 | 2,7787 | ||
| 1,8125 | 2,2281 | 3,1693 | 1,7033 | 2,0518 | 2,7707 | ||
| 1,7959 | 2,2010 | 3,1058 | 1,7011 | 2,0484 | 2,7633 | ||
| 1,7823 | 2,1788 | 3,0545 | 1,6991 | 2,0452 | 2,7564 | ||
| 1,7709 | 2,1604 | 3,0123 | 1,6973 | 2,0423 | 2,7500 | ||
| 1,7613 | 2,1448 | 2,9768 | 1,6839 | 2,0211 | 2,7045 | ||
| 1,7530 | 2,1315 | 2,9467 | 1,6707 | 2,0003 | 2,6603 | ||
| 1,7459 | 2,1199 | 2,9208 | 1,6577 | 1,9799 | 2,6174 | ||
| 1,7396 | 2,1098 | 2,8982 |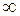
| 1,6449 | 1,9600 | 2,5758 |
Литература
Основная:
1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.
2. Практикум по эконометрике: Учебн. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.
3. Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. – Казань: ТИСБИ, 2002. – 56 с.
4. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – 402 с.
5. Замков О.О. Математические методы в экономике.- М., 2001.
6. Федосеев. Экономико-математические методы и прикладные модели.- Юнити, 2001.
Дополнительная:
7. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.
8. Зайцев Г.Ф. Исследование операций, 1976.
9. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – М.: Дело, 2001. – 400 с.
10. Катышев П.К., Магнус Я.Р., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 2002. – 208 с.
11. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2-х т. – Т. 1. Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика. – М: ЮНИТИ-ДАНА, 2001. – 656 с.
12. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2-х т. – Т. 2. Айвазян С.А. Основы эконометрики. – М: ЮНИТИ-ДАНА, 2001. – 432 с.
13. Эконометрика: Учебник / Тихомиров Н.П., Дорохина Е.Ю. – М.: Издательство «Экзамен», 2003. – 512 с.
14. Сборник задач по эконометрике: Учебное пособие для студентов экономических вузов / Сост. Е.Ю. Дорохина, Л.Ф. Преснякова, Н.П. Тихомиров. – М.: Издательство «Экзамен», 2003. – 224 с.
15. Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. – 304 с.
16. Эконометрика: Учебн. пособие для вузов / А.И. Орлов – М.: Издательство «Экзамен», 2002. – 576 с.
17. Мардас А.Н. Эконометрика. – СПб: Питер, 2001. – 144 с.
18. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебн. пособие для вузов. – М.: Высш. шк., 2002. – 479 с.
|
|
|
