 |
Перечислить основные свойства параллельного проецирования (продемонстрировать их на примерах).
|
|
|
|
Сущность метода аксонометрических проекций (привести примеры его практической реализации).
Аксонометрическая проекция — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
9 ) Что собой представляет прямоугольная параллельная проекция, где и в каких случаях она находит применение?
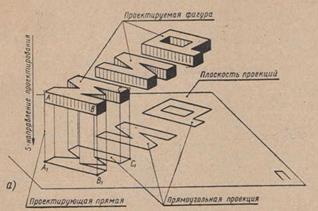 Представим себе в пространстве плоскость проекций П и слово «мир».
Представим себе в пространстве плоскость проекций П и слово «мир».
Выберем направление проектирования S, которое не должно быть параллельным плоскости проекций П.
Чтобы спроектировать слово «мир» на плоскость П по выбранному направлению проектирования S, надо через вершины.углов букв провести проектирующие прямые параллельно выбранному направлению до пересечения с плоскостью проекций П.
Полученные точки пересечения соединить соответствующим образом, тогда получают изображение слова «мир», называемое параллельной проекцией данного слова.
Параллельные проекции делятся на прямоугольные и косоугольные.
Прямоугольные (или ортогональные) - проектирующие лучи перпендикулярны плоскости проекций.
|
|
|
10) Прямоугольная проекция точки, прямой, плоскости.
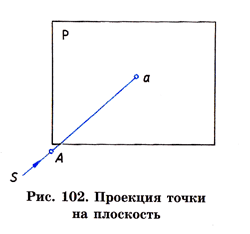
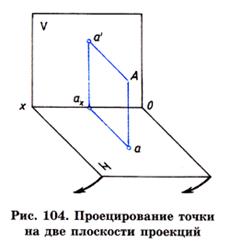
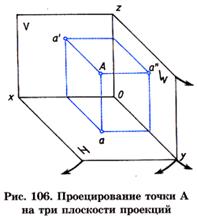
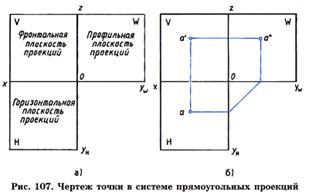
1. Проекция точки на данную плоскость проекций есть точка.
2. Любая проецируемая точка имеет одну проекцию на выбранной плоскости проекций.
3. Проекция точки, лежащей на плоскости проекций, совпадает с самой точкой
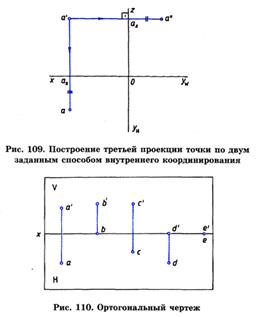
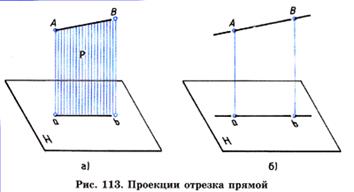
Вывод:
1. Проекция отрезка прямой, полученная при прямоугольном проецировании на плоскость проекций, не может быть больше самого отрезка.
2. Если отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину.
3. Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку.
4. Если в пространстве отрезок прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного).
5.Плоскость проецируется как совокупность 3х точек не лежащих на 1 прямой, и т.п.
Что называется коэффициентом искажения проецируемого объекта? Какие условия проецирования определяют величину коэффициентом искажения?
Величина угла, между плоскостями, на которые осуществляется проекция, определяет коэффициент искажения. Коэффициент искажения есть отношение длины проекции отрезка к его истинной длине.
18. Что называется показателем искажения в аксонометрии?Отношение единицы измерения по аксонометрическим осям (аксонометрическая единица) к единице измерения по осям x, y, z (натуральная единица) называется показателем искажения в аксонометрии.
коэффициент искажения может принимать любые числовые значения в зависимости от наклона отрезка и проецирующих лучей к плоскости проекций. В частности, если направление отрезка совпадает с направлением проецирования, то проекцией этого отрезка будет точка, а коэффициент искажения равен нулю.
|
|
|
Перечислить основные свойства параллельного проецирования (продемонстрировать их на примерах).
Основные свойства параллельного проецирования
1. Свойство однозначности. Проекцией точки на плоскость есть точка.
2. Свойство прямолинейности. Проекцией прямой линии на плоскость есть прямая.
3. Свойство принадлежности. Если точка принадлежит линии, то проекция точки принадлежит проекции этой линии.
4. Свойство сохранения параллельности. Проекциями параллельных прямых являются параллельные прямые.
5. Свойство деления отрезка в отношении. Если отрезок прямой линии делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении.
6. Свойство параллельного переноса. Проекция фигуры не меняется при параллельном переносе плоскости проекций. Три последние свойства обеспечивают более простое построение изображения и меньше искажают форму и размеры оригинала по сравнению с центральной проекцией.
|
|
|


