 |
Разработка программ для работы с элементами множества
|
|
|
|
В Прологе, в отличие от некоторых императивных языков программирования, нет такой встроенной структуры данных, как мно-жество. Поэтому под множеством будем понимать список, который не содержит повторных вхождений элементов. Разработаем предикаты, которые реализуют основные теоретико-множественные операции.
Пример 5.1. Создать предикат, превращающий произвольный список в множество. Для того, чтобы исходный список можно было считать множеством, нужно удалить все повторные вхождения элементов. Для решения этой задачи можно воспользоваться предикатами member (см. стр. 25) и delete (см. стр. 29), изменив при этом тип данных в разделе domains на числовой. Назовем этот предикат list_set.
domains
i = integer
listI = i*
predicates
list_set(listI, listI)
member(integer, listI)
clauses
member(X,[X|_]).
member(X,[_|T]):- member(X,T).
list_set([],[]).
list_set([X|S1],S2):-
member(X,S1),!, list_set(S1, S2).
list_set([X|S1],[X|S2]):- list_set(S1,S2).
Например, если задать цель
goal
list_set([2,3,4,1,2,5,2,3,5,1,2,2,4],L).
то результатом будет список L=[3,5,1,2,4].
Факт принадлежности элемента x множеству A обозначается 
.
Пример 5.2. Построить предикат, проверяющий, принадлежит ли элемент данному множеству.
Для решения этой задачи можно использовать модификацию предиката member, добавив в факт отсечение, которое позволит не производить поиск, если искомый элемент первый в списке.
member_new(X,[X|_]):–!.
member_new(X,[_|T]):– member_new(X,T).
Пример 5.3. Создать предикат, находящий мощность мно-жества. Мощностью множества A называется число его элементов, обозначается 
. Так, для множества 
мощность 
.
length([], 0). % в пустом списке элементов нет
length([_|T], L):–
length(T, L_S), % L_S – число элементов в хвосте
L = L_S + 1. % L – число эл-в исходного списка
При определении предиката length неважно, чему равен первый элемент списка, поэтому используется анонимная переменная.
|
|
|
Пример 5.4. Реализуем операцию объединения двух множеств. Обозначается объединение множеств A и B через 
(рис. 5.1).
Рис. 5.1. Объединение множеств А и В. 
или 
.
Создадим предикат union, который зависит от трех аргументов: первые два – входные – данные множества, третий – выходной – результат объединения. Предикат проведем рекурсией по первому множеству. Базис индукции: объединение множества с пустым множеством есть исходное множество. Шаг рекурсии состоит из двух правил: 1) если 1-й элемент первого множествасодержится во втором множестве, то не добавлять этот элемент первого множества в результирующее множество, он попадет туда из второго множества; 2) если 1-й элемент первого множества не входит во второе множество, то добавить 1-й элемент первого списка результирующее множество.
union([],L,L). % объединение с пустым мн-вом
% есть само множество L.
union([H|T],L,L1):- % если голова 1-го множества
member_new(H,L),! % принадлежит 2-му множеству,
union(T,L,L1). % то объединить хвост 1-го
% множества со 2-м множеством.
union([H|T],L,[H|L1]):-
union(T,L,L1). % иначе объединить голову 1-го
% мн-ва и хвост, полученный
% объединением хвостов 1-го
% и 2-го множеств
При задании, например, цели
goal
union([1,2,3,6],[3,6,7,10],L).
получим множество[1,2,3,4,5].
Пример 5.5. Реализовать операцию пересечения двух множеств. Обозначается пересечение множеств A и B через 
(рис. 5.2).
Рис. 5.2.Пересечение множеств A и B. 
и
Создадим предикат intersection, который зависит от трех аргументов: первые два – входные – данные множества, третий – выходной – результат пересечения (элементы, которые входят и в первое, и во второе множествоодновременно). Этот предикат также проведем рекурсией по первому множеству. Базис рекурсии: пересечение любого множества с пустым множеством есть пустое множество. Шаг рекурсии состоит из двух правил: 1) если первый элемент 1-го множества является элементом 2-го множества, то пересечение множеств получается добавлением головы 1-го множества к пересечению хвоста 1-го множества со 2-м множеством; 2) если первый элемент 1-го множества не содержится во 2-м множестве, результат получается пересечением хвоста 1-го множества со 2-м множеством.
|
|
|
intersection([],_,[]). % пересечение пустого мн-ва с
% любым мн-вом есть пустое мн-во
intersection([H|T1],L,[H|T]):-
member_new(H,L),!, % если голова 1-го мн-ва
% содержится во 2-м мн-ве,
intersection(T1,L,T). % то получим пересечение
% добавлением головы 1-го мн.
% к пересечению хвоста
% 1-го мн-ва со 2-м мн-вом
intersection([_|T],L,L1):-
intersection(T,L,L1). % если голова 1-го мн-ва
% не содержится во 2-м мн-ве,
% то пересечь хвост 1-го
% мн-ва со 2-м мн-вом
При задании, например, цели
goal
intersection ([1,2,3,6],[3,6,7,10],L).
получим множество[3,6].
Пример 5.6. Реализовать операцию разности двух множеств. Разностьмножеств А и В – это множество, образованное элементами множества А, не принадлежащими множеству В.
Обозначается разность множеств A и B через A \ B. 
и 
.
а) 
б)
Рис. 5.3.Разность множеств а) A и B; б) В и А.
Из данного определения видно, что для получения разности множеств, важен их порядок, т. е. если A ={8,10,12,14}, B ={11,12, 13,14,15}, то A \ B ={8,10}, но B \ A ={11,13,15}.
Создадим предикат difference, который зависит от трех аргументов: первые два – входные, третий – выходной – результат разности множеств. Предикат проведем рекурсией по первому множеству. Базис рекурсии: если из пустого множества отнять любое множество, то получим пустое множество. Шаг рекурсии состоит из двух правил: 1) если первый элемент 1-го множества принадлежит 2-му множеству, то результат – это разность хвоста 1-го множества и 2-го множества; 2) если первый элемент 1-го множества не встречается в вычитаемом множестве, ответом будет множество, образованное приписыванием головы первого множества к результату вычитания второго множества из хвоста первого множества.
difference([],_,[]). % разность пустого мн-ва с любым
% мн-вом есть пустое множество
difference([H|T],L,L1):-
member_new(H,L),!, % если голова H 1-го мн-ва
% принадлежит 2-му мн-ву L,
difference(T,L,L1). % результатом L1 будет разность
% хвоста Т 1-го мн-ва и 2-го мн.
difference([H|T],L,[H|L1]):-
difference(T,L,L1). % иначе результат есть мн-во,
% образованное головой Н 1-го мн-ва и хвостом,
|
|
|
% полученным вычитанием из хвоста 1-го мн-ва T 2-го мн-ва L
Используя тождество = A \(A \ B), операцию пересечения можно представить в виде:
intersection_new(A,B,S):-
difference(A,B,A_B), % A_B=A\B
difference(A,A_B,S). % S = A\A_B = A\(A\B)
Пример 5.7. Реализовать предикат, позволяющий проверять, является ли одно множествоподмножеством другого.
Множество A является подмножеством множества B (
), если каждый элемент множества A содержится в множестве B. 
.
Построим предикат subset, который будет зависеть от двух входных параметров (множества А и В). Решение носит рекурсивный характер. Базис рекурсии: пустое множество есть подмножество любого множества. Шаг рекурсии: проверить, что первый элемент 1-го множества принадлежит 2-му множеству и хвост 1-го множества есть подмножество 2-го множества.
subset([],_).
subset([H|T],L):-
member_new(H,L),
subset(T,L).
Так как 
или 
, то предикат, выясняющий, является ли множество А подмножеством множества В, можно записать через операции объединения или пересечения:
subsetU(A,B):–
union(A,B,B). % через операцию объединения
subsetI(A,B):–
intersection(A,B,A). % через операцию пересечения
Предикат subset можно использовать для проверки совпадения двух множеств, т.к. 
и 
. Т.е. два множества равны, если все элементы первого множества содержатся во втором множестве, и наоборот.
equal(A,B):– % множества A и B совпадают,
subset(A,B), % если мн-во A содержится в мн-ве B и
subset(B,A). % мн-во B содержится в мн-ве A
Если требуется проверить, является ли множество А собственным подмножеством множества В (
), то предикат будет иметь вид:
proper_subset(A,B):–
subset(A,B), % мн-во A есть подмн-во B
not(equal(A,B)). % множества A и B не совпадают
Пример 5.8. Реализовать на Прологе операцию симметрической разности множеств А и В.
Симметрическая разность множеств А и В обозначается A Δ B и определяется: 
или 
. При этом A Δ B = B Δ A.
Рис. 5.4.Симметрическая разность множеств А и В.
Симметрическую разность можно выразить через разность и объединение множеств: 
. Поэтому процедура будет иметь вид:
sym_difference(A,B,SM):–
difference(A,B,A_B), % A_B – разность мн-в A и B
difference(B,A,B_A), % B_A – разность мн-в B и A
|
|
|
union(A_B,B_A,SD). % SD – результат
Пример 5.9. Реализовать на Прологе операцию дополнения.
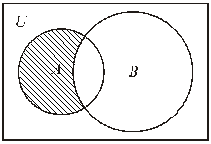
Дополнение множества A обозначается 
и определяется 
.
Рис. 5.5.Дополнение множества А (U – универсальное множество).
Воспользуемся тождеством = U \ A, где U – универсальное множество. Тогда на Прологе данная процедура имеет вид:
supp(A,D):–
U=[0,1,2,3,4,5,6,7,8,9], % задано универсальное мн.
difference(U,A,D). % D – разность универсального
% мн-ва U и мн-ва A
Имея дополнение, можно программно реализовать законы де Моргана 
, 
.
unionI(A,B,AB):–
supp(A,AD), % AD – дополнение мн-ва A
supp(B,BD), % BD – дополнение мн-ва B
intersection(A_,BD,A_B), % A_B – пересечение AD и BD
supp(A_B,AB). % AB – дополнение мн-ва A_B
intersectionU(A,B,AB):–
supp(A,AD), % AD – дополнение мн-ва A
supp(B,BD), % BD – дополнение мн-ва B
union(AD,BD,A_B), % A_B – объединение мн-в AD и BD
supp(A_B,AB). % AB – дополнение мн-ва A_B
Варианты заданий
1. Создать предикат, находящий все элементы в заштрихованной области (множества U, A, B, C задать самостоятельно):
2. Создать предикат, порождающий всевозможные перестановки исходного множества.
3. Создать предикат, порождающий всевозможные подмножества исходного множества.
4. Создать предикат, вычисляющий число элементов в заштрихованной области (множества U, A, B, C задать самостоятельно):
|
|
|
