 |
Составные части системы. Пр-ло фаз. Диаграмма состояния воды.
|
|
|
|
Направленность ковалентной связи. Сигма и пи-связи. Гибридизация атомных орбиталей.
Т.к.атомные орбитали пространственно ориентирован,
То перекрывание электр.облаков происходит по опред.направл-ям,что обуславливает направл-ть ков.св. Направл-ть выраж-ся в виде валентных углов м/у направл-ми х.св.в мол-ах и тв.телах.
Перекрывание облаков при образовании к.с. возможно только при определенной их взаимной ориентации в пространстве – отсюда направленность связей, приводящая к определенной форме молекул.
Сигма связь- связь,образов.перекрываением АО по линии,соедин.ядра взаимодейств.атомов.
П-связь- связь,образов.перек-ем АО по обе стороны линии,соед-ей ядра атомов(боковое перекр-е)
s-эл-ты могут образ-ть только Ϭ св.,р-эл-ты- Ϭ и π св.
При наложении 2ух π св. на Ϭ св.возникает тройная св.
Если в молекуле имеется кратная связь между атомами (двойная или тройная), то только одна связь является прочной - пи-связь. Остальные – сигма-связи.
Пример. Рассмотрим молекулу этилена (С2Н4).
Имеет место неполная гибридизация 
Между атомами углерода одна из связей «пи». Все остальне – «сигма».
Гибридизация: после гибр-и кол-во гибридных орбит-ей равно к-ву подвергшихся гибр-и.Гибр-и подвергаются близкие по энергии орбитали.
sp3: 109◦28 (CH4,SiH4)
sp2:120(BCl3,AlF3)
sp:180(ZnCl2,BeF2)
Константа химического равновесия. Расчет Кр и Кс.
Рассмотрим гомогенную химическую реакцию: 
Реакции протекают до полного исчезновения исходных веществ, а останавливаются при достижении определенного состояния равновесия. Условия химического равновесия: 
Равновесные давления участников реакции: 
Согласно закону действующих масс 
константа равновесия, выраженная через парциальные давления. Размерность 
. 
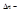изменение числа молей при протекании реакции.
|
|
|
При написании констант равновесия гетерогенных реакции учитываются парциальные давления только газообразных участников реакций, поскольку давления пара конденсированных фаз малы по сравнению с газообразными компонентами.
Пример. 
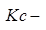константа равновесия, выраженная через концентрации.
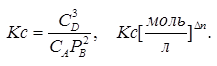
Кроме того существуют 
где а-активности, н-мольная доля.
Соотношения между константами равновесия:
Сильные электролиты. Понятие активности и коэффициента активности.
Электролиты – вещества, которые в растворе или расплаве состоят полностью или частично из ионов.
Сильные диссоциируют полностью – процесс необратим. Процесс диссоциации слабых обратим (в растворах содержатся как ионы, так и недиссоциированные молекулы).
К сильным электролитам относ-ся почти все соли,к-ты(азотная,серная,галогенводород.,хлорная),гидроксиды щелочн.ме.
В сильн.элетролитах нельзя искл-ть ионного взаим-я в р-ре,поэтому вводятся понятися «аквтисность иона»,как эффективности иона и неактивного иона.
a=f*c
В оч.сильных разбавленных электролитах коэф-т активности стремится к 0, а=с,т.е.полностью проявл-ся без образ-я ионных пар.
Если р-р концентрир.,то происходит броун.дв-е,ионные пары обр-ся и коэф-т акт-ти уменьш-ся.
В сильных неразбавл.электр-ах обр-ся ионные пары,поэтому за счет ионных пар коэф-т активности и конц-я уменьш.
Ионная сила р-ра вводится для х-ки активности:
По в-не ионной силы р-ра находяи коэф-т акт-ти в табл.и высчитывается акт-ть иона.Эта акт-ть иона заменяет конц-ю во всех ф-лах.
Составные части системы. Пр-ло фаз. Диаграмма состояния воды.
Сущность:
На основании эксперемент.данных стоят диаграмму сост-я сист.,выражающ.завис-ть к.-л. физич.состава сист(т-ра пл-я,твердость,пл-тьэлектропровод-ть)в виде ф-и её физич.состава.
|
|
|
Для метал.сист.особое знач-е имеет построение диагр. плавкости,что позволяет опр-ть появляющ-ся в сист.нов.фазы.
Составные части системы – химически индивидуальные вещества, составляющие данную систему и способные к самостоятельному существованию.
В равновесной системе 
имеются 3 составных части.
Константа равновесия: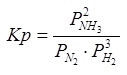 
Если известны парциальные давления двух участников реакции, система определена.
Независимые компоненты – индивидуальные вещества, наименьшее число которых необходимо и достаточно для образования всех фаз системы.
Число независимых компонентов – разница между числом составных частей и числом связывающих уравнений.
В данном примере: 3-1=2.
Степени свободы – независимые переменные, которые можно произвольно менять, не нарушая состояния системы (числа и характера фаз).
Правило фаз позволяет определить число фаз в системе при равновесии и изменение этого числа при изменении какого-либо параметра.
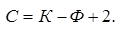С – число степеней свободы, К – компоненты, Ф – фазы.
Если 
и 
выражение 
Пример. Определить кол-во фаз в системе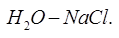 
С=К-Ф+2=4-Ф. Максимальное число фаз=минимум С.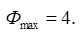 
Диаграмма состояния системы - диаграмма, указывающая, в каких фазовых состояниях находится система в зависимости от условий: температура, давление и состав.
В качестве системы возьмем воду. K=1 => состав как переменная отпадает, и фактически имеем Р-Т диаграмму.
С=К-Ф+2=3-Ф; максимальное число фаз, находящихся в равновесии, равно 3.
1 - поле СОВ-область существования твердой фазы – льда.
2 – СОА – жидкая фаза –вода.
3 – АОВ – водяной пар.
Если число ст.св.0,то 3 фазы.
Если число ст.0,то 2 фазы.
Если число ст.2,то 1 фаза.
Двувариантная сист.-
Одновариант.сист.-
ОС-повыш-е давл-я вызывает пониж-е т-ры,т.к.вызывает обр-е той фазы,к-ая обл-ет большей пл-ю.
|
|
|
