 |
Примеры вычисления пределов с подробным объяснением
|
|
|
|
Понятие предела функции
Сначала разберёмся, чем числовая последовательность отличается от функции.
Рассмотрим числовую последовательность, заданную своей формулой и функцию, заданную алгебраически:
| Числовая последовательность | Числовая функция |

| 
|

| 
|
- для числовой последовательности 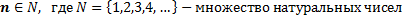
- для функции переменная  , где
, где  - множество действительных чисел. Это все числа, которые можно отобразить на числовой прямой, другими словами
- множество действительных чисел. Это все числа, которые можно отобразить на числовой прямой, другими словами 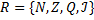 .
.
Имея алгебраическое выражение функции можно определить будет ли функция возрастающей, убывающей или периодической.
Функция будет возрастающей, если с увеличением значения  , значение функции
, значение функции  возрастает.
возрастает.
Например, функция  будет возрастающей, так как
будет возрастающей, так как 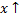
 :
:


| 

|
Функция будет убывающей, если с увеличением значения  , значение функции
, значение функции  уменьшается.
уменьшается.
Например, функция  будет убывающей, так как
будет убывающей, так как 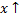
 :
:

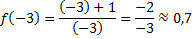
| 

|
Функция будет периодической, если для  , значение функции
, значение функции  повторяются.
повторяются.
Например, функция  будет периодической, с периодом
будет периодической, с периодом  , так как:
, так как:


| 
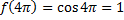
|
Определение предела функции
Если функция убывает или возрастает, то она стремится к конечному значению, которое называется пределом функции.
Определение: Число А называется пределом функции  при стремлении
при стремлении  .
.
Запись предела функции
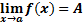
Теоремы о пределах
Т1. Предел постоянного числа равен этому числу 
Т2. Постоянное число можно вынести за знак предела 
Т3. Предел суммы (разности) равен сумме (разности) пределов 
Т4. Предел произведения равен произведению пределов 
Т5. Предел отношения равен отношению пределов 
Т6. Предел степени с натуральным показателем равен степени самого предела 
Примеры вычисления пределов с подробным объяснением
|
|
|
При вычислении пределов сначала нужно применить теоремы, а затем уже подставить число, к которому стремится  .
.

В примере №2 мы встречаем произведение числа «3» на «минус бесконечность». Нужно запомнить, что если  умножить или разделить на число, то получим всё равно
умножить или разделить на число, то получим всё равно  . Если к
. Если к  прибавить (вычесть) число, то так же получим
прибавить (вычесть) число, то так же получим  .
.



В примере №5 нельзя буквально считать, что мы делим на нуль. Нужно помнить, что  только стремится к нулю, но не равен ему. Это значит, что мы делим число «3» на число очень малой величины (близкое к нулю). При этом, чем оно меньше, тем результат деления больше (т.е. приближается к бесконечности). Не забываем про «минус» перед дробью.
только стремится к нулю, но не равен ему. Это значит, что мы делим число «3» на число очень малой величины (близкое к нулю). При этом, чем оно меньше, тем результат деления больше (т.е. приближается к бесконечности). Не забываем про «минус» перед дробью.

В примере №6 наоборот, мы должны разделит число «3» на бесконечно большое число (т.е., разделить на бесконечность). И чем больше делитель, тем ближе результат деления к нулю.


В примере №8 мы встречаем степень «плюс-минус бесконечности». Чётная и нечётная степень действует только на знаки «плюс и минус» по известному правилу: чётная степень убирает знак «минус»; нечётная степень сохраняет знак «минус». А степень бесконечности равна бесконечности.

Рассмотрим пример с нечётной степенью:

Для вычисления предела тригонометрических функций используем таблицу их значений.
Числовой множитель аргумента функции не выносится за знак предела.

Если в таблице значений для 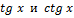 стоит прочерк, то данные функции нужно выразить через синус и косинус по формулам
стоит прочерк, то данные функции нужно выразить через синус и косинус по формулам 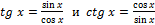
Например, для функции  . В таблице значений для тангенса
. В таблице значений для тангенса  стоит прочерк (т.е. тангенс такого значения не существует). Поэтому при вычислении предела нужно тангенс выразить через синус и косинус. Постоянный множитель «7» выносим перед знаком предела. Числовой множитель аргумента - число «3» оставляем на месте.
стоит прочерк (т.е. тангенс такого значения не существует). Поэтому при вычислении предела нужно тангенс выразить через синус и косинус. Постоянный множитель «7» выносим перед знаком предела. Числовой множитель аргумента - число «3» оставляем на месте.

В примере №12 встречаются в одном пределе и число, и переменная  , и тригонометрическая функция. В таких примерах для тригонометрической функции находим значение в таблице, а для переменной
, и тригонометрическая функция. В таких примерах для тригонометрической функции находим значение в таблице, а для переменной  подставляем вместо
подставляем вместо  число 3,14 (это приближённое значение).
число 3,14 (это приближённое значение).
|
|
|

Самостоятельная работа №1 «Предел функции»

| 
| 
| 
|

| 
| 
| 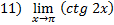
|

| 
| 
| 
|
Таблица значений тригонометрических функций
| I чт. | II чт. | III чт. | IV чт. | ||||||||||||||
 ,
град. ,
град.
| 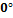
| 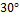
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 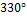
| 
|
 ,
рад. ,
рад.
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 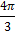
| 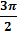
| 
| 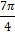
| 
| 
| |

| 
| 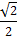
| 
| 
| 
| 
| -1 | 
| 
| 
| 
| 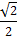
| 
| ||||

| 
| 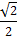
| 
| 
| 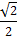
| 
| 
| 
| 
| -1 | 
| 
| 
| ||||

| 
| 
| -- | 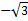
| 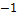
| 
| 
| 
| -- | 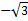
| 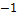
| 
| |||||

| -- | 
| 
| 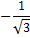
| 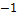
| 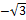
| -- | 
| 
| 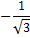
| 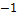
| 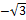
| -- |
|
|
|


