 |
Эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частот (интервальный вариационный ряд).
|
|
|
|
Пусть эмпирическое распределение задано в виде последовательности интервалов  и соответствующих им частот
и соответствующих им частот  (
( —сумма частот, которые попали в
—сумма частот, которые попали в  -й интервал):
-й интервал):
Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность  распределена нормально.
распределена нормально.
Для того чтобы при заданном уровне значимости  проверить гипотезу о нормальном распределении генеральной совокупности, надо:
проверить гипотезу о нормальном распределении генеральной совокупности, надо:
1. Вычислить выборочную среднюю  и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение  , причем в качестве вариант
, причем в качестве вариант  принимают среднее арифметическое концов интервала:
принимают среднее арифметическое концов интервала:

2. Пронормировать  , т. е. перейти к случайной величине
, т. е. перейти к случайной величине  и вычислить концы интервалов:
и вычислить концы интервалов:  ,
,  , причем наименьшее значение
, причем наименьшее значение  , т. е.
, т. е. 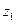 , полагают равным
, полагают равным  , а наибольшее, т. е.
, а наибольшее, т. е.  , полагают равным
, полагают равным  .
.
3. Вычислить теоретические частоты
 ,
,
где  — объем выборки (сумма всех частот);
— объем выборки (сумма всех частот);  — вероятности попадания
— вероятности попадания  в интервалы
в интервалы  ;
;  — функция Лапласа.
— функция Лапласа.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
c. составляют расчетную таблицу, по которой находят наблюдаемое значение критерия  ;
;
d. по таблице критических точек распределения  , по заданному уровню значимости
, по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы  (
( — число групп выборки) находят критическую точку
— число групп выборки) находят критическую точку  правосторонней критической области.
правосторонней критической области.
Если  — нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). Если
— нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно). Если 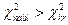 — гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
— гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
Малочисленные частоты ( ) следует объединить; в этом случае и соответствующие им теоретические частоты также надо сложить. Если производилось объединение частот, то при определении числа степеней свободы по формуле
) следует объединить; в этом случае и соответствующие им теоретические частоты также надо сложить. Если производилось объединение частот, то при определении числа степеней свободы по формуле  следует в качестве
следует в качестве  принять число групп выборки, оставшихся после объединения частот.
принять число групп выборки, оставшихся после объединения частот.
|
|
|
1.12.3 Проверка гипотезы о показательном распределении генеральной совокупности по критерию Пирсона
Пусть задано эмпирическое распределение непрерывной случайной величины  в виде последовательности интервалов
в виде последовательности интервалов  и соответствующих им частот
и соответствующих им частот  причем
причем  (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина
(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина  имеет показательное распределение.
имеет показательное распределение.
Для того чтобы при уровне значимости  проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю  . Для этого приняв в качестве «представителя»
. Для этого приняв в качестве «представителя»  -го интервала его середину
-го интервала его середину  , составляют последовательность равноотстоящих вариант и соответствующих им частот.
, составляют последовательность равноотстоящих вариант и соответствующих им частот.
2. Принять в качестве оценки параметра  показательного распределения величину, обратную выборочной средней:
показательного распределения величину, обратную выборочной средней:
 .
.
3. Найти вероятности попадания  в частичные интервалы
в частичные интервалы  по формуле
по формуле
 .
.
4. Вычислить теоретические частоты:
 ,
,
где  — объем выборки.
— объем выборки.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы  , где
, где  — число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то
— число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то  — число интервалов, оставшихся после объединения.
— число интервалов, оставшихся после объединения.
1.12.4 Проверка гипотезы о биномиальном распределении генеральной совокупности по критерию Пирсона
Произведено  опытов. Каждый опыт состоит из
опытов. Каждый опыт состоит из  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  одна и та же. Регистрируется число появлений события
одна и та же. Регистрируется число появлений события  в каждом опыте. В итоге получено следующее распределение дискретной случайной величины
в каждом опыте. В итоге получено следующее распределение дискретной случайной величины  — числа появлений события
— числа появлений события  (в первой строке указано число
(в первой строке указано число  появлений события
появлений события  в одном опыте; во второй строке — частота
в одном опыте; во второй строке — частота  , т. е. число опытов, в которых зарегистрировано
, т. е. число опытов, в которых зарегистрировано  появлений события
появлений события  ):
):
|
|
|

| 
| 
| ||

| 
| 
| 
| 
|
Требуется, используя критерий Пирсона, проверить гипотезу о распределении дискретной случайной величины  по биномиальному закону.
по биномиальному закону.
Для того чтобы при уровне значимости  проверить гипотезу о том, что дискретная случайная величина
проверить гипотезу о том, что дискретная случайная величина  (число появлений события
(число появлений события  ) распределена по биномиальному закону, надо:
) распределена по биномиальному закону, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю  .
.
2. Принять в качестве оценки параметра  биномиального распределения величину:
биномиального распределения величину:
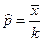 .
.
3. Найти по формуле Бернулли вероятности  появления ровно
появления ровно  событий
событий  в
в  испытаниях
испытаниях
 .
.
4. Вычислить теоретические частоты:
 ,
,
где  — объем выборки.
— объем выборки.
5. Сравнить эмпирические и теоретические частоты по критерию Пирсона, приняв число степеней свободы  (если вероятность
(если вероятность  появления события
появления события  задана, т. е. не оценивалось по выборке);
задана, т. е. не оценивалось по выборке);  (если же вероятность
(если же вероятность  была оценена по выборке).
была оценена по выборке).
Если было произведено объединение малочисленных частот, то  — число групп выборки, оставшихся после объединения частот.
— число групп выборки, оставшихся после объединения частот.
1.12.5 Проверка гипотезы о равномерном распределении генеральной совокупности по критерию Пирсона
Пусть задано эмпирическое распределение непрерывной случайной величины  в виде последовательности интервалов
в виде последовательности интервалов  и соответствующих им частот
и соответствующих им частот  , причем
, причем  (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина
(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина  распределена равномерно.
распределена равномерно.
Для того чтобы проверить гипотезу о равномерном распределении  , т. е. по закону
, т. е. по закону

надо:
1. Вычислить выборочную среднюю  и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение  (если объем выборки невелик, то лучше взять «исправленное» среднее квадратическое отклонение
(если объем выборки невелик, то лучше взять «исправленное» среднее квадратическое отклонение  ).
).
2. Оценить параметры  и
и 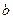 — концы интервала, в котором наблюдались возможные значения
— концы интервала, в котором наблюдались возможные значения  , по формулам (через
, по формулам (через  и
и  обозначены оценки параметров):
обозначены оценки параметров):
 ,
,  .
.
3. Найти плотность вероятности предполагаемого распределения
 .
.
4. Найти теоретические частоты:
 ;
;
 , (
, ( );
);
 .
.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы  , где
, где  — число интервалов, на которые разбита выборка.
— число интервалов, на которые разбита выборка.
|
|
|
1.12.6 Проверка гипотезы о распределении по закону Пуассона генеральной совокупности по критерию Пирсона
Пусть задано эмпирическое распределение дискретной случайной величины  . Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона.
. Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона.
Для того чтобы при уровне значимости  проверить гипотезу о том, что случайная величина
проверить гипотезу о том, что случайная величина  распределена по закону Пуассона, надо:
распределена по закону Пуассона, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю  .
.
2. Принять в качестве оценки параметра к распределения Пуассона выборочную среднюю:

3. Найти по формуле Пуассона вероятности  появления ровно
появления ровно  событий в
событий в  испытаниях (
испытаниях ( — объем выборки)
— объем выборки)
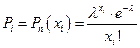 .
.
4. Вычислить теоретические частоты:
 .
.
5. Сравнить эмпирические и теоретические частоты по критерию Пирсона, приняв число степеней свободы  , где
, где  — число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то
— число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то  — число оставшихся групп).
— число оставшихся групп).
1.12.7 Критерий Колмогорова
Критерий Колмогорова предназначен для сопоставления эмпирического распределения с теоретическим. Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если в методе хи-квадрат мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т.д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия Колмогорова включается эта разность. Чем больше эмпирическое значение 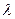 , тем более существенны различия.
, тем более существенны различия.
|
|
|
В критерии Колмогорова в качестве меры расхождения между двумя распределениями используется статистика
 .
.
Вычисляемый критерий:
Критерием является максимальное значение модуля разности между накопленными эмпирическими частотами 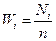 и соответствующими теоретическими частотами
и соответствующими теоретическими частотами  :
:

Интерпретация.
Пусть  — уровень значимости,
— уровень значимости, 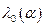 — критическое значение,
— критическое значение,  — объем выборки.
— объем выборки.
§ Двусторонняя критическая область:  против
против  .
.
Если  , то гипотеза
, то гипотеза  принимается, в противном случае — отвергается.
принимается, в противном случае — отвергается.
Критические точки распределения Колмогорова:

| 0,40 | 0,3 | 0,2 | 0,100 | 0,050 | 0,025 | 0,010 | 0,005 | 0,001 | 0,0005 |
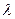
| 0,89 | 0,97 | 1,07 | 1,22 | 1,36 | 1,48 | 1,63 | 1,73 | 1,95 | 2,03 |
|
|
|


