Движение твердой частицы в произвольно расположенной трубе.

Рассмотренная упрощенная схема движения изолированной твердой частицы в вертикальном трубопроводе при восходящем выровненном потоке в действительности выглядит значительно более сложно.

Ясное выявление механизма движения твердых частиц в трубопроводах любого положения (вертикальных, наклонных, горизонтальных) имеет важное теоретическое и практическое значение.

Характер этого движения определяет выбор скорости транспортирования, расчет потерь давления, износ оборудования и другие параметры, определяющие строительные и эксплуатационные качества пылесосной установки. Движение твердых частиц происходит за счет энергии воздушного потока, получаемой от воздуховсасывающего агрегата. Это воздействие в виде аэродинамической силы зависит от относительной скорости и характера потока, а также от размеров и формы твердых частиц.

Наиболее простой и убедительной представляется гипотеза плоского параболического скачкообразного движения изолированной твердой частицы в горизонтальном трубопроводе (рис. 2). Под действием направленной по оси движения потока аэродинамической силы и направленной вниз силы тяжести твердая частица движется по параболе, выпадает из потока и катится по дну трубопровода.

 

 

 

1. 2. 3.

Рис. 2. Движение твердой частицы по трубопроводу

1 – линейное; 2 – скачкообразное; 3 – винтовое.

 

Шаг такого скачка в зависимости от соотношения действующих сил может быть весьма большим, и на коротком участке траектория может показаться линейной. При возрастании скорости качения, а также ввиду значительного градиента скорости у стенки трубопровода может возникнуть подъемная сила, в результате чего частица взлетит и снова совершит параболический полет. Причиной подъема также может быть упругий удар твердой частицы о стенку трубопровода.

На твердую частицу, двигающуюся в трубопроводе, в общем случае могут действовать три силы: совпадающая с осевым направлением движением потока аэродинамическая сила Т, направленная вниз сила тяжести G и направленная к стенкам трубопровода центробежная сила С.

Центробежная сила может возникнуть при вращательном движении потока, увлекающего за собой и твердые частицы.

Винтовое движение потока является более сложным случаем, и возможность его существования доказана теоретически. В трубопроводах всегда имеется источник скоса потока, порождающего устойчивое движение потока (закручивание). Известно, например, что в изгибе потока возникает парный вращающий вихрь. Эксперименты показали, что за такими распространенными местными сопротивлениями, как дроссель, тройник, поток начинает устойчиво винтообразно вращаться.

В том случае, когда центробежная сила больше силы тяжести и достаточна для прижатия твердой частицы к стенкам трубопровода, траектория движения частицы представляет собой пространственную винтообразную линию, т. е. движение ее вращательное. Такое движение, например, специально осуществляется в центробежных пылесосах циклонного типа.

При низкой величине центробежной силы движение будет иным. Преобладание силы тяжести будет характеризоваться протаскиванием твердых частиц по дну трубопровода, а преобладание аэродинамической силы – практически линейным движением (по пологой параболе) твердых частиц по всему сечению трубопровода.

При винтовом движении по сравнению с плоским можно меньше опасаться выпадения твердых частиц и засорения трубопровода, а, следовательно, можно принимать меньшие скорости транспортирования. При этом, однако, будут относительно большие потери давления в трубопроводе и большая величина износа.

 

Критерий прижатия.

Для расчетного выявления формы движения твердых частиц в трубопроводах (плоской или винтовой), которая, как указывалась выше, имеет решающее практическое значение, автором рекомендуется применение критерия прижатия (рис. 20).

Твердая частица будет двигаться по винтовой линии вдоль стенок трубопровода в том случае, если в наименее благоприятном для нее положении (в верхней части трубопровода) центробежная сила окажется больше радиальной составляющей силы тяжести, т. е. С>G.

Центробежная сила

, (3.2.8)

где m – масса твердой частицы, приведенная к ускорению свободного падения в кг×с²/м;

v_R – скорость движения твердой частицы в м/с;

R – радиус поперечного сечения трубопровода в м.

При движении твердой частицы вдоль стенок трубопровода по винтовой линии из треугольника скоростей (рис. 3) следует

, (3.2.9)

где v_k – скорость движения твердой частицы в м/с;

e_k – угол скоса движения твердой частицы в град.

(3.2.10)

Вид сбоку Т Силы

b

У=m×g×сosb

	Рис. 3 - К определению критерия прижатия.

R m×g b

 

 

Вид сверху

V_кsine_к=V_R V_к

e_к Скорости

 

После подстановки в формулу центробежная сила

. (3.2.11)

Радиальная составляющая силы тяжести

, (3.2.12)

где g – ускорение свободного падения в м/с²;

b - угол наклона трубопровода к горизонту в град.

Отношение этих двух сил представляет собой безразмерную величину, называемую (после сокращения на m) критерием прижатия:

. (3.2.13)

Если К_п > 1, то центробежная сила больше силы тяжести и имеет место винтовое движение, а если К_п < 1, то сила тяжести больше центробежной и имеет место плоское движение. К_п определяется в зависимости от взаимоотношения сил тяжести и центробежной (при этом влияние массы устраняется), но, очевидно, также зависит и от аэродинамической силы, так как входящие в него значения v_R и v_k обусловливаются скоростью и характером движения транспортирующего потока, размером и формой твердых частиц.

Физическое значение предложенного критерия не расходится с его математической формой. Например, если вращения потока нет и движение твердых частиц явно плоское, то e_к = 0 и sine_k = 0, а значит и К_п < 1 (К_п = 0).

Если трубопровод вертикальный, то за счет отсутствия стабилизирующего влияния радиальных составляющих силы тяжести возможно вращательное движение твердых частиц даже при самом ничтожном угле скоса. Действительно, в этом случае b = 90⁰ и cos90⁰ = 0, а значит К_п > 1 (К_п = ¥).

Возможность движения твердых частиц в трубопроводах, а следовательно, и возможность применения критерия прижатия, очевидно, должны иметь место только при конечных и положительных значениях v_k, R и g.

Значения v_k и e_к для твердых частиц при установившемся движении должны мало отличаться от v и e для переносящей эти частицы среды.

При этом v_n < v, но sine_к > sine, поэтому входящее в критерий прижатия произведение этих величин, а тем более во второй степени должно стремиться к уменьшению расхождения, т. е. допускается, что

(3.2.14)

и

. (3.2.15)

Значения R и b задаются геометрически при проектировании трубопровода.

Значение v при турбулентном движении и незначительных углах скоса приближенно может быть принято равной средней скорость движения через трубопровод, также обычно задаваемой при проектировании.

При этом следовало бы принять

, (3.2.16)

но при малых углах

. (3.2.17)

Значение e, как показали исследования, может быть вычислено по формуле

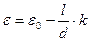, (3.2.18)

где e - угол наклона на данном удалении в град;

e₀ - угол наклона непосредственно за местным сопротивлением (устанавливается вне зависимости от скорости для каждого местного сопротивления опытным путем);

l – удаление в м;

d – диаметр трубопровода в м;

k @ 0,2 – коэффициент затухания, принимаемый из опыта.

Таким образом, критерий прижатия может быть вычислен и применен при расчете трубопроводов пылесосных установок.

Как уже указывалось, при вращательном движении можно принимать меньшие скорости транспортирования и меньшую мощность оборудования, чем при плоском движении, но иметь при этом большие потери давления и больший износ оборудования. Путем подбора исходных параметров, задаваемых при проектировании и учитываемых критерием прижатия, можно обусловливать любой характер движения твердых частиц и трубопроводах, а значит можно более рационально и экономично проектировать пылесосные установки.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: