 |
Энтропия изолированной термодинамической системы.
|
|
|
|
Изменение энтропии в обратимых процессов идеального газов. Изображение процессов в коорд S-T.
А) изохорный процесс
При V=const; dq= cvdT ds=dq/T=cvdT/T
Принимая cv=const после интегр. получим:
ΔS=cvcn T2/T1
Линия изохорного процесса в координатах S-T - логарифм кривая 1-2
| T |
| T |
| 3' |
| S |
V=const p=const
T1 1
1' 2'
В этом процессе dq=dU
Qv=Δ=пл. 1-2-2'-1'-1
Б) изобарный процесс
При p=const dq=CpdT
dS=dq/dT=QpdT/T
принимая Сp=const после интегрирования получим:
ΔS=CplnT2/T1;
Сравним выражения для измен. энтропии в изохорном и изобарном процессах
Т.к. Cp > Cv то в том же интервале темп. ΔSp > ΔSv и кривая изобарного пр-сса 1-3 пойдет более полого
qp=ΔU+l= пл.1-3-3'-1'-1
в) изотермический процесс:
При T=const
ΔS= 
=1/T 
=q/T …(*)
q=ΔU+l q=l=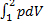 
= 
=RT
подставим в уравнение (*) получ. выр.
Получим:
ΔS=Rln V2/V1=Rln P2/P1
Из ур-ния (*) qT=T(S2-S1)=пл. 1-2-2'-1'-1
| T |
| T |
| 1’’’ |
| 2’ |
| S |
dq=0
Г) Адиабатный процесс
При dq=0 dS=dq/T=0 и ΔS=S3-S1=0
Следовательно обратимый адиабатный процесс- изоэнтропийный
При расшир. Газа процесс направлен сверху вниз т.к. работа соверш. за счет внутр. энергии, а при уменьш. внутренней энергии темп. газа понижается.
Д) Политропный процесс
Газ опред. энтропии dS=dq/T и ур-нии 1 з-на термод. Dq=CvdT + qdV
следует что dS=Cv*dT/T + P/T*dV
Получим ур-нием состояния pV=RT произведем замену P/T=R/V тогда
dS=CvdT/T + RdV/V (*)
После интегрирования получим
ΔS=S2-S1=CvlnT2/T1=R ln V1/V1 (2)
Из ур-ния состояния написанного в дтфференциальной форме
dV/V + dp/p + dT/T
подставим значение dT/T в ур-ние (2) тогда:
dS=CvdV/V + Cvdp/o + RdV/V= CpdV/V + Cvdp/p
|
|
|
после интегр. получим
ΔS=S2 – S1 = CvlnT2/T1 + R ln V2/V1 (1)
ΔS=S2 – S1 =CplnV2/V1 + Cv ln P2/P1 (2)
Подст. в ур-ние (2) значение dV/V=dT/T=dp/p
dS=CvdT/T + RdT/T – Rdp/p = CpdT/T – Rdp/p
после интегр. получим:
ΔS=S2 – S1 = CvlnT2/T1 + R ln P2/P1 (3)
Пользуясь ф-тами (1,2,3) можно получить выведенные ранее уравнения для ΔS в изохорном, изобарном и изотерм. процессах
dq=CdT C- тепл.политропн.процесса.
dS=dq/T=CdT/T и после интегр.
ΔS=S2 – S1 = CvlnT2/T1= Сv(n-k) (4)
Сравним изображение основных процессов в координатах ρ-T: v-p
Видно, что основные процессы изображены в координатах v-p линиями в корд. ρ-T изобр.кривыми и наоборот.
В процессах проходящих через 1 и 3 четверть теплоемкость С > 0, в процессе проходящих через 2 и 4 четверти С.
«7.12.82»Лекции № XIV
Обобщенный цикл Карно.
Рассмотрим обратимый цикл состоящий из двух изотерм 1-2 и 3-4 и произв.процессов 2-3 и 4-1 изображаемых эквидистантными линиями, для осуществления обратимых процессов 2-3 и 4-1 необходимо иметь беск.большое число источников теплоты с температурой от от T1Δ1 до Δ2 T2.Внешние источники теплоты можно заменить бесконечно большим числом регинераторов с помощью которой теплота отводимая от рабочего тела в одном процессе возвращается в рабочее тело в другом процессе.
В процессе 2-3 от рабочего тела отбирается и передается регинерат. количества теплоты qрег, а в процессе 4-1 такое же количество теплоты и при тех исл.температурнах возвращается от регинераторов к работе телу. Следовательно при полной регинерации теплоты, рассматриваемый цикл, как и цикл Карно соверш-ся между двумя источниками теплота с темп. T1 и Т2.
От источника в процессе 1-2 подводится теплота q1=T1*ΔS1.
Холодному источнику в процессе 3-4 передается теплота q2=T2*ΔS2 т.к. линии 2-3 и 4-1эквидистантны, то ΔS1=ΔS и термический КПД цикла:
Таким образом обратимый цикл с полной регинерацией теплоты имеет КПД равный КПД цикла Карно в том же интервале температур. Поэтому такой регинеративный цикл называется обобщенным циклом Карно.
|
|
|
Энтропия изолированной термодинамической системы.
Изолированная, в тепловом отношении, система не получает и не отдает теплоту во внешнюю среду, для неё dQ = 0.
Если в такой системе совершается обратимый процесс, то dS= 
= 0 и S1 = S2 если соверш.необратимый процесс, то dS > (dQ/T) необр., d Q = 0 поэтому dS > 0 и S2 > S1
Обобщая для изолированной системы можно написать: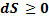 
Т.е.энтропия изолированной системы может оставаться неизменной (при обратимых процессах), может возрастать (при необратимых процессах), но никогда не может уменьшаться. Это положение относится ко всей системе в целом при этом энтропия отдельных тел может как возрастать, так и уменьшаться.
В качестве примера рассмотрим изолированную систему в которой протекает типичный необратимый процесс – передача теплоты при конечной разности температур.
|
|
|
