Портфельная теория Марковица

Введение

 

В последние годы в нашей стране в связи с развитием рыночной экономики существенно повысился интерес к постановке и решению задач теории инвестиций. Среди этих задач значительное место занимают задачи оптимизации портфелей активов.

Действительно, выбирая различные варианты распределения капитала между объектами, в которые инвестируется капитал, мы будем иметь различные результаты, если под результатом понимать величину дохода, полученного в течение заранее определенного периода. Очевидно, оптимальное распределение инвестируемого капитала должно обеспечивать в некотором смысле наилучший результат (приобрести недооцененные акции, чья рыночная цена на момент покупки ниже истинной, и избавиться от переоцененных бумаг и тем самым получить в перспективе максимальную прибыль). В то же время, решение о структуре распределения капитала принимается часто в условиях неопределенности, когда доходность от вложения капитала в объекты инвестирования носит случайный характер. Тем самым появляется риск вложения капитала и задача оптимизации портфеля инвестиций должна ставиться и решаться в условиях наличия риска.

Целью данного реферата является составление оптимального портфеля ценных бумаг, используя различные модели.

 

Теоретические аспекты формирования оптимального портфеля ценных бумаг

 

Если портфель состоит более чем из 2 ценных бумаг, то для любого заданного уровня доходности существует бесконечное число портфелей, или, иными словами, можно сформулировать бесконечное количество портфелей, имеющих одну и ту же доходность.

Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью E(r_n) необходимо найти такой, который обеспечивал бы минимальный уровень риска. Иными словами, можно задачу инвестора свести к следующему: необходимо найти минимальное значение дисперсии портфеля

 

(1)

 

при заданных начальных условиях:

 

(2)

(3)

 

Для решения задачи нахождения оптимального портфеля, содержащего n ценных бумаг, необходимо первоначально вычислить:

а) n значений ожидаемой доходности E(r_i), где i = 1, 2,…, n каждой ценной бумаги в портфеле;

б) n значений дисперсий σ_i 2 каждой ценной бумаги;

в) n (n-1)/2 значений ковариации σ_i 2, j, где i, j = 1, 2,…, n.

Если подставить значения E(r_i), σ_i и σ_i,j в выражения (1 -3), то выясняется, что в этих уравнениях неизвестными оказываются только величины W_i - «веса» каждой ценной бумаги в портфеле. Следовательно, задача формирования оптимального портфеля из n ценных бумаг по сути дела сводится к следующему: для выбранной величины доходности Е^* инвестор должен найти такие значения W_i, при которых риск инвестиционного портфеля становится минимальным. Иначе говоря, для выбранного значения Е^* инвестор должен определить, какие суммы инвестиционных затрат необходимо направить на приобретение той или иной ценной бумаги, чтобы риск инвестиционного портфеля оказался минимальным.

 

Метод Шарпа

 

В 1963 г. американский экономист У. Шарп предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа.

В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две переменные величины - независимую Х и зависимую Y линейным выражением типа Y = α + β Х. В модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи r_m, вычисленную на основе индекса Standart and Poor’s (S&P500). В качестве зависимой переменной берется отдача ri какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&P500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно

модель Шарпа называют рыночной моделью, а норму отдачи r_m - рыночной нормой отдачи.

Пусть норма отдачи r_m принимает случайные значения и в течение N шагов расчета наблюдались величины r_m1, r_mІ,…, r_mN. При этом доходность r_i какой-то i-ой ценной бумаги имела значения r_i1, r_i2,…, r_iN. В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами r_m и r_i в любой наблюдаемый момент времени в виде:

 

r_i,t = α_i + β_ir_m,t + ε_i,t    (4)

 

где: r_i,t - доходность i-ой ценной бумаги в момент времени t;

α_i - параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг r_m;

β_i - параметр линейной регрессии, называемый «бета», показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;

r_m,t - доходность рыночного портфеля в момент t;

ε_i,t - случайная ошибка, свидетельствующая о том, что реальные, действующие значения r_i,t и r_m,t порою отклоняются от линейной зависимости.

Особое значение необходимо уделить параметру β_i, поскольку он определяет чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности. Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:

 

(5)

 

где W_i - вес каждой ценной бумаги в портфеле

Дисперсия портфеля в модели Шарпа представляется в виде:

 

(6)

 

Цели инвестора сводятся к следующему:

необходимо найти минимальное значение дисперсии портфеля при следующих начальных условиях

 

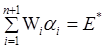(7)

(8)

(9)

 

Итак, отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:

) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности r_i,t каждой ценной бумаги.

) По рыночному индексу вычислить рыночные доходности r_m,t для того же промежутка времени.

) Определить величину дисперсии рыночного показателя σ_m, а также значения ковариаций σ_i,m доходностей каждой ценной бумаги с рыночной нормой отдачи и найти величины β_i:

 

 (10)

 

) Найти ожидаемые доходности каждой ценной бумаги E(r_i) и рыночной доходности E(r_m) и вычислить параметр α_i:

 

α_i = E(r_i) - β_iE(r_m) (11)

 

) Вычислить дисперсии σ²_ε,i ошибок регрессионной модели

) Подставить эти значения в соответствующие уравнения

После такой подстановки выяснится, что неизвестными величинами являются веса W_i ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля E^*, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель. [1]

Портфельная теория Марковица

 

Портфель Марковица минимального риска

Задача оптимизации портфеля активов с вектором средней доходности  ковариационной матрицей  может быть сформулирована следующим образом

 

 

К этим условиям в задаче оптимизации портфеля активов следует добавить условие положительности портфеля (долей). Однако, в общем случае финансовых инструментов предполагается возможность открытия коротких позиций (отрицательных долей инструментов в портфеле). Тогда можно найти общее аналитическое решение задачи. Если обозначить,

 

 

то решение задачи имеет вид

 

 

Тогда зависимость дисперсии оптимизированного (эффективного) портфеля от требуемой доходности будет иметь вид

 

 

где  - минимально возможная дисперсия доходности портфеля и соответствующая ему средняя доходность

 - доходность портфеля, с соотношением риск-доходность таким же как и портфель минимального риска (графически это единственная точка пересечения с параболой прямой, проходящей через начало координат и вершину параболы)

Поделиться:

Воспользуйтесь поиском по сайту: