Примеры решения задач К 2.1 – К 2.8

Решение задач жёсткости

 

Здесь рассматривается решение задач жесткости при растяже­нии-сжатии и кручении. Решение задач жесткости при изгибе и сложных ви­дах нагружения бу­дет рассмотрено во второй части курса.

Условие жесткости формулируется так: перемещение в задан­ной точке или сечении конструкции не должно превышать допусти­мых по условиям эксплуатации пере­мещений этой точки или сече­ния.

Математические выражения условий жесткости:

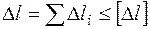– при растяжении-сжатии;

– при кручении.

Здесь 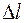– расчетное изменение длины расчетной схемы или её части; – расчетные изменения длины входящих в них участков; – расчетный угол закручивания расчетной схемы или её час­ти; – расчетные углы закручивания входящих в них участков; – отно­си­тельный угол закручивания; – допускаемые измене­ние длины, угол закру­чивания и относитель­ный угол закручивания.

В инженерной практике чаще всего решаются три типа задач жест­кости:

- проверка жесткости;

- определение размеров сечения, обеспечивающих за­данную жест­кость;

- определение допускаемой нагрузки, при которой обеспечива­ется жесткость конструкции.

Алгоритм решения этих задач включает следующие шаги:

1. Выбор и изображение расчетной схемы;

2. Построение эпюр внутренних силовых факторов;

3. Запись условия жесткости;

4. Определение в численном или алгебраическом виде , , вычис­ление , , .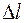

Рассмотрим содержание этих шагов.

Выбор и изображение расчётной схемы и построение эпюр вы­полня­ются аналогично соответствующим шагам в алгоритме реше­ния задач прочности.

Запись условия жёсткости – содержание этого шага раскрыто в п. 4.2.2.

Определение , , , , .

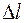На участках, где N = const, М_к = const:

, .

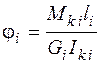На участках, где N ≠ const, М_к ≠ const:

, ,

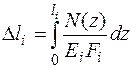где N(z), M_к(z) – аналитические выражения для определения N и М_к в произвольном сечении участка.

В качестве этих выражений можно использовать выражения, которые были составлены при построении эпюр.

Суммируя ∆l_i, получают выражение для ∆l, суммируя ∆ _i, полу­чают выражение для . Если условие жёсткости при кручении выра­же­но через , то записывают выражение для . Если рас­чет­ная схема состоит из стержней одного поперечного сечения, то в ка­честве М_к в выражение для подставляют максимальное по абсо­лют­ной величине значение, взятое с эпюры М_к.

Если в расчетной схеме есть участки с разными поперечными се­че­ниями, то выражение для составляют аналогично для каждого уча­стка.

Ответ на вопрос задачи. При проверке жесткости вычисляют численное значение ∆l, 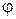, и сравнивают с [ ∆l ], [ ], [ ]. Если ∆l ≤ [ ∆l ], ≤ [ ], ≤ [ ], то тре­буемая же­сткость обеспечена, иначе не обеспечена.

При определении необходимых размеров или допускаемой на­грузки в условие жесткости вместо знака "≤" ставят знак "=".

Для определения размеров в полученное равенство подставляют F или I_k, выраженные через размеры сечения, затем разрешают его от­носительно размеров сечения.

При определении допускаемой нагрузки в равенство подстав­ляют N или М_к, вы­раженные через внешнюю нагрузку (если они не были уже выражены на этапе получения ∆l, , ), а затем разре­шают ра­венство относительно внешней на­грузки.

 

Примечание. Если задачи по определению размеров сечения или до­пускаемой нагрузки из условия жесткости решаются как самосто­ятельные, то после их решения в обязательном порядке необходима проверка прочности.

 

4.3. Методические указания к решению за­дач К 2.5, К 2.6

В задачах К 2.5 и К 2.6 требуется для сложных сечений вычис­лить значения главных центральных моментов инерции и опреде­лить по­ложение главных цен­тральных осей.

Алгоритм решения этих задач:

1. Вычерчивают сложное сечение.

2. Сложное сечение разделяют на простые составляющие части.

3. Выбирают начальные оси Х₀У₀.

4. Определяют координаты центров тяжести составляющих частей в системе координат Х₀У₀. Через их центры тяжести проводят цен­т­ральные оси составляющих частей, параллель­ные осям Х₀У₀. Вычис­ляют площади простых час­тей и их моменты инерции отно­сительно их центральных осей.

5. Определяют площадь и координаты центра тяжести всего сечения в системе координат Х₀У₀. Через центр тяжести сечения про­водят цен­тральные оси Х_сУ_с, параллельные осям Х₀У₀. Определяют моменты инерции сечения относительно этих осей.

6. Определяют главные центральные моменты инерции и по­ложение глав­ных центральных осей сечения.

Рассмотрим эти шаги более подробно.*

1-й шаг алгоритма. Сечение вычерчивается в произвольном масштабе на бумаге в кле­точку или миллиметровке. Чертеж должен занимать не менее поло­вины листа ученической тетради. На чертеже проставляют все размеры сечения, необходимые для расчета.

2-й шаг алгоритма. Простой будем называть часть сечения, для которой известны по­ло­жение центра тяжести, а также формулы для определения пло­щади и центральных мо­ментов инерции или их чи­словые значения. Для уменьшения числа составляющих частей, осо­бенно для сечений с вы­резами и отверстиями, допускается добавлять к сечению мнимые (от­сутствующие) части. В расчетах площади и моменты инер­ции мни­мых частей берутся с противоположным знаком, по сравнению со зна­ком аналогичных дейст­вительных час­тей. Простые части ну­ме­руют.

3-й шаг алгоритма. Решение можно выполнить с любыми про­извольно взятыми осями Х₀У₀ . Однако затрат труда будет меньше, если начальные оси естест­венным образом связать с сечением. Для сечений несиммет­ричных жела­тельно начальные оси на­правлять по границам сечения или простых частей. Желательно, чтобы всё сече­ние находилось в первой четверти. С целью устранения возможных ошибок рекомендуется выбирать только правую систему координат (ось У₀ направлена вверх, ось Х₀ – вправо). Для сечений симметрич­ных желательно, чтобы начальные оси сов­падали с осями симмет­рии.

4-й шаг алгоритма. При выполнении этого и пятого шага алго­ритма для снижения веро­ятности появления ошибок, повышения удобства проведения расче­тов, контроля и про­верки их правильно­сти, результаты расчетов за­носят в единую таблицу (табл. 12). Поря­док заполнения таблицы по­казан в п. 4.3.

__________________________________________________________ *Примеры практического использования алгоритма даны в разд. 4.4.

 

Таблица 12

Часть	хс,	ус	F	Ix	Iv	Ixy	a	b	a2F	b2F	abF
…
N
Сече­ние

 

Координаты центров тяжести определяют в системе координат Х₀У₀ с уче­том знаков. Для этого используют размеры на чертеже и зависи­мости, определяющие координаты центров тяжести простых частей. Через центры тяжести простых частей проводят их централь­ные оси, параллель­ные осям Х₀У₀. По известным формулам опреде­ляют пло­щади и моменты инерции простых частей относительно проведенных центральных осей. Если формулы для определения мо­ментов инер­ции даны для центральных осей, непараллельных осям Х₀У₀, то по­сле определения моментов инерции относительно этих осей опреде­ляют мо­менты инерции относительно центральных осей, параллель­ных осям Х₀У₀, исполь­зуя формулы для определения моментов инерции при повороте осей.

5-й шаг алгоритма. Определяют пло­щадь сечения F

,

где n – число простых частей; F_i – площадь i -ой части.

Координаты центра тяжести сечения опреде­ляют по формулам

; .

Здесь x_ci, у_ci – координаты цен­тра тяжести i- ой части в системе коор­динат Х₀У₀.

В сечениях, имеющих ось симметрии, центр тяжести находится на этой оси, в сечениях, имеющих две и более осей симметрии, – на пе­ресечении осей симмет­рии.

Отмечают на чертеже центр тяжести и проводят через него цен­т­ральные оси (Х_с , У_с) сечения, параллельные осям Х₀, У₀. Вычис­ляют моменты инер­ции сечения относительно проведенных цен­тральных осей по формулам

;

; (4.2)

.

Здесь а_i= (у_сi – у_с) – расстояние между центральной осью х_с i- ой части и центральной осью Х_c сечения; b_i= (x_сi – x_с) – рас­стояние между центральной осью у_с i- ой части и цен­тральной осью У_c сечения.

Рас­стояния а_i, b_i определяются с учетом знака.

Вычисляются , , 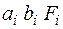для каждой части и заносятся в табл. 12. Затем находят , , , , , путем суммирова­ния данных, записанных в соответст­вующих столбцах табл. 12. Далее находят I_x(c), I_у(c), I_xу(c) по формулам (4.2).

Й шаг алгоритма.

Определяют главные центральные моменты инерции I_u, I_v сечения по фор­муле

.

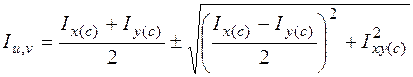При определении I_u перед корнем берут знак «плюс», при определении I_v – знак «минус».

Определяют угол a между осью Х_с и главной центральной осью u (осью, отно­сительно которой осевой момент инерции максимален)

.

На чертеже сечения проводят главные центральные оси. Под углом a к оси Х_с через центр тяжести сечения проводят ось u. Ось v проводят через центр тяжести перпендикулярно оси u.

Примеры решения задач К 2.1 – К 2.8

Задача К 2.1

Ступенчатый стержень (рис. 33) с площадями поперечных сече­ний F₁, F₂, F₃ нагружен осевыми силами P₁, P₂, P₃, приложенными по концам или в сере­дине участ­ков длиной b, с, d. Материал стерж­ня – сталь, допускае­мое на­пряже­ние [s]= 160 МПа, модуль упру­гости E = 2×10⁵ МПа.

Требу­ется построить эпюры нор­мальных сил, напряжений и пе­ре­ме­щений, оценить прочность стержня, определить про­цент пере- или недонап­ряжения.

Исходные данные к задаче: b = 50 см, с = 40 см, d = 80 см, F₁ = =25 см², F₂ = 18 см², F₃ = 10 см², P₁ = 70 кН, P₂ = 120 кН, P₃ = 80 кН.

 

Решение

1. Изображаем расчетную схему (рис. 34а). Обозна­чаем гра­ницы участ­ков и точки приложения сил бу­квами А, В, С, D, Е.

2. Строим эпюру " N " (рис. 34б).

3. Строим эпюру "s" (рис. 34в); .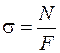

Так как на всех участках N = const, то иs = const.

При вычислениях значе­ния всех величин под­ставляем в формулы в ос­новных единицах СИ.

Уча­сток DE:

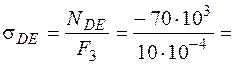-70×10⁶ Па = -70 МПа.

Уча­сток СD:

-38,8×10⁶ Па = -38,8 МПа.

Уча­сток ВС:

27,8×10⁶ Па = 27,8 МПа.

Уча­сток АВ:

-12×10⁶ Па = -12 МПа.

Для построения эпюры на границах участков откла­ды­ваем от нуле­вой ли­нии по­лучен­ные значения ²s²в масштабе с учетом знаков и соединяем их прямыми ли­ниями.

4. Строим эпюру пере­меще­ний (рис. 34г).

Перемещение сечения А равно нулю, так как это сече­ние за­креплено. Перемещение других сечений равно сумме изменения длин участков, расположенных между этими сечениями и задел­кой.

 

 

Рис. 34

 

 

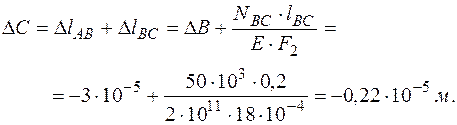
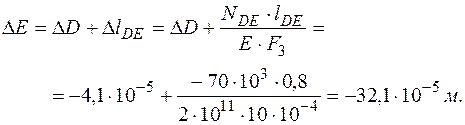
Откладывая от нулевой линии полученные значения перемещений в сече­ниях В, С, D, Е в масштабе с учетом знаков и соединяя полу­ченные точки прямыми линиями, получаем эпюру перемещений (показана на рис.34г).

5.Оцениваем прочность стержня, определяем процент пере- или не­донапря­жения.

Прочность стержня обеспечена, так как

s _max = 70 МПа < [s] = 160 МПа.

Стер­жень недонапряжен:

.

Недонапряжение составляет 56,2 % от [s].

 

Задача К 2.2

Эта задача является типичной задачей по определению необхо­ди­мых раз­меров поперечных сечений из условия прочности. Реша­ется она в соответствии с алгоритмом, рассмотренным в п. 4.2.

Изменение длины бруса определяется

,

где n – число участков на расчетной схеме, на которых F = const, N = const; – изменение длины i- го участка; F_i – площадь попе­речного сечения с размерами, определенными из условия прочности на данном участке.

 

 

Задача К 2.3

Условия задачи изло­жены в п. 4.1. Схема задачи изображена на рис. 35.

Исходные данные: М₁ =28 кН×м, М₂ = 22 кН×м, М₃ = 9 кН×м, М₄ = =12 кН×м, a =1 м, b =1,8 м, с = = 0,8 м, [ t ] = 50 МПа, [ q ] = =0,008 рад/м, G = 8×10⁴ МПа.

 

Решение

1.Определяем величину и на­прав­ление момента М₀.

Вал под действием приложенных к нему моментов должен нахо­дит­ся в рав­новесии, т.е. S М_z = 0.

При записи этого урав­нения моменты, направ­ленные против часо­вой стрелки, счи­таем поло­жительными, по часовой стрелке – от­рица­тель­ными. На­блюдение ве­дем с пра­вого конца вала.

S М_z = - М₄ + М₃ + +М₂ + М₀ + М₁ = -12 + +9+ 22 + М₀ +28 = 0,

М₀ = - 47 кН×м.

Знак "минус" при М₀ указывает на то, что этот момент в действи­тельности направлен противоположно указанному на схеме задачи.

2. Изображаем расчет­ную схему вала (рис. 36а). Точки приложения мо­ментов (границы уча­стков) обозначаем бук­вами А, В, С, D, Е.

3. Строим эпюру " М_к " (рис. 36б).

4. Определяем необходимый диаметр вала

а) из условия прочности

,

М_к.расч = 28 кН×м (берем с эпюры М_к).

.

Приравнивая выражение для t _max и [t], получим:

,

откуда

м.

б) из условия жесткости

.

М_к.max = 28 кН×м (берем с эпюры М_к);

.

Приравнивая выражение для q_max и [q], получим:

,

откуда

м.

Из двух полученных значений d в качестве ответа берём больший (d = 0,142 м = 142 мм). Округляем его до ближайшего большего стандартного зна­че­ния: d = 150 мм.

5. Строим эпюру углов закручивания (рис. 36в).

Углы поворота сечений будем определять относительно сечения А, так как угол поворота этого сечения равен нулю. Углы пово­рота дру­гих сечений (В, C, D, E) равны сумме углов закручивания участков вала, расположенных между сечением А и сечением, угол за­кручи­вания которого определяется

.

Так как вал в этой задаче имеет один диаметр на всех участках, вы­числим I_k

м⁴.

Угол поворота сечения В равен углу закручивания участка АВ:

рад.

Угол поворота сечения С:

Угол поворота сечения D:

Угол поворота сечения Е:

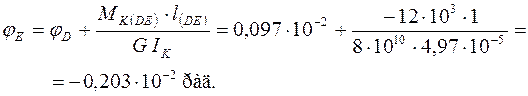
Откладывая от нулевой линии полученные значения углов по­ворота сечений в масштабе с учётом знака, а затем соединяя полу­ченные точки прямыми ли­ниями, получаем эпюру углов закручива­ния.

6. Вычисляем наибольшее касательное напряжение на наиболее нагру­женном участке вала.

Наиболее нагруженным является участок АВ, так как здесь наиболь­ший кру­тящий момент М_к(тах) = 28 кН×м.

Па =

=42,5 МПа.

7. Вычисляем наибольший относительный угол закручивания

рад/м.

 

Примечание. I_к был вычислен ранее на предыдущей странице.

 

Задача К 2.4

Эта задача является типичной задачей на определение необходи­мых разме­ров сечения из условия прочности. Её решение осуществ­ляет­ся в соответствии с алгоритмом решения этих задач (п. 4.2).

Угол поворота концевого сечения вала определяется так же, как угол пово­рота сечения Е в предыдущей задаче. Эпюра уг­лов закручивания не строится.

 

Задача К 2.5

Вычислить значения главных центральных моментов инерции, опре­делить положение главных центральных осей сечения (рис. 37).

Числовые данные: r = 0,2 a; l = 0,25 a; b = 0,75 a; h = a, а = 12см.

 

Решение

1. Вычерчиваем сечение в удобном масштабе.

2.Делим сечение на простые части: 1 – тре­угольник, 2 – полу­круг (мнимый).

3. Проводим начальные оси Х₀, У₀.

4. Готовим таблицу (табл. 13) для записи ре­зультатов расчета. Оп­ре­деляем коор­динаты центров тяжести со­ставляющих частей.

 

Примечание. В данном примере все расчеты выполнены в общем виде через а. Допускается, а иногда более удобно, выполнять расчеты в численном виде. Для этого на чертеже все размеры указывают в сантиметрах, затем их подставляют в рас­четные формулы, а ре­зультаты записывают в таблицу с соблюдением размерностей (см, см², см⁴).

 

Таблица 13

Часть	хс (а)	ус (а)	F (а2)	Ix (а4)	Iy (а4)	Ixy (а4)
I	0,25	0,333	0,375	0,0208	0,0117	-7,81×10 – 3
	0,0848	0,25	-0,0628	-6,29×10 – 4	-1,76×10 – 4
Сечение	0,283	0,35	0,312	0,0202	0,0115	-7,81×10 – 3

Окончание табл. 13

Часть	ai (а)	bi (а)	F (а4)	F (а4)	ai bi F (а4)
I	-0,017	-0,033	1,08×10 – 4	4,08×10 – 4	2,1×10 – 4
	-0,1	-0,198	-6,28×10 – 4	-2,46×10 – 3	-1,24×10 – 3
Сечение	---	---	-5,2×10 – 4	-2,05×10 – 3	-1,03×10 – 3

 

Треугольник ; .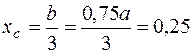

Полукруг ; .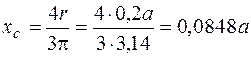

Заносим эти результаты в табл. 13. Наносим на чертеж положение центров тяжести треуголь­ника и полукруга, прово­дим через них центральные оси (х₁, у₁; х₂, у₂), парал­лельные началь­ным осям Х₀ У₀ (рис. 37).

Вычисляем и заносим в табл. 13 площади и мо­менты инерции со­ставляю­щих час­тей.

Треугольник

Примечание. Знак I_ху для треугольника и четверти круга зависит от положения относительно координатных осей.

 

	Рис. 37

Полукруг (мнимый):

;

;

;

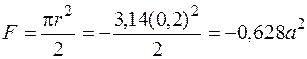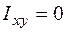, так как центральные оси полукруга являются его главными центральными осями, а относительно главных центральных осей I_ху = 0.

5. Вычисляем площадь сечения, для этого суммируем данные в столбце F, результат заносим в табл. 13.

.

Определяем координаты центра тяжести сечения и заносим резуль­таты в табл. 13:

;

.

Наносим на чертеж сечения положение центра тяжести и проводим через него центральные оси Х_сУ_с , параллельные начальным осям Х₀У₀.

Определяем a_i, b_i, F_i, F_i, a_i b_i F_i для простых частей, ре­зуль­таты заносим в табл. 13.

Треугольник

а₁ = у_с1 – у_с = 0,333 а – 0,35 а = - 0,017 а;

b₁ = х_с1 – х_с = 0,25 а – 0,283 а = - 0,033 а;

F₁ = (-0,017 а)²× 0,375 а² = 1,083×10 ^{– 4} а⁴;

F₁ = (-0,033 а)²× 0,375 а² = 4,083×10 ^{– 4} а⁴ ;

а₁b₁F₁ = (-0,017 а) (-0,033 а)×0,37 5 а² = 2,1×10 ^{– 4} а⁴.

Полукруг

a₂ = у_{с 2} – у_с = 0,25 а – 0,35 а = - 0,1 а;

b₂ = х_{с 2} – х_с = 0,0848 а – 0,283 а = - 0,198 а;

F₂ = (- 0,1 а)² (- 0,0628 а ²) = - 6,28×10 ^{– 4} а⁴;

F₂ = (- 0,198 а)² (0,0628 а ²) = - 2,46×10 ^{– 3} а⁴ ;

а₂b₂F₂ = (- 0,01 а) (- 0,198 а) (- 0,0628 а ²) = 1,24×10 ^{– 3} а⁴.

Определяем для сечения

S I_{x i} = 0,0208 a⁴ – 6,28×10 ^{– 4} а⁴ = 0,0202 а⁴;

S I_{y i} = 0,0117 a⁴ – 1,76×10 ^{– 4} а⁴ = 0,0115 а⁴;

S I_{x y i} = - 7,81×10 ^{– 4} a⁴ + 0 = -7,81×10 ^{– 4} а⁴;

S F_i = 1,08×10 ^{– 4} а⁴ – 6,28×10 ^{– 4} а⁴ = - 5,2×10 ^{– 4} а⁴;

S F_i = 4,08×10 ^{– 4} а⁴ – 2,46×10 ^{– 3} а⁴ = - 2,05×10 ^{– 3} а⁴;

S a_ib_i F_i= 2,1×10 ^{– 4} а⁴ – 1,24×10 ^{– 3} а⁴ = - 1,03×10 ^{– 3} а⁴.

Заносим результаты в табл. 13.

Определяем центральные моменты инерции I_x(с) , I_у(с) , I_xу(с) :

I_x(с) = S I_{x i} + S F_i = 0,0202 a⁴ – 5,2×10 ^{– 4} а⁴ = 0,0197 а⁴;

I_у(с) = S I_{y i} + S F_i = 0,0115 a⁴ – 2,05×10 ^{– 3} а⁴ = 0,00945 а⁴;

I_xу(с) = S I_{x y i} = S a_ib_i F_i = -7,81×10 ^{– 3} а⁴– 1,03×10 ^–3 а⁴= -8,84×10 ^–8 а⁴.

6. Определяем главные центральные моменты инерции сече­ния

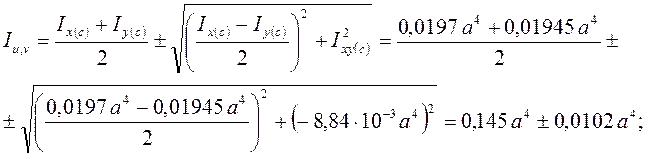
I_u = 0,0145 a⁴ + 0,0102 a⁴ = 0,0247 a⁴ = 0,0247×(0,12)⁴ = 512×10 ^{– 8}м⁴;

I_v = 0,014 5 a⁴ - 0,0102 a⁴ = 0,0043 a⁴ = 0,0043×(0,12)⁴ = 89,1×10 ^{– 8}м⁴.

 

Определяем угол a между осью Х_с и главной центральной осью u

= arctg (0,433) = 23,5°.

Через центр тяжести сечения под углом a к оси Х_с на чертеже прово­дим ось u и перпендикулярно к ней ось v.

 

Задача К 2.6

Вычислить значения главных центральных моментов инерции, оп­ре­делить положение главных центральных осей сложного сече­ния, со­ставленного из пла­стины 200´12 мм, швеллера № 20, двух равнобо­ких уголков № 8 (80´80´8) (рис. 38).

 

Решение

1. Вычерчиваем се­чение в удобном масштабе.

2. Делим сечение на прос­тые части: 1 – правый уголок, 2 – ле­вый уголок, 3 – швеллер, 4 – пла­стина.

3. Проводим на­чаль­ные оси Х₀, У₀. Так как сечение имеет верти­кальную ось симмет­рии, то ось У₀ на­правляем по оси симметрии, ось Х₀ – по границе меж­ду швеллером и угол­ками.

4. Готовим таб­лицу для записи ре­зульта­тов рас­чета (табл. 14).

Так как сечение имеет вер­тикальную ось симмет­рии, то центр тяжести его будет на­хо­диться на этой оси. Одна из главных цен­тральных осей будет совпадать с осью симметрии, другая будет проходить че­рез центр тяжести перпенди­кулярно оси симметрии. В свя­зи с этим данные столбцов I_xy и а_i b_i F_i для расчетов не потребуются и эти столбцы можно исключить из таб­лицы.

 

Таблица 14

Часть	хс, см	ус, см	Fi, см2	Ix, см 4	Iy, см 4	аi, см	bi, см	, см4	, см4
	2,87	2,27	12,3	73,36	73,36	-1,17	2,87	16,8
	-2,87	2,27	12.3	73,36	43,36	-1,17	-2,87	16,8
		-2,07	23,4			5,51
						6,56
Сечение		3,44				---	---

Для упрощения работы с числами все вычисления выполняем в см, см², см⁴.

Координаты центров тяжести вычисляем с учетом размеров час­тей и данных по положению центров тяжести уголка и швеллера в табли­цах сортамента по ГОСТ 8509-86 и ГОСТ 8240-72.

1 – уголок правый x_c = z₀+ 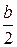= 2,27 + 0,6 = 2,87 см;

y_c = z₀ = 2,27 см.

2 – уголок левый x_c = - z₀ - 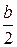= - 2,27 - 0,6 = - 2,87 см;

y_c = z₀ = 2,27 см.

3 – швеллер x_c = 0; y_c = - z₀ = - 2,07 см.

4 – полоса x_c = 0; y_c = 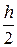= = 10 см.

Заносим эти данные в табл. 14. Через центры тяжести частей прово­дим их централь­ные оси, параллельные осям Х₀ У₀.

Площади и моменты инерции уголков и швеллера берем из таблиц сорта­мента и заносим в табл. 14. Для полосы вычисляем их по из­вест­ным формулам

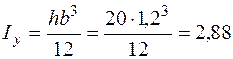F = bh = 1,2×20 = 24 см²; см⁴;

см⁴.

Определяем площадь сечения

F = F_i = 12,3 + 12,3 + 23,4 + 24 = 72 см².

Определяем координаты центра тяжести сечения. Так как ось У₀ яв­ляется осью симметрии и центр тяжести находится на этой оси, то x_c = 0

= 3,44 см.

Через центр тяжести сечения проводим центральные оси Х_с У_с. Опре­деляем a_i, b_i, F_i, F_i.

1 – уголок правый:

а₁ = у_с1 – у_с = 2,27 – 3,44 = - 1,17 см;

b₁ = х_с1 – х_с = 2,87 – 0 = 2,87 см;

F₁ = (-1,17)²× 12,3 = 16,8 см⁴;

F₁ = 2,87²× 12,3 = 101 см⁴.

2 – уголок левый:

а₂ = у_с1 – у_с = 2,27 – 3,44 = - 1,17 см;

b₂ = х_с1 – х_с = - 2,87 – 0 = - 2,87 см;

F₂ = (-1,17)²× 12,3 = 16,8 см⁴;

F₂ = (-2,87)²× 12,3 = 101 см⁴.

3 – швеллер:

а₃ = у_с3 – у_с = -2,07 – 3,44 = - 5,57 см;

b₃ = х_с3 – х_с = 0 – 0 = 0 см;

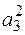F₃ = (- 5,57)²× 23,4 = 710 см⁴;

F₃ = 0.

4 – полоса:

а₄ = у_с4 – у_с = 10 – 3,44 = 6,56 см;

b₄ = х_с4 – х_с = 0 – 0 = 0 см;

F₄ = 6,56²× 24 = 1032 см⁴;

F₄ = 0.

Заносим результаты вычислений в табл. 14.

Вычисляем

S I_{x i} = 73,36 + 73,36 + 113 + 800 = 1060 см⁴;

S I_{y i} = 73,36 + 73,36 + 1520 + 2,88 = 1670 см⁴;

S F_i = 16,8 + 16,8 + 710 + 1032 = 1775 см⁴;

S F_i = 101 + 100 = 202 см⁴.

Вычисляем

I_x(с) = S I_{x i} + S F_i = 1060 + 1775 = 2835 см⁴;

I_у(с) = S I_{y i} + S F_i = 1670 + 202 = 1872 см⁴.

 

5. Так как сечение имеет ось симметрии, то главная центральная ось U совпадает с осью Х_с, главная центральная ось V – с осью У_с.

I_u = I_x(c) = 2835 см⁴ = 2835×10^-8 м⁴;

I_v = I_у(c) = 1872 см⁴ = 1872×10^-8 м⁴.

 

Поделиться:

Воспользуйтесь поиском по сайту: